Центр тяжести – это точка, в которой сосредоточена масса тела. Нахождение центра тяжести является важным этапом при проектировании и расчете конструкций. Швеллер – это сварной прокатный профиль, который широко используется в строительстве для создания различных металлических конструкций. Для определения точного положения центра тяжести швеллера существует специальная формула.
Формула нахождения центра тяжести швеллера состоит из нескольких этапов. В первую очередь необходимо разделить швеллер на простые геометрические фигуры, такие как прямоугольники и треугольники. Затем необходимо найти площади этих фигур, а также их центры тяжести. После этого проводится дополнительные расчеты для определения положения центра тяжести всего швеллера.
Примеры расчетов центра тяжести швеллера могут помочь лучше понять принцип работы формулы. Для примера возьмем швеллер с размерами 100х50 мм и длиной 6 м. Сначала разобьем его на прямоугольники и треугольники, найдем их площади и центры тяжести. Затем проведем расчеты для определения положения центра тяжести всего швеллера.
Основы и примеры расчетов центра тяжести швеллера
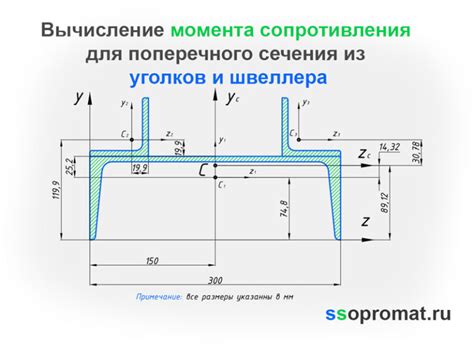
Центр тяжести швеллера – это геометрическая точка, в которой можно считать сосредоточенным всю массу данного профиля. Расчет этой точки является важным этапом проектирования и расчета различных конструкций, содержащих швеллеры. Ее положение зависит от геометрических параметров сечения швеллера и его материала.
Формула для нахождения центра тяжести швеллера представляет собой интеграл, который учитывает площадь и координаты каждого элементарного поперечного сечения профиля в расчетной плоскости. Данная формула включает операции вычисления интегралов и арифметические операции и позволяет определить координаты центра тяжести вдоль осей x и y.
Рассмотрим пример расчета центра тяжести швеллера. Пусть имеется швеллер с поперечным сечением в форме буквы "С". Площадь сечения можно разделить на два прямоугольника и один треугольник. Для каждой фигуры находим момент относительно осей x и y, затем находим сумму моментов, после чего делим полученные значения на сумму площадей фигур. Полученные значения будут являться координатами центра тяжести швеллера.
Из данного примера видно, что расчет центра тяжести швеллера требует отдельного анализа поперечного сечения и вычисления моментов инерции и площадей различных фигур. Важно учитывать, что формула для расчета центра тяжести может меняться в зависимости от геометрических параметров швеллера. Правильное определение центра тяжести швеллера способствует его надежности и устойчивости в конструкциях, где он используется.
Что представляет собой швеллер и зачем нужен его расчет?

Швеллер - это стальной профиль, имеющий форму буквы "Ш". Он широко используется в строительстве и машиностроении для создания различных конструкций, таких как балки, рамы и фермы. Основными преимуществами швеллера являются его прочность и жесткость.
Расчет центра тяжести швеллера является важным этапом при проектировании и строительстве конструкций, в которых он будет использоваться. Центр тяжести, или центр массы, определяет точку, в которой можно считать сосредоточенной вся масса швеллера. Знание этой точки позволяет правильно распределить нагрузку и спроектировать конструкцию таким образом, чтобы она оставалась устойчивой и не подвергалась деформации при работе.
Расчет центра тяжести швеллера основан на геометрических параметрах профиля, таких как высота, ширина и толщина стенок. Для расчета часто используют различные формулы и таблицы. Есть несколько способов определения центра тяжести швеллера, включая графический метод, аналитический метод и использование специальных программных средств.
Правильный расчет центра тяжести швеллера является ключевым моментом для обеспечения безопасности и надежности конструкций, в которых он используется. Он позволяет инженерам и дизайнерам оптимизировать конструкцию, учитывая особенности нагрузок и требования к прочности. Такой расчет также позволяет сэкономить материалы и снизить стоимость проекта, что важно при масштабных строительных работах.
Формула нахождения центра тяжести швеллера: шаги расчета и символы
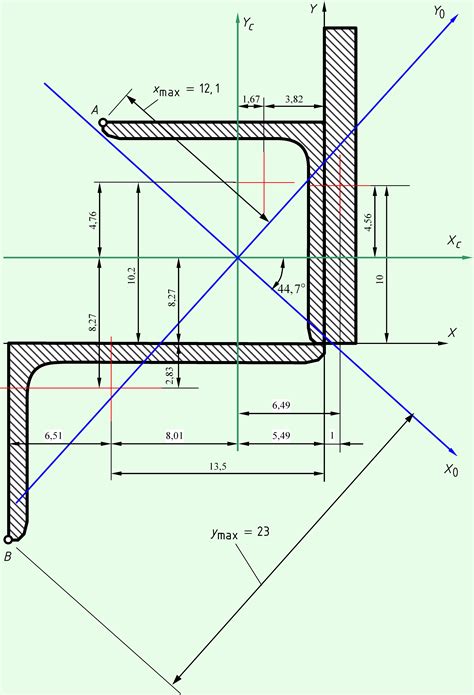
Швеллер - это один из видов металлических профилей, используемых в строительстве для создания несущих конструкций. Он имеет форму буквы "Ш" и состоит из вертикальной стенки (называемой стенкой поперечным сечением) и двух горизонтальных палок. Для правильного расчета прочности и стабильности конструкции важно знать положение центра тяжести швеллера.
Формула для нахождения центра тяжести швеллера состоит из нескольких шагов. Сначала необходимо вычислить площадь поперечного сечения швеллера, которую обозначим как S. Затем найдем площадь p-го элемента поперечного сечения, обозначим ее как Sp, и расстояние от этого элемента до оси OX, обозначим как xp. Далее, умножим площадь каждого элемента на его координату и сложим результаты для всех элементов. И, наконец, поделим полученную сумму на общую площадь поперечного сечения швеллера, чтобы найти координату центра тяжести по оси OX.
Символы, используемые в формуле нахождения центра тяжести швеллера:
- S - площадь поперечного сечения швеллера;
- Sp - площадь p-го элемента поперечного сечения швеллера;
- xp - расстояние от p-го элемента до оси OX;
- x̅ - координата центра тяжести швеллера по оси OX;
- n - количество элементов поперечного сечения.
Правильный расчет центра тяжести швеллера позволяет оптимизировать конструкцию, обеспечивая ее прочность и стабильность. Знание основ расчета и символов, используемых в формуле, является важным для инженеров и строителей.
Примеры расчета центра тяжести швеллера с пояснениями
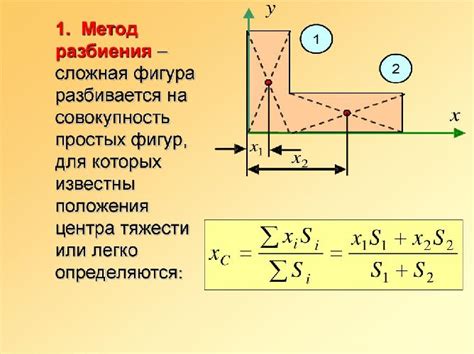
Расчет центра тяжести швеллера является важной задачей при проектировании и строительстве различных конструкций. Для выполнения расчетов необходимо знать геометрические параметры швеллера, такие как ширина полки, высота швеллера, толщина полки и стенки.
Примером расчета может служить случай, когда швеллер имеет ширину полки 120 мм, высоту 200 мм, толщину полки 10 мм и стенки 7 мм.
Для нахождения центра тяжести необходимо сначала вычислить площадь каждой полки и стенки, умножив соответствующие геометрические параметры их толщиной. Далее, найденные площади нужно умножить на расстояние от их центра до оси симметрии швеллера.
В данном примере расчета центра тяжести для швеллера с указанными параметрами площади полок составят 1200 кв.мм, площадь стенок - 980 кв.мм. Расстояние от центра полок до оси симметрии равно 35 мм, а от центра стенок - 60 мм. Соответствующие значения перемножаем и получаем 42000 куб.мм*мм для полок и 58800 куб.мм*мм для стенок.
Далее, найдем сумму всех полученных значений и разделим ее на площадь всего сечения швеллера. В результате получим координаты центра тяжести относительно одной из осей.
В данном примере расчета центра тяжести для швеллера его координаты будут 55 мм и 105 мм относительно оси X и Y соответственно. Таким образом, можно определить точку приложения силы и обеспечить необходимое равновесие конструкции.
Вопрос-ответ

Какая формула используется для нахождения центра тяжести швеллера?
Для нахождения центра тяжести швеллера воспользуйтесь следующей формулой: x = (A1*x1 + A2*x2 + ... + An*xn) / (A1 + A2 + ... + An), где x - координата центра тяжести по оси, A - площадь части швеллера, x - координата этой части швеллера.
Как можно посчитать центр тяжести швеллера на практике?
Для расчета центра тяжести швеллера на практике необходимо разделить конструкцию швеллера на несколько простых элементов, вычислить их площади и координаты центров тяжести, а затем воспользоваться формулой x = (A1*x1 + A2*x2 + ... + An*xn) / (A1 + A2 + ... + An).
