Гибка металла – это процесс деформации материала, при котором он изгибается без образования трещин или разрывов. Для успешного выполнения гибки металла необходимо знание основных формул, с помощью которых можно рассчитать необходимую силу, а также угол изгиба и радиус гибки. В данной статье рассмотрим основные формулы, которые используются при гибке металла.
Первая основная формула – это формула расчета силы при гибке металла. Сила, необходимая для гибки, зависит от различных факторов, включая тип и толщину материала, длину и ширину изгибаемой детали, а также радиус гибки. Формула расчета силы имеет вид: F = k * S * R, где F – сила гибки, k – коэффициент, зависящий от типа материала и шероховатости поверхности, S – площадь поперечного сечения, R – радиус гибки.
Вторая формула – это формула расчета угла изгиба. Угол изгиба определяет степень загиба материала. Он также зависит от типа и толщины материала, а также от радиуса гибки. Формула расчета угла изгиба имеет вид: α = 180 * L / (π * R), где α – угол изгиба в градусах, L – длина изгибаемой детали, R – радиус гибки.
Корректный расчет необходимых параметров при гибке металла позволяет обеспечить качественное выполнение данной операции и минимизировать возможные дефекты и повреждения материала. Основные формулы, описанные в данной статье, помогут вам осуществить точные расчеты и достичь необходимых результатов.
Основные формулы гибки металла
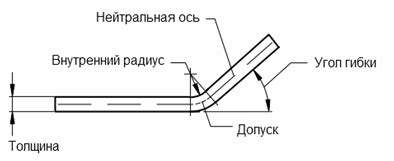
Гибка металла - процесс, при котором детали из металла приобретают желаемую форму, согласно заданным параметрам и углам гиба. Для успешного выполнения гибки металла необходимо знать основные формулы, которые используются при расчете изгиба деталей.
Одной из основных формул при гибке металла является радиус изгиба. Радиус изгиба (R) определяет характеристику изгиба детали и зависит от толщины материала (t), угла гиба (α) и ее ширины (W). Формула для расчета радиуса изгиба: R = K * t, где K - коэффициент, который зависит от характеристик материала и процесса гибки.
Также при гибке металла используется формула для расчета длины изгиба детали. Длина изгиба (L) определяет протяженность изгибаемой области. Для расчета длины изгиба используется следующая формула: L = π * R * α / 180, где π - математическая константа (пи).
Дополнительно, при гибке сложных деталей, может использоваться формула для расчета пути изгиба. Путь изгиба (S) представляет собой длину, которую проходит край внешней поверхности детали при изгибе. Формула для расчета пути изгиба: S = 2 * R * α / 180 + L, где S - путь изгиба, R - радиус изгиба, α - угол гиба, L - длина изгиба.
Знание основных формул при гибке металла является важным фактором для успешной реализации процесса. Они позволяют корректно расчитать радиус изгиба, длину изгиба и путь изгиба, что обеспечивает точность и качество готовой детали.
Формулы для расчета радиуса изгиба
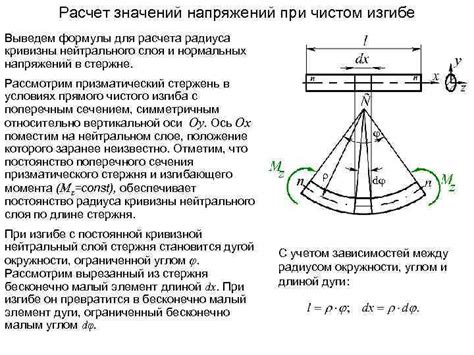
Радиус изгиба является важным параметром при гибке металла и определяет минимальную кривизну, которую можно получить при изгибе материала. Формулы для расчета радиуса изгиба зависят от различных факторов, таких как тип материала, его толщина и свойства металла.
Для изгиба металла с прямоугольным сечением можно использовать формулу:
Радиус изгиба (R) = (t * k) / (6 * a)
Для расчета радиуса изгиба металла с круглым сечением применяется следующая формула:
Радиус изгиба (R) = 2 * t * k / a
Коэффициент изгиба (k) зависит от различных условий гибки и свойств материала. Обычно он вычисляется эмпирически на основе опыта или устанавливается на основе данных от производителя оборудования для гибки металла.
При использовании данных формул для расчета радиуса изгиба необходимо учитывать, что эти формулы являются лишь приближенными и могут отличаться в зависимости от конкретных условий и свойств материала.
Формулы для определения длины развертки
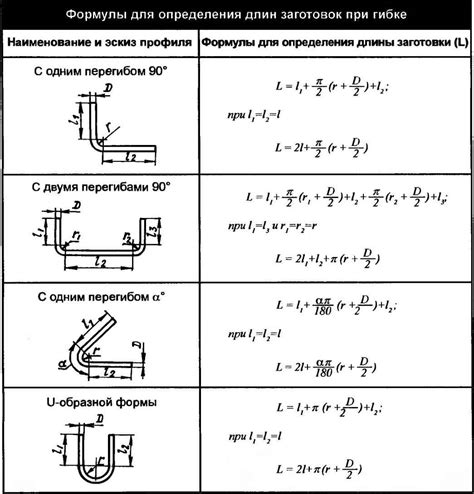
Длина развертки – это длина поверхности, которую описывает материал металла при его гибке для создания требуемой формы или изгиба.
Существует несколько формул, позволяющих определить длину развертки в зависимости от различных факторов, таких как радиус гибки, толщина материала и угол гибки:
- Формула для простого изгиба: L = π * (r + (t / 2))
- Формула для изгиба на широкой штамповке с малым радиусом: L = π * (r + (t / 2)) * (1 + (r / t))
- Формула для изгиба на узкой штамповке с малым радиусом: L = π * (r + (t / 2)) * (1 + (2 * r / t))
Где L – длина развертки, r – радиус гибки, t – толщина материала.
Определение длины развертки является важным этапом при гибке металла, поскольку она позволяет предварительно расчитать необходимую длину материала и учесть возможные деформации при гибке. Это позволяет снизить количество отходов и обеспечить более эффективное использование материала.
Формулы для расчета усилия при гибке
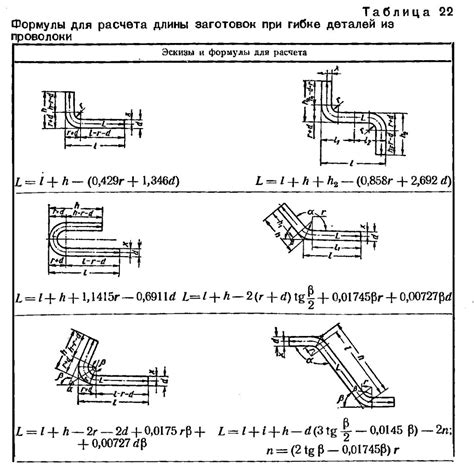
При гибке металла возникают определенные усилия, которые необходимо учитывать при проектировании и расчете деталей. Знание основных формул позволяет предвидеть и оптимизировать процесс гибки.
Одной из основных формул, используемых при расчете усилия при гибке, является формула Максвелла. По этой формуле можно определить максимальное усилие, которое будет испытывать материал при гибке. Формула Максвелла представляет собой соотношение между моментом силы и изменением угла изгиба.
Еще одной важной формулой, используемой при расчете усилия при гибке, является формула Планшера. Она позволяет определить необходимый радиус изгиба для того, чтобы предотвратить возникновение разрушений или деформаций в материале. Формула Планшера учитывает такие факторы, как прочность материала и его свойства при гибке.
Для расчета усилия при гибке также можно использовать табличные данные, которые учитывают конкретные характеристики материала и размеры детали. В таких таблицах приведены значения усилий для различных материалов и размеров деталей.
Однако при расчете усилия при гибке необходимо учитывать не только формулы, но и такие параметры, как толщина материала, длина изгиба, угол изгиба и другие. Все эти параметры влияют на результат расчета и точность полученных значений. Поэтому при проектировании и расчете деталей необходимо учитывать все факторы и выполнять необходимые расчеты.
Формулы для определения толщины листа

При гибке металлической листовой заготовки одним из важнейших параметров, который нужно учесть, является толщина листа. Знание точной толщины листа позволяет определить, какую силу нужно применить при гибке и какой радиус изгиба выбрать.
Существует несколько формул для определения толщины листа. Одна из наиболее распространенных формул - это формула Юнгера:
- Для одинарного листа:
- t = l ÷ 2 × n
- t = l ÷ n
Где t - толщина листа, l - длина заготовки, n - количество изгибов.
Также существует формула расчета толщины листа по гипотенузе треугольника, образованного изделием и изгибной пластиной:
t = s × sin(α) + r × (1 - cos(α))
Где t - толщина листа, s - длина стороны треугольника, α - угол наклона изгибной пластины, r - радиус изгиба.
Зная толщину листа, можно выбрать оптимальные параметры для гибки металла и обеспечить высокое качество изготовления деталей.
Формулы для расчета длины загиба
При гибке металла часто требуется знать длину загиба, чтобы правильно выполнить операцию гибки и изготовить нужную деталь. Для расчета длины загиба существуют специальные формулы, которые позволяют определить этот параметр.
Простейшей формулой для расчета длины загиба является формула с учетом радиуса гиба и угла загиба. Длина загиба (L) может быть рассчитана по формуле: L = 3,14 * R * (Угол загиба / 180), где R - радиус гиба, а Угол загиба - угол, на который происходит загиб детали.
Если известны ширина детали (W), радиус гиба (R) и угол загиба (Угол загиба), то можно воспользоваться формулой: L = R * (Угол загиба / 90) + (W / 2 * tg(Угол загиба / 2)), где tg - тангенс. Эта формула позволяет учесть ширину детали при расчете длины загиба.
Для более сложных случаев, когда загиб детали имеет нестандартную форму, можно воспользоваться таблицей, в которой указаны значения длины загиба для различных комбинаций радиуса гиба и угла загиба. Такая таблица облегчает процесс расчета длины загиба и позволяет получить более точные значения для конкретных случаев.
Важно помнить, что формулы и таблицы для расчета длины загиба являются приближенными и могут иметь ограничения в использовании для разных материалов и конструктивных особенностей. Поэтому рекомендуется всегда проверять полученные результаты на практике и корректировать их при необходимости, чтобы обеспечить точность и качество гибки металла.
Формулы для определения угла изгиба

Угол изгиба – это угол, образованный двумя линиями, на которых происходит изгиб металла. Этот параметр имеет большое значение при гибке металла, так как он определяет градус изгиба и, следовательно, функциональность изделия.
Для определения угла изгиба используются следующие формулы:
- Угол изгиба в градусах рассчитывается по формуле:
Угол изгиба = Арктангенс (сторона А / сторона В)
- Угол изгиба в радианах можно найти, поделив угол изгиба в градусах на 57,3.
Такие формулы позволяют точно определить угол изгиба металлической детали и осуществить гибку с нужной точностью. Кроме того, при использовании гибочного оборудования, на основе этих формул можно программно задавать нужные параметры гибки и получать идеальные результаты.
Формулы для расчета радиуса загиба
При гибке металла, для определения радиуса загиба часто используются следующие формулы:
- Формула для расчета радиуса загиба методом самого короткого расстояния: R = K * t, где R - радиус загиба, K - коэффициент, зависящий от типа материала и его толщины, t - толщина листа.
- Формула для расчета радиуса загиба методом минимального радиуса R = 0.5 * K * t, где R - радиус загиба, K - коэффициент, зависящий от типа материала и его толщины, t - толщина листа.
- Формула для расчета радиуса загиба методом подбора R = L / (2 * π), где R - радиус загиба, L - длина загибаемой части.
Для точного определения радиуса загиба необходимо учитывать не только тип материала и его толщину, но и другие факторы, такие как радиус гибки, угол гибки, качество поверхности и т. д. Поэтому в некоторых случаях может потребоваться проведение дополнительных расчетов или экспериментов.
Важно помнить, что формулы для расчета радиуса загиба являются лишь приближенными и предоставляют общую оценку. Практическое определение радиуса загиба лучше проводить на основе опыта, используя стандартные инструменты и оборудование для гибки металла.
Вопрос-ответ

Какие основные формулы используются при гибке металла?
Основные формулы при гибке металла включают формулу для расчета радиуса гиба, формулу для определения угла гиба и формулу для расчета силы гиба. Эти формулы позволяют определить необходимые параметры для выполнения гибочных операций.
Какая формула используется для расчета радиуса гиба металла?
Формула для расчета радиуса гиба металла зависит от толщины и свойств материала. Одна из наиболее распространенных формул для расчета радиуса гиба металла - это формула Тейлора, которая использует следующее выражение: R = K * t, где R - радиус гиба, t - толщина материала, K - коэффициент, зависящий от материала и других параметров.
Как определить угол гиба металла?
Угол гиба металла можно определить с помощью формулы, которая учитывает толщину материала и радиус гиба. Для прямоугольного материала угол гиба можно рассчитать по следующей формуле: α = (180 * t) / (π * R), где α - угол гиба, t - толщина материала, R - радиус гиба. Для других форм материала существуют другие формулы для расчета угла гиба.
Как рассчитать силу гиба металла?
Сила гиба металла зависит от нескольких факторов, таких как толщина материала, его прочностные характеристики, а также радиус и угол гиба. Для расчета силы гиба можно использовать следующую формулу: F = K * t * L, где F - сила гиба, K - коэффициент, зависящий от материала и геометрии заготовки, t - толщина материала, L - длина заготовки.
Есть ли альтернативные формулы при гибке металла?
Да, существует несколько альтернативных формул, которые могут быть использованы при гибке металла в зависимости от конкретных условий и требований процесса. Некоторые из них могут учитывать дополнительные факторы, такие как упругость материала, его пластичность и т. д. Однако основные формулы, которые были упомянуты ранее, являются базовыми и широко используются в практике гибки металла.
