Математика и металлургия - две науки, на первый взгляд совершенно разные. Одна изучает абстрактные числа и формулы, другая - свойства различных металлов и их применение в промышленности. Однако, эти две области неожиданно пересекаются друг с другом и способны вместе решать насущные проблемы, связанные с производством и использованием металлов.
Одной из важных задач, решаемых математическими методами в металлургии, является расчет структуры и свойств материалов. Математика позволяет предсказывать и оптимизировать химический состав сплавов, интерактивно моделировать свойства металлических пластин и прочности строительных конструкций. С помощью различных математических методов и моделей, инженеры могут проанализировать и оптимизировать процессы обработки и получения металлов, чтобы повысить их качество и эффективность.
Еще одним интересным направлением исследований является математическое моделирование экономических и социальных проблем, связанных с производством и использованием металлов. Математическое моделирование позволяет предсказывать спрос на металлы в будущем, а также оптимизировать производственные процессы и прогнозировать возможные экономические последствия.
Математика и металлургия - это далеко не всеобъемлющая связь, которая проявляется не только в математическом моделировании свойств материалов и оптимизации производства, но также в разработке и использовании новых математических методов для решения металлургических задач. Такое сотрудничество между науками открывает новые перспективы для улучшения и инноваций в металлургической промышленности и ведет к созданию новых материалов, более прочных и устойчивых к деформациям и коррозии.
Таким образом, совместные усилия математиков и металлургов позволяют не только решать конкретные задачи, связанные с производством и использованием металлов, но и содействовать развитию науки и технологий, а также находить новые сферы применения металлов в инженерии и строительстве. Математика в мире металлов - это не просто расчеты и прогнозы, это сотрудничество науки и промышленности для достижения общих целей.
Роль математики в научных исследованиях

Математика играет важную роль в научных исследованиях, включая изучение металлов. Она является ключевым инструментом для анализа данных и воссоздания сложных физических процессов.
Моделирование – один из основных методов, используемых в математике для исследования металлов. Математические модели позволяют ученым предсказывать поведение материалов в различных условиях и оптимизировать процессы производства.
Статистический анализ данных играет также важную роль в научных исследованиях металлов. С помощью статистических методов ученые могут выявить закономерности в полученных данных и вывести статистические законы, которые помогают более точно предсказывать свойства материалов.
Оптимизация – это еще одно направление, где математика играет решающую роль. Математические методы позволяют найти оптимальные параметры производства и дизайна металлических изделий, что позволяет повысить их качество и эффективность.
Кроме того, математические методы применяются для моделирования тепловых и механических процессов, связанных с производством и свойствами металлов. Такое моделирование позволяет проводить виртуальные эксперименты, что снижает затраты на физические испытания и ускоряет разработку новых материалов и технологий.
В итоге, математика играет фундаментальную роль в научных исследованиях, связанных с металлами. Она позволяет ученым предсказывать, анализировать и оптимизировать свойства материалов, что способствует развитию современной металлургии и промышленности в целом.
Математические модели в изучении свойств металлов
Математические модели представляют собой основной инструмент для исследования свойств металлов. Они позволяют ученым проводить расчеты и прогнозировать различные характеристики металлических материалов, такие как прочность, пластичность, теплопроводность и т.д.
Одной из самых распространенных математических моделей в изучении металлов является модель деформации. Она основана на законах механики и позволяет предсказывать поведение металла при различных условиях нагружения.
Также математические модели применяются для изучения структуры металлических материалов. Они позволяют описать распределение атомов, дефектов и микроструктур в металле, что в свою очередь позволяет предсказать его свойства.
Важной областью применения математических моделей в изучении свойств металлов является моделирование термических процессов. С их помощью можно расчитать распределение температуры и скорость охлаждения металла, что имеет большое значение при проектировании и производстве металлических изделий.
Использование математических моделей в изучении свойств металлов позволяет значительно ускорить процесс исследования и получить более точные результаты. Они являются неотъемлемой частью современной материаловедении и позволяют ученым и инженерам создавать новые материалы с улучшенными свойствами.
Расчеты и прогнозы свойств металлов

Расчеты и прогнозы свойств металлов являются важным этапом в изучении и применении математики в мире металлургии. С помощью математических моделей и методов можно предсказать механические, электромагнитные, химические и другие свойства различных металлических материалов.
Одним из основных направлений в расчетах свойств металлов является моделирование микроструктурных процессов. С помощью моделей структурных превращений металлов можно предсказать изменение их фазового состава, механических свойств и структуры при различных загрузках, температурах и времени действия нагрузки.
Также математические модели используются для расчета термодинамических свойств металлов, таких как температурная зависимость плотности, теплоемкости и теплопроводности. Эти расчеты позволяют оптимизировать процессы нагрева и охлаждения металлов в металлургической промышленности.
Немалую роль играют и математические модели при расчете механических свойств металлов, таких как прочность, упругость, пластичность и усталостность. С их помощью можно определить оптимальные параметры сплавов, чтобы обеспечить требуемые механические свойства металлических изделий.
Кроме того, с помощью математических моделей возможно прогнозирование коррозионного поведения металлов и сплавов. Это позволяет разрабатывать новые материалы, обладающие высокой стойкостью к агрессивной среде и улучшая качество и срок службы металлических конструкций.
Применение математики в создании новых материалов

Математика играет важную роль в процессе разработки и создания новых материалов. Она позволяет инженерам и научным работникам проводить расчеты и моделирование свойств материалов, оптимизировать их структуру и свойства.
Одним из основных применений математики в создании новых материалов является численное моделирование. С помощью математических моделей и вычислительных методов можно предсказывать и анализировать процессы в материалах на молекулярном уровне.
Также математика используется для оптимизации структуры материалов, а именно для выбора оптимальных пропорций компонентов, расчета тепло- и массообмена, анализа напряженно-деформированного состояния материалов при различных условиях эксплуатации.
Математические методы позволяют также проводить сравнительный анализ различных вариантов материалов, с учетом их физических и механических свойств. Они позволяют выбрать самый оптимальный вариант, учитывая заданные критерии.
Искусственный интеллект и машинное обучение также находят применение в создании новых материалов. Благодаря математическим алгоритмам и моделям, можно проанализировать большой объем данных и найти зависимости, которые помогут оптимизировать процесс создания и улучшения материалов.
Методы прогнозирования свойств металлов
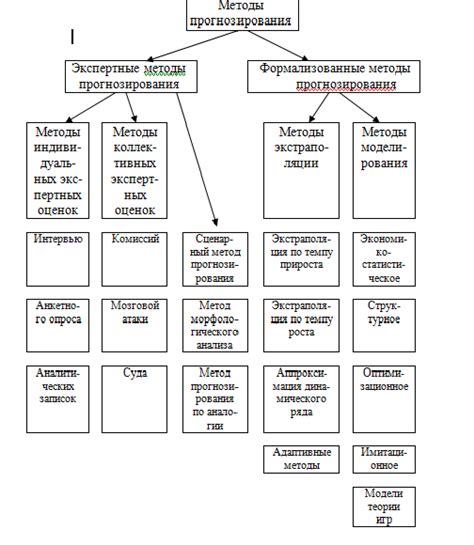
Прогнозирование свойств металлов является важной задачей в мире материаловедения и металлургии. Существует несколько методов и подходов, которые позволяют предсказывать различные свойства металлов, такие как механическая прочность, электропроводность или термическая устойчивость.
Один из методов прогнозирования свойств металлов - использование математических моделей. Математические модели позволяют описывать поведение металла в различных условиях и на основе этих моделей делать предсказания о его свойствах. Например, модели могут учитывать состав металла, его структуру, тепловую обработку и другие факторы, которые могут влиять на его свойства.
Другой метод прогнозирования свойств металлов - использование компьютерного моделирования. Компьютерное моделирование позволяет создавать виртуальные модели металлов и проводить различные эксперименты без необходимости физического создания и испытания реальных образцов. Это позволяет сократить время и затраты на исследование и предсказывать свойства металлов на основе моделирования.
Ещё один метод прогнозирования свойств металлов - использование исторических данных и статистических методов. Анализ данных о свойствах металлов в прошлом позволяет выявить закономерности и тренды, которые можно использовать для предсказания свойств металлов в будущем. Например, можно использовать статистические модели, такие как регрессионный анализ, для предсказания механической прочности металлов на основе их состава и структуры.
В зависимости от конкретной задачи и доступных данных, исследователи выбирают подходящий метод для прогнозирования свойств металлов. Часто комбинируют несколько методов для достижения наилучших результатов.
Применение математических алгоритмов в металлургии

Металлургия - это область науки и техники, изучающая процессы производства и обработки металлов. В последние годы применение математических алгоритмов в металлургии стало неотъемлемой частью процесса производства и оптимизации работы металлургических предприятий.
Математические алгоритмы позволяют проводить расчеты и прогнозирование различных параметров и свойств металлов, что помогает повысить качество и эффективность производства. Например, с помощью алгоритмов можно определить оптимальные параметры температуры и скорости нагрева для получения заданных свойств металла.
Одним из самых распространенных алгоритмов, применяемых в металлургии, является метод конечных элементов. С помощью этого метода можно проводить сложные расчеты напряжений, деформаций и теплового поля в металлических конструкциях и отливках. Это позволяет оптимизировать дизайн и производственные процессы.
Кроме того, математические алгоритмы применяются для анализа и прогнозирования поведения металла в различных условиях эксплуатации. Например, с помощью алгоритмов можно определить срок службы металлической конструкции, учитывая воздействие факторов окружающей среды, нагрузок и коррозии.
Также математические алгоритмы находят применение в определении оптимальных параметров смешивания различных металлических сплавов. С их помощью можно определить процентное содержание каждого компонента для достижения требуемых свойств и качественных характеристик готового сплава.
В целом, применение математических алгоритмов в металлургии позволяет повысить эффективность производства и снизить потери, сделав процессы более точными и контролируемыми.
Вопрос-ответ

Зачем нужны математические модели в металлургии?
Математические модели в металлургии позволяют проводить расчеты и прогнозировать различные параметры и свойства металлов. Они помогают оптимизировать процессы производства, улучшить качество и экономическую эффективность производства металлов.
Какие математические методы используются в металлургии?
В металлургии используются различные математические методы, такие как термодинамические моделирование, моделирование механического поведения металлов, численное моделирование процессов литья и прокатки, статистический анализ данных и многие другие.
