Параллелограмм - это фигура, у которой противоположные стороны равны и параллельны. Он известен своими свойствами и особенностями, которые позволяют решать различные математические задачи. Более того, существует целых 408 доказательств того, что параллелограмм может быть ромбом.
Чтобы доказать, что параллелограмм является ромбом, необходимо удостовериться, что все его стороны равны. Ромб - это параллелограмм, у которого все стороны равны. Это свойство делает его особенным и интересным для изучения.
Существует множество способов доказать, что параллелограмм является ромбом. Какие именно из 408 доказательств вы выберете, зависит от ваших предпочтений и возможностей. Важно помнить, что математика - это точная наука, и каждое утверждение нуждается в строгом доказательстве.
Критерии равенства сторон
Таким образом, критерием равенства сторон в параллелограмме, который является ромбом, является равенство всех четырех сторон друг другу.
Диагонали равны равным сторонам
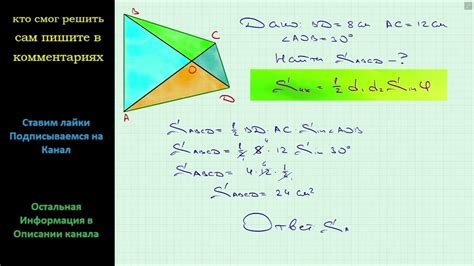
В ромбе диагонали ромба образуют перпендикуляр, и точка их пересечения делит каждую диагональ на две равные части. Таким образом, если стороны ромба равны друг другу, то и диагонали также будут равными, и каждая из них будет разделена на две равные части точкой их пересечения.
Угловые диагонали
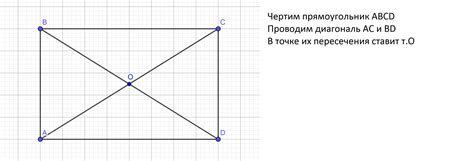
Пусть у нас есть параллелограмм ABCD. Рассмотрим угловую диагональ AC. Она делит параллелограмм на два треугольника: △ABC и △ADC. Так как у параллелограмма противоположные стороны равны, то AB = CD и BC = AD. Также у параллелограмма противоположные углы равны, поэтому угол BAC = угол CDA и угол ABC = угол ADC. Из этого следует, что треугольники △ABC и △ADC равны по двум сторонам и углу между ними, что означает, что угловая диагональ AC делит параллелограмм на два равных треугольника.
Аналогично, угловая диагональ BD также делит параллелограмм на два треугольника, которые также равны по двум сторонам и углу между ними. Таким образом, параллелограмм ABCD можно разбить на четыре равных треугольника △ABC, △ADC, △CDA и △CDB.
Углы между диагоналями равны
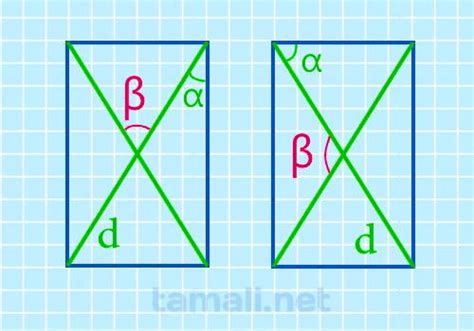
Для параллелограмма верно утверждение о том, что углы между его диагоналями равны.
Это следует из того, что диагонали параллелограмма делят его на два равных треугольника. Углы противоположного параллельного, а значит, также противоположного равных сторон треугольника равны. Таким образом, углы между диагоналями параллелограмма также равны.
Сохранение параллельности
Если у нас есть параллелограмм, то по его определению противоположные стороны параллельны. Но для ромба это не достаточно. Нам также необходимо убедиться, что все его стороны равны друг другу.
Для этого взглянем на параллелограмм. Отметим, что диагонали параллелограмма делят его на два равных треугольника. Из свойств треугольника следует, что противоположные стороны равны, а значит, и все стороны равны по определению. Таким образом, мы получаем, что параллелограмм является ромбом.
Диагонали пересекаются под прямым углом

Вопрос-ответ

Какие свойства параллелограмма позволяют доказать, что он является ромбом?
Для доказательства того, что параллелограмм является ромбом, необходимо учесть следующие свойства: параллельные стороны параллелограмма равны и смежные стороны параллелограмма равны. Это позволяет утверждать, что если все стороны параллелограмма равны, то он является ромбом.
Как можно понять, что параллелограмм представляет собой ромб?
Для того чтобы понять, что параллелограмм является ромбом, достаточно проверить выполнение следующих условий: все стороны параллелограмма равны между собой, а также углы между соответствующими сторонами равны 90°. Если все эти условия выполняются, то параллелограмм можно с уверенностью назвать ромбом.



