Алгебраическая дробь - это одно из ключевых понятий алгебры, которое используется для работы с алгебраическими выражениями. Алгебраическая дробь представляет собой дробное выражение, в котором числитель и знаменатель могут быть алгебраическими выражениями, а не только числами.
Сложность алгебраических дробей заключается в том, что их не всегда можно упростить или выразить одним дробным числом. Для упрощения алгебраической дроби используются правила операций с дробями и алгебраическими выражениями.
Понимание основных принципов работы с алгебраическими дробями позволяет эффективно решать сложные уравнения и задачи, связанные с алгеброй. Изучение алгебраических дробей является неотъемлемой частью обучения алгебре на всех уровнях школьной и университетской программы.
Понятие алгебраической дроби

Алгебраическая дробь может быть простой или составной. Простые алгебраические дроби содержат только один многочлен и не могут быть упрощены дальше. Составные же дроби представляют собой сумму или разность нескольких простых дробей.
Алгебраические дроби используются для решения уравнений, интегрирования функций и других задач математики.
Основные принципы упрощения алгебраической дроби

Упрощение алгебраической дроби включает в себя несколько основных принципов, которые помогают сделать выражение более компактным и удобным для работы:
| 1. | Факторизация числителя и знаменателя. |
| 2. | Отыскание общего знаменателя для сложения или вычитания дробей. |
| 3. | Упрощение выражения путем сокращения общих множителей числителя и знаменателя. |
| 4. | Проверка на возможность дальнейшего упрощения и сокращения дроби. |
Понимание этих принципов позволяет проводить упрощение алгебраических дробей эффективно и точно, что является важным навыком при работе с алгебраическими выражениями.
Определение простейшей алгебраической дроби

Алгебраическая дробь называется простейшей, если степень числителя меньше степени знаменателя и не сокрушена. То есть дробь имеет вид:
$$\frac{P(x)}{Q(x)}$$, где степень многочлена $$P(x)$$ меньше степени многочлена $$Q(x)$$.
Простейшая алгебраическая дробь может быть представлена в виде суммы простейших дробей по одному на каждый линейный или квадратный множитель знаменателя.
Примеры преобразования алгебраической дроби

- Дробь \( \frac{x^2 + 2x - 3}{x^2 - 1} \) можно разложить на сумму простых дробей: \[ \frac{x^2 + 2x - 3}{x^2 - 1} = \frac{A}{x + 1} + \frac{B}{x - 1} \]
- Далее находим числа A и B путем умножения обеих сторон уравнения на общий знаменатель, раскрываем скобки и приравниваем коэффициенты при одинаковых степенях x: \[ x^2 + 2x - 3 = A(x - 1) + B(x + 1) \]
- Решаем полученное уравнение и находим значения A и B. Затем подставляем их обратно в исходное выражение.
Таким образом, мы представили алгебраическую дробь в виде суммы простых дробей и можем продолжить преобразования для дальнейшего анализа и вычислений.
Упрощение алгебраических дробей с разными знаменателями

При упрощении алгебраических дробей с разными знаменателями следует следовать нескольким шагам:
- Находим общий знаменатель дробей.
- Приводим дроби к общему знаменателю путем умножения числителя и знаменателя на необходимые множители.
- Складываем или вычитаем числители, при этом знаменатель остается общим.
- Дробь приводится к наименьшему знаменателю, если это возможно.
Важно помнить, что при упрощении алгебраических дробей необходимо быть внимательным и аккуратным, чтобы не допустить ошибок в расчетах.
Решение уравнений с применением алгебраических дробей

Для решения уравнений с использованием алгебраических дробей следует разложить дробь на простейшие дроби. Для этого:
| 1. | Выражаем дробь в виде суммы простейших дробей. |
| 2. | Находим неизвестные коэффициенты через систему уравнений, полученных из равенства исходной дроби с суммой простейших дробей. |
| 3. | Подставляем найденные коэффициенты в исходную дробь и решаем получившееся уравнение. |
Методы использования алгебраических дробей в уравнениях
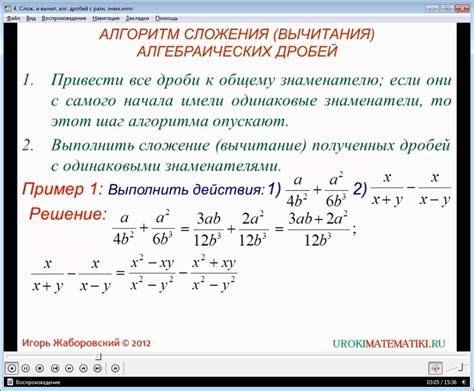
Алгебраические дроби встречаются в уравнениях при решении различных задач математического анализа. Существуют различные методы работы с алгебраическими дробями при их использовании в уравнениях.
1. Общий метод: При решении уравнений с алгебраическими дробями необходимо привести дроби к общему знаменателю и выполнить соответствующие действия с числителями. Этот метод является основным при решении большинства уравнений с дробями.
2. Метод разложения на простейшие дроби: Для решения сложных уравнений с алгебраическими дробями применяется метод разложения на простейшие дроби. Сначала дробь разлагается на сумму простейших дробей, а затем с помощью выражений, в которых фигурируют простейшие дроби, уравнение приводится к более простой форме.
3. Использование тождеств: При решении уравнений с алгебраическими дробями часто применяются различные математические тождества, такие как тождество Ньютона-Лейбница и другие, которые позволяют упростить выражения и облегчить дальнейшее решение.
Овладение указанными методами использования алгебраических дробей в уравнениях позволяет эффективно решать разнообразные задачи и получать точные математические результаты.
Деление алгебраических дробей

Для деления алгебраических дробей необходимо выполнить следующие шаги:
- Привести дроби к общему знаменателю.
- Разделить числители дробей.
- Разделить знаменатели дробей.
- Сократить полученную дробь при необходимости.
После проведения всех необходимых операций можно получить результат деления алгебраических дробей в виде упрощенной алгебраической дроби.
Вопрос-ответ

Что такое алгебраическая дробь?
Алгебраическая дробь представляет собой дробь, в которой как числитель, так и знаменатель содержат алгебраические выражения. Например, \( \frac{2x+1}{x^2-4} \) - это алгебраическая дробь.
Как упростить алгебраическую дробь?
Для упрощения алгебраической дроби нужно разложить числитель и знаменатель на множители, затем сократить общие множители и выполнить действия над получившимися выражениями. Например, для дроби \( \frac{2x^2+4x}{3x+6} \) можно разделить числитель и знаменатель на 2 и упростить до \( \frac{x^2+2x}{3} \).



