Когда мы говорим о векторах и их взаимодействии, одно из самых удивительных и важных понятий, которое стоит осветить, - это форма, которая определяет их взаимосвязь друг с другом. Это своеобразное "оружие" в мире математики, позволяющее нам определить направление и степень влияния одного вектора на другой.
Давайте представим, что каждый вектор - это отдельная сила, которая может воздействовать на другой вектор. Именно эта зависимость становится ключевой в понимании и анализе векторного пространства. Однако, чтобы полностью охватить эту идею, нам нужно ознакомиться с одним из сложнейших и фундаментальных понятий математики - билинейной формой.
Билинейная форма - это специальный тип математического объекта, который позволяет нам определить, насколько сильно и в каком направлении один вектор воздействует на другой. Она представляет собой мощное средство для анализа и изучения различных физических и геометрических явлений. Благодаря билинейной форме, мы можем понять, как векторы влияют друг на друга и как они способны изменяться с различными условиями.
Основные аспекты концепции билинейной формы в линейной алгебре

В рамках изучения линейной алгебры необходимо иметь понимание основных аспектов, связанных с билинейной формой. Рассмотрим важные аспекты этой концепции, которые помогут нам построить понимание о взаимосвязи между векторами и отображениями.
Линейные пространства: Для начала, для понимания билинейной формы необходимо разобраться в основных понятиях линейного пространства. Линейное пространство представляет собой абстрактную структуру, которая удовлетворяет определенным условиям, связанным с операциями сложения и умножения на скаляр. Оно позволяет работать с векторами и их комбинациями.
Билинейные отображения: Одним из важных аспектов билинейной формы является билинейное отображение. Билинейное отображение задает связь между двумя линейными пространствами, исследуя их взаимодействие и сопоставляя элементы обоих пространств.
Базисы и координаты: Для работы с билинейной формой нам необходимо понимание базисов и координат в линейном пространстве. Базис – это конечный набор линейно независимых векторов, который порождает все остальные вектора пространства. Координаты же позволяют нам представить вектор в виде упорядоченной совокупности чисел.
Симметричность и кососимметричность: Билинейная форма может быть как симметричной, так и кососимметричной. Симметричность означает, что значение билинейной формы для двух векторов не зависит от порядка этих векторов. Кососимметричность же подразумевает, что значение билинейной формы меняет знак при перестановке векторов.
Изучение этих основных аспектов позволит создать базовое понимание о билинейных формах и их значении в линейной алгебре. Это открывает двери для более глубокого исследования данной темы и ее применения в различных областях математики и физики.
Связь между билинейной формой и операцией скалярного умножения векторов

В данном разделе рассмотрим связь между двумя важными математическими понятиями: билинейной формой и операцией скалярного умножения векторов. Несмотря на то, что данные понятия звучат разными словами, они на самом деле тесно связаны и имеют далеко идущие параллели.
Билинейная форма является алгебраическим объектом, позволяющим осуществлять определенные операции над векторами. Она является функцией, принимающей на вход два вектора и возвращающей скалярное значение. Скалярное же произведение векторов - это умножение координат двух векторов с последующим сложением полученных произведений, что также приводит к получению скалярного значения. Таким образом, можно утверждать, что билинейная форма и операция скалярного умножения векторов имеют схожую природу и выполняют аналогичные действия над векторами.
Одна из ключевых разниц между билинейной формой и операцией скалярного умножения состоит в области их применения. Билинейная форма используется для решения различных задач линейной алгебры, таких как нахождение базиса, проверка ортогональности векторов и решение систем линейных уравнений. Скалярное же произведение векторов широко применяется в геометрии для нахождения длины вектора, определения угла между векторами и решения других задач, связанных с пространственными координатами.
Для наглядности приведена таблица, иллюстрирующая основные схожести и различия между билинейной формой и скалярным произведением векторов:
| Билинейная форма | Скалярное произведение векторов |
|---|---|
| Принимает на вход два вектора и возвращает скалярное значение | Умножает координаты двух векторов и возвращает скалярное значение |
| Используется в линейной алгебре для решения задач | Используется в геометрии для нахождения длины вектора и угла между векторами |
Пример применения билинейной формы в геометрии
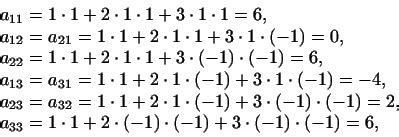
Для иллюстрации этой идеи рассмотрим пример смазанной поверхности. Смазанная поверхность – это абстрактный объект, который служит для описания визуальных эффектов плавности и покрытия различных объектов в геометрии. Она задается парой векторов, которые определяют две главные оси смазанной поверхности.
| Ось X | Ось Y | Описание |
|---|---|---|
| Вперед | Вправо | Плавно перетекает цвет от темного к светлому |
| Влево | Вниз | Создает эффект рельефности и текстуры |
| Вверх | Назад | Имитирует эффект зеркального отражения |
Таким образом, применение билинейной формы в геометрии позволяет создавать уникальные и захватывающие визуальные эффекты, которые отражают естественные процессы и свойства окружающего мира. Это является одним из множества примеров использования билинейной формы в различных областях науки и техники.
Симметричность и антисимметричность билинейной формы
В данном разделе мы рассмотрим важные свойства билинейной формы, которые называются симметричностью и антисимметричностью. Эти свойства позволяют нам более глубоко понять и интерпретировать взаимодействие двух векторов.
Симметричность билинейной формы подразумевает, что значения формы не зависят от порядка векторов. То есть, если мы поменяем местами векторы, значение билинейной формы останется неизменным. Наличие симметричности позволяет нам говорить о взаимном воздействии векторов, которое не зависит от их положения относительно друг друга.
С другой стороны, антисимметричность билинейной формы предполагает, что значения формы изменяются сменой местами векторов и получают противоположные знаки. Это означает, что билинейная форма учитывает ориентацию и направление векторов в пространстве. Антисимметричность позволяет нам выявлять и анализировать различные аспекты взаимодействия векторов, такие как их направления, скорость изменения и т.д.
- Симметричность билинейной формы:
- Значения не зависят от порядка векторов
- Интерпретация взаимодействия
- Антисимметричность билинейной формы:
- Значения изменяются сменой местами векторов
- Учет ориентации и направления векторов
- Выявление различных аспектов взаимодействия
Вычисление значения операции, комбинирующей два векторных объекта
В данном разделе рассмотрим методы вычисления значения операции, которая сочетает два векторных объекта, подобно взаимодействию двух физических сущностей, обладающих определенными характеристиками.
Прежде чем приступить к вычислению, необходимо определиться с типом операции, которую мы хотим выполнить. Существуют различные способы сочетания векторных объектов, каждый из которых может подчеркивать определенные свойства или характеристики в процессе вычисления.
Один из методов вычисления значения операции - это использование математических формул, которые описывают соответствующее взаимодействие между векторными объектами. Эти формулы основаны на принципах линейной алгебры и могут варьироваться в зависимости от конкретных задач и целей.
Другой способ вычисления состоит в использовании таблицы или матрицы, где каждая ячейка представляет собой значение операции для конкретных комбинаций векторных объектов. Это позволяет наглядно отобразить результаты операции и обеспечивает удобство при их поиске и анализе.
Также можно применять и другие методы вычисления значений операции, например, с использованием геометрических моделей или специализированных программных пакетов. Важно выбрать подходящий метод, учитывая особенности векторных объектов и требования конкретной задачи.
- Методы вычисления формул
- Таблица или матрица значений операции
- Геометрические модели и программные пакеты
Матричное представление билинейной формы
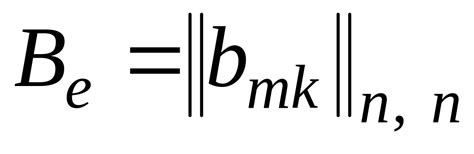
В данном разделе рассмотрим способы представления билинейной формы при помощи матрицы. Такое представление позволяет упростить вычисления и анализ свойств формы, а также наглядно отобразить ее структуру.
Матричное представление билинейной формы основывается на идее о том, что каждая билинейная форма может быть задана с помощью матрицы. Конкретные элементы матрицы определяются значениями билинейной формы для соответствующих пар векторов.
Для начала, рассмотрим случай билинейной формы на двумерном пространстве. В этом случае матрица будет иметь размерность 2x2, и каждый элемент матрицы будет соответствовать произведению соответствующих компонент двух векторов исходной формы.
Для общего случая билинейной формы в n-мерном пространстве, матрица будет иметь размерность nxn. В этом случае каждый элемент матрицы будет представлять собой произведение соответствующих компонент векторов, умноженное на коэффициент билинейной формы.
Матричное представление билинейной формы позволяет удобно работать с операциями над векторами и анализировать свойства формы на основе ее матричного представления. Оно также облегчает решение систем линейных уравнений, связанных с билинейной формой, и позволяет проводить компьютерные вычисления с использованием матричных операций.
Критерии невырожденности билинейной формы
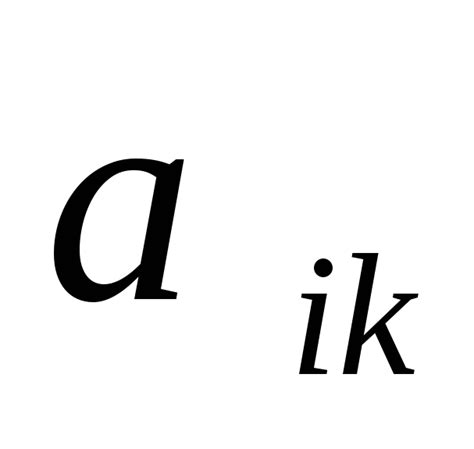
В данном разделе рассмотрим критерии, позволяющие определить невырожденность билинейной формы. Невырожденность представляет собой важное свойство, обеспечивающее ее полезность в различных областях науки и инженерии.
Первый критерий, который мы рассмотрим, основывается на идеи линейной независимости векторов, на которых действует билинейная форма. Если при заданной билинейной форме значения равны нулю только при значениях векторов, равных нулю, то такая форма называется невырожденной. Это означает, что существуют ненулевые векторы, на которых билинейная форма принимает ненулевое значение.
Второй критерий, связанный с невырожденностью, основывается на понятии обратной матрицы. Если матрица билинейной формы невырождена, то она имеет обратную матрицу, что позволяет нам осуществлять обратное преобразование при решении систем уравнений. Таким образом, наличие обратной матрицы является полезным свойством, которое упрощает анализ и решение различных задач, связанных с билинейными формами.
Третий критерий, который мы рассмотрим, связан с определителем матрицы билинейной формы. Если определитель равен нулю, то форма является вырожденной. В этом случае билинейная форма не способна различать разные векторы и несет меньше информации. Если определитель не равен нулю, то форма невырожденная.
Итак, мы рассмотрели три основных критерия невырожденности билинейной формы: линейная независимость векторов, наличие обратной матрицы и определитель, не равный нулю. Невырожденная билинейная форма позволяет эффективно работать с векторами, обладает обратимостью и предоставляет больше информации при анализе различных задач.
Применение билинейной формы в физике

Взаимодействие двух физических объектов или систем можно рассматривать через применение билинейной формы, которая позволяет описать их отношения с помощью математических операций, не привязываясь к их конкретным свойствам. Этот метод может быть полезен, когда точное определение и измерение физической величины затруднено или несостоятельно.
Билинейная форма позволяет проводить анализ взаимодействия между различными физическими объектами, такими как электрические заряды, магнитные поля или механические системы. С её помощью можно описать и предсказывать изменение энергии, потока или силы, возникающих между этими объектами в зависимости от их характеристик и взаимного расположения.
Применение билинейной формы в физике имеет широкий спектр применений, включая расчет электрического и магнитного поля, анализ динамики и колебаний объектов, определение траекторий и скоростей движения, а также моделирование сложных физических систем. Этот подход помогает исследователям и инженерам детально понять и предсказать поведение физических систем на основе их внутренних характеристик и взаимодействий.
Сопоставление билинейной формы с альтернативными подходами

В данном разделе мы рассмотрим возможные формы, которые могут сопоставляться с билинейной формой и проведем сравнительный анализ их особенностей. Рассмотрение альтернативных форм поможет нам более полно понять и оценить роль и значение билинейной формы в решении различных математических и прикладных задач.
Наиболее распространенной альтернативой билинейной формы является другой вид формы, имеющей свою уникальную природу и свойства. Эта форма, по аналогии с билинейной, способна описывать зависимости и взаимодействия между математическими объектами, но использует иную систему измерений и параметров. В свою очередь, применение данной альтернативной формы может быть оправдано в конкретных сферах науки и техники, где требуется точность измерения, представление данных или моделирование сложных систем.
Важным аспектом при сравнении билинейной формы с альтернативными формами является понимание сходств и различий между ними. Возможно, изначально конкретная форма может показаться более удобной и применимой в контексте данной проблемы, но глубокий анализ и сравнение с другими формами могут раскрыть новые аспекты и перспективы исследования.
Проведение сравнительного анализа требует участия различных дисциплин и экспертов, так как каждая форма имеет свои особенности и применяется в разных предметных областях. В итоге, сравнение билинейной формы с другими формами позволит нам более глубоко понять ее преимущества, недостатки и потенциалы для развития в будущем.
Вопрос-ответ

Что такое билинейная форма?
Билинейная форма - это функция, принимающая два вектора и возвращающая скалярное значение. Она обладает линейностью по каждому из аргументов.
Какова роль билинейной формы в математике?
Билинейная форма играет важную роль во многих областях математики, включая линейную алгебру и анализ. Она помогает определить скалярное произведение двух векторов и решать различные задачи, связанные с векторными пространствами.
В чем отличие билинейной формы от линейной формы?
В отличие от билинейной формы, линейная форма принимает только один вектор и возвращает скаляр. Она линейна только по этому вектору, в то время как билинейная форма линейна по каждому из своих аргументов.
Как связана билинейная форма с скалярным произведением?
Билинейная форма позволяет вычислить скалярное произведение двух векторов векторного пространства. Для этого необходимо задать определенную билинейную форму, которая будет удовлетворять определенным свойствам и правилам. С помощью билинейной формы можно определить угол между векторами, вычислить их проекции и решать другие задачи, связанные с скалярным произведением.



