Единица в степени мнимой единицы – одно из удивительных математических понятий, порожденное алгеброй и комплексными числами. Это выражение часто вызывает недоумение и интерес у тех, кто сталкивается с ним впервые. Разгадывая его смысл, мы заглянем в мир комплексных чисел, где реальность переплетается с мнимым.
Мнимая единица i, также известная как мнимая единица, является ключевым элементом в теории комплексных чисел. Одной из интереснейших свойств этой мнимой единицы является возведение в степень i, где удивительным образом возникает число, которое кажется невероятным для тех, кто привык к обычным действительным числам.
Благодаря своей особенной природе и нестандартному поведению, число единицы в степени мнимой единицы становится объектом исследований математиков и является одним из удивительных феноменов, демонстрирующих богатство и разнообразие математического мира.
Расшифровка значения единицы

Тогда единица в степени мнимой единицы выражается как ii, где ii = ei(ln|i|π/2).
Значение ii может быть расшифровано как e в степени (-π/2), что примерно равно 0.20788.
Таким образом, значение единицы i в степени самой себя оказывается весьма удивительным и неочевидным, что делает эту математическую константу интересной для изучения.
Какую роль играет единица в степени мнимой?

Единица в степени мнимой входит в комплексное число и обозначается как i. Это важная математическая концепция, которая позволяет работать с мнимыми числами и решать задачи, где встречаются квадратные корни из отрицательных чисел.
Важные свойства единицы в степени мнимой:
1. Квадрат единицы i равен -1: i^2 = -1.
2. При возведении в степень i последовательно появляются значения: i^1 = i, i^2 = -1, i^3 = -i, i^4 = 1.
Использование единицы в степени мнимой позволяет упростить вычисления и представить решения в более удобной форме.
Свойства единицы в степени мнимой
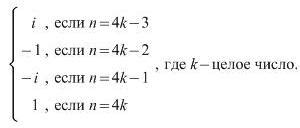
1. Умножение на мнимую единицу: Если действительная часть комплексного числа равна нулю, то умножение на мнимую единицу приводит к появлению комплексного числа вида bi. Это позволяет работать с комплексными числами как с обычными векторами, что упрощает решение многих математических задач.
2. Повторные степени мнимой единицы: Важное свойство мнимой единицы заключается в том, что i в четвертой степени равно единице: i^4 = 1. Это свойство особенно полезно при вычислении корней комплексных чисел.
Какие особенности проявляет единица в комплексных числах?

| Умножение | Умножение на i приводит к повороту на 90 градусов против часовой стрелки в комплексной плоскости. |
| Возведение в степень | i возводится в квадрат даёт -1, i в кубе даёт -i, i в четвёртой степени даёт 1. Таким образом, i^2 = -1. |
| Поведение в степени | Степень i повторяет циклически четыре значения: i, -1, -i, 1. |
Функциональное значение единицы
Единица в степени мнимой единицы применяется в различных областях математики и физики, таких как комплексный анализ и электротехника.
В комплексном анализе единица в степени мнимой единицы играет важную роль при решении уравнений и интегралов, позволяя ученным и инженерам справляться с задачами, которые требуют работы с комплексными числами.
В электротехнике использование единицы в степени мнимой единицы помогает учитывать фазовые сдвиги и взаимодействие между активной и реактивной энергией в электрических цепях.
Вопрос-ответ

Что такое единица в степени мнимой единицы?
Единица в степени мнимой единицы — это математическое выражение, обозначаемое как i^i, где i — мнимая единица. Расшифровывается как i умножить на i.
Какое значение имеет i в математике?
Мнимая единица i в математике обладает свойством, что i^2 = -1. Это позволяет выполнять вычисления при работе с комплексными числами и решать уравнения, которые иначе были бы неразрешимыми.
Как вычислить i в степени i?
Чтобы вычислить i в степени i, нужно воспользоваться формулой Эйлера: i^i = exp(-π/2). Это приблизительно равно 0.2079.
Какие свойства имеет единица в степени мнимой единицы?
Единица в степени мнимой единицы обладает интересными свойствами, такими как возникновение вещественного числа при возведении в эту степень. Также значение i^i зависит от значения логарифма комплексного числа.
В каких областях математики используется единица в степени мнимой единицы?
Единица в степени мнимой единицы находит применение в различных математических рассуждениях, в теории чисел, теории вероятностей, теории функций и других областях. Она также используется в физике и других науках.



