В математике существует понятие взаимно простых чисел, которые не имеют общих делителей, кроме единицы. Для того чтобы узнать, являются ли числа 24 и 35 взаимно простыми, необходимо выяснить их общие делители.
Число 24 разлагается на простые множители как 2^3 * 3, а число 35 - как 5 * 7. Очевидно, что 24 и 35 имеют общих делителей: 1 и 5. Таким образом, числа 24 и 35 не являются взаимно простыми.
Числа 24 и 35: взаимная простота

Число 24 разлагается на простые множители как 2^3 * 3. А число 35 разлагается на 5 * 7.
Общих делителей у чисел 24 и 35 нет, поэтому они являются взаимно простыми.
Определение взаимной простоты чисел

Проверка на взаимную простоту

Основные свойства взаимно простых чисел
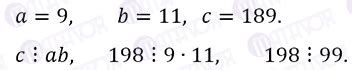
Основные свойства взаимно простых чисел:
- Взаимно простые числа всегда имеют только один общий делитель - число 1.
- Если два числа взаимно просты, их произведение также будет взаимно простым с числом один.
- Если число а взаимно просто с числом b, то обратное утверждение верно - число b взаимно просто с числом a.
- Взаимно простые числа широко используются в теории чисел, криптографии и других областях математики.
Общие делители чисел 24 и 35
Числа 24 и 35: наибольший общий делитель

Для определения наибольшего общего делителя чисел 24 и 35 можно воспользоваться алгоритмом Евклида. Этот метод предполагает последовательное нахождение остатка от деления двух чисел, пока одно из них не станет равным нулю. На каждом шаге делим большее число на меньшее и заменяем большее число остатком. Последний ненулевой остаток и будет наибольшим общим делителем исходных чисел.
Для чисел 24 и 35:
- 24 / 35 = 0 (остаток 24)
- 35 / 24 = 1 (остаток 11)
- 24 / 11 = 2 (остаток 2)
- 11 / 2 = 5 (остаток 1)
- 2 / 1 = 2 (остаток 0)
Таким образом, наибольший общий делитель чисел 24 и 35 равен 1. Поскольку он равен 1, числа 24 и 35 являются взаимно простыми.
Числа 24 и 35: соотношение взаимной простоты

Число 24 можно разложить на простые множители: 24 = 2^3 * 3. Число 35 разложим на простые множители: 35 = 5 * 7.
Из разложения видно, что общих простых множителей у чисел 24 и 35 нет, так как числа не имеют общих делителей, кроме 1. Следовательно, числа 24 и 35 являются взаимно простыми.
Проверка на взаимную простоту методом Евклида

Шаги метода Евклида:
- Найдем наибольший общий делитель (НОД) чисел 24 и 35. Для этого применим следующие шаги:
- Разделим большее число на меньшее: 35 ÷ 24 = 1 (остаток 11).
- Теперь разделим предыдущее меньшее число (24) на полученный остаток (11): 24 ÷ 11 = 2 (остаток 2).
- Повторим этот процесс, пока не получим остаток 0.
Таким образом, метод Евклида подтверждает, что числа 24 и 35 являются взаимно простыми.
Вопрос-ответ

Являются ли числа 24 и 35 взаимно простыми?
Нет, числа 24 и 35 не являются взаимно простыми, так как они имеют общие делители, такие как 1, 2 и 4. Взаимно простые числа не имеют общих делителей, кроме 1.
Почему числа 24 и 35 не взаимно просты?
Числа 24 и 35 имеют общие делители, такие как 1, 2 и 4. Для того чтобы числа были взаимно простыми, они должны быть такими, что у них нет общих делителей, кроме 1. В данном случае, оба числа имеют общие делители, поэтому они не являются взаимно простыми.
Как определить, являются ли числа 24 и 35 взаимно простыми?
Для того чтобы определить, являются ли числа взаимно простыми, нужно найти их общие делители. Если числа имеют только один общий делитель - 1, то они взаимно просты. В случае с числами 24 и 35, у них есть общие делители 1, 2 и 4, следовательно, они не являются взаимно простыми.
Какие делители имеют числа 24 и 35?
Число 24 имеет делители 1, 2, 3, 4, 6, 8, 12 и 24. Число 35 имеет делители 1, 5, 7 и 35. Оба числа имеют общие делители 1, 2, 4, следовательно, они не являются взаимно простыми.
Могут ли числа 24 и 35 быть взаимно простыми?
Нет, числа 24 и 35 не могут быть взаимно простыми, так как имеют общие делители. Для того чтобы числа были взаимно простыми, у них должен быть только один общий делитель - 1. В данном случае, у 24 и 35 есть общие делители 1, 2 и 4, поэтому они не могут быть взаимно простыми.



