Дискриминант квадратного уравнения - это выражение, которое позволяет определить, сколько корней у этого уравнения. Если дискриминант равен нулю, то у уравнения будет один корень.
Для того чтобы определить, что дискриминант равен нулю, нужно найти выражение под знаком радикала в формуле дискриминанта и вычислить его значение. Если результат равен нулю, то дискриминант равен нулю.
Найдем корень квадратного уравнения с дискриминантом равным нулю. Для этого нам необходимо воспользоваться формулой x = -b/(2a), где a, b, c - коэффициенты квадратного уравнения ax^2 + bx + c = 0.
Определение понятия дискриминант в математике

Формула вычисления дискриминанта в квадратном уравнении

Для квадратного уравнения вида ax^2 + bx + c = 0 дискриминант можно вычислить по формуле:
Дискриминант:
D = b^2 - 4ac
Если дискриминант равен нулю (D = 0), то у уравнения есть один корень. Если дискриминант положителен (D > 0), то у уравнения два различных корня. В случае отрицательного дискриминанта (D
Как правильно использовать дискриминант для определения корней квадратного уравнения
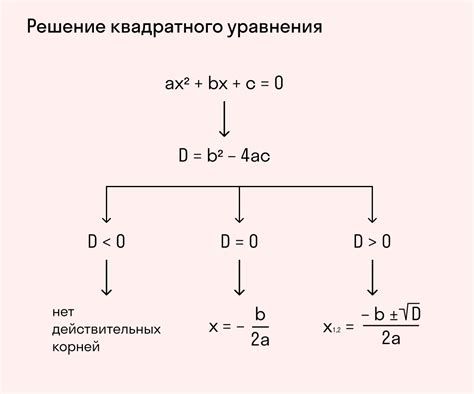
Если дискриминант равен нулю (D = 0), то у уравнения есть один действительный корень, который можно найти по формуле x = -b/2a.
Если дискриминант больше нуля (D > 0), то у уравнения два действительных корня, которые можно найти по формулам x1 = (-b + √D) / 2a и x2 = (-b - √D) / 2a.
Если дискриминант меньше нуля (D
Описание условия, при котором дискриминант равен нулю

Дискриминант квадратного уравнения равен нулю тогда и только тогда, когда уравнение имеет ровно один корень.
Это происходит в случае, когда график квадратного уравнения касается оси абсцисс, т.е. имеет одну точку пересечения с этой осью.
Шаги по вычислению корня квадратного уравнения при нулевом дискриминанте

Для определения корня квадратного уравнения при нулевом дискриминанте следует выполнить следующие шаги:
- Разложить уравнение вида ax^2 + bx + c = 0 по формуле дискриминанта: D = b^2 - 4ac.
- Подставить известные значения коэффициентов a, b и c в формулу дискриминанта и вычислить его значение.
- Если дискриминант D равен нулю, то квадратное уравнение имеет один вещественный корень, который можно найти по формуле: x = -b/(2a).
- Подставить значения коэффициентов a и b в формулу для нахождения корня и выполнить вычисления.
После этих шагов можно определить и найти корень уравнения при нулевом значении дискриминанта.
Примеры решения уравнений с нулевым дискриминантом
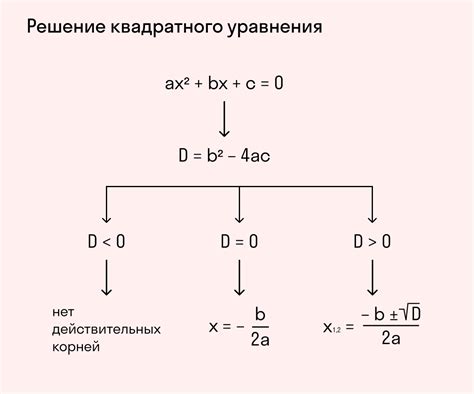
Дискриминант D = (-4)^2 - 4*1*4 = 0
Так как D равен нулю, уравнение имеет один корень.
Решение: x = -(-4) / 2*1 = 2
2. Уравнение: 3x^2 - 6x + 3 = 0
Дискриминант D = (-6)^2 - 4*3*3 = 0
Так как D равен нулю, уравнение имеет один корень.
Решение: x = -(-6) / 2*3 = 1
Интерпретация результатов и нахождение корней

Если дискриминант квадратного уравнения равен нулю, то это означает, что уравнение имеет ровно один корень. Этот корень можно найти, используя формулу:
x = -b/2a
где a, b и c - коэффициенты квадратного уравнения ax^2 + bx + c = 0. Подставив значения a, b и c, можно найти значение корня x. Этот корень будет являться уникальным решением уравнения при нулевом дискриминанте.
Сравнение случаев с нулевым и отличным от нуля дискриминантом
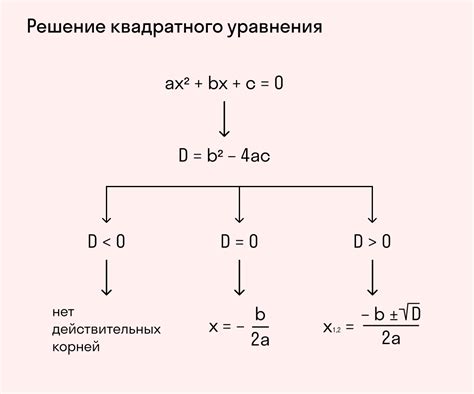
Для квадратного уравнения с дискриминантом равным нулю, у нас есть только один корень. Этот корень будет совпадать. При этом график уравнения будет касаться оси ОХ, образуя единственную точку касания.
Если же дискриминант отличен от нуля, то имеется два различных корня уравнения. Геометрически это соответствует пересечению графика функции с осью ОХ в двух точках.
Практическое применение полученных знаний в математике

Практическое применение полученных знаний в математике также проявляется в решении задач из различных областей, например, в физике при моделировании движения тела, в экономике при анализе рыночных тенденций, а также в других научных и инженерных дисциплинах.
Использование знаний о дискриминанте и его связи с корнями квадратного уравнения поможет вам не только в школьном курсе математики, но и в решении реальных задач, где математические методы играют важную роль.
Значение и применение на практике новых навыков вычисления корней квадратного уравнения
Определение корней квадратного уравнения на практике имеет широкое применение в различных областях, таких как физика, экономика, информатика. Например, в физике задачи находятся решения уравнений для определения траектории движения тела, время полета объекта и т.д. В экономике корни уравнений могут использоваться для прогнозирования, анализа рыночной динамики и определения оптимальных решений.
| Применение | Область |
| Определение корней уравнения | Математика |
| Анализ функций | Физика |
| Прогнозирование и оптимизация | Экономика |
Вопрос-ответ

Как определить, что дискриминант равен нулю?
Дискриминант равен нулю в квадратном уравнении, когда уравнение имеет один корень. Дискриминант определяется по формуле D = b^2 - 4ac, где a, b, c - коэффициенты квадратного уравнения ax^2 + bx + c = 0. Если D = 0, то уравнение имеет один корень.
Как найти корень квадратного уравнения, если дискриминант равен нулю?
Если дискриминант квадратного уравнения равен нулю, то уравнение имеет один корень. Для нахождения этого корня используется формула x = -b / 2a, где a, b - коэффициенты перед x в уравнении ax^2 + bx + c = 0. Подставив значение b и a, найденное из уравнения, вы получите корень уравнения.
Что означает, если дискриминант равен нулю?
Если дискриминант квадратного уравнения равен нулю, это означает, что уравнение имеет ровно один корень. Этот случай называется кратным корнем, и он возникает, когда вершина параболы лежит на оси абсцисс. Дискриминант равный нулю является специальным случаем, который требует особого внимания при решении уравнения.
Какой геометрический смысл имеет ситуация, когда дискриминант квадратного уравнения равен нулю?
Когда дискриминант квадратного уравнения равен нулю, это означает, что уравнение имеет один корень, и парабола, заданная уравнением, касается оси абсцисс. Геометрически это соответствует ситуации, когда парабола с вершиной на оси абсцисс касается этой оси, что является специфическим случаем в геометрии параболы.



