Тригонометрические функции синус, косинус, тангенс и котангенс широко применяются в математике и естественных науках. Но что делать, если нам нужно вычислить угол, при котором значение той или иной тригонометрической функции равно известному числу? Для этого существуют обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс.
Арксинус и арккосинус определяются как обратные функции к синусу и косинусу соответственно. То есть, если у нас есть число от -1 до 1, мы можем найти угол, удовлетворяющий условию синуса или косинуса равному этому числу.
Арктангенс и арккотангенс относятся к обратным функциям тангенса и котангенса. Они помогают нам найти угол, при котором значение тангенса или котангенса соответствует заданному числу.
Дифференцированные функции
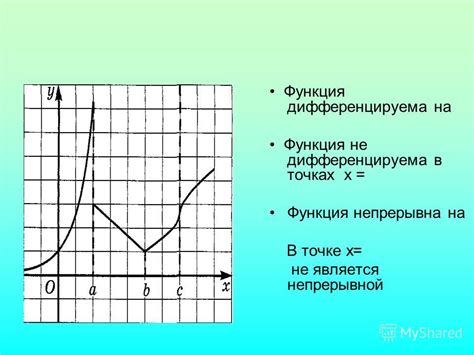
Дифференцирование функции происходит путем нахождения производной функции. Производная функции в данной точке равна скорости изменения функции в этой точке.
Дифференцированные функции используются в математическом анализе для изучения поведения функций и построения графиков функций.
Арксинус: суть и особенности

| Особенности арксинуса: |
| 1. Область значений арксинуса ограничена на отрезке от -π/2 до π/2. |
| 2. Арксинус является нечетной функцией. |
| 3. Значение арксинуса определено для всех действительных чисел в интервале [-1, 1]. |
| 4. Значение арксинуса выражается в радианах. |
Арккосинус: определение и применение

Арккосинус принимает значения из интервала от 0 до π и осуществляет обратное преобразование угла косинуса в сам угол. То есть, если cos(x) = y, то arccos(y) = x.
Применение арккосинуса в математике широко распространено, так как он помогает находить углы по заданным значениям косинуса, что полезно при решении геометрических задач и тригонометрических уравнений.
Арктангенс: основные свойства и значения

Основное свойство арктангенса: arctan(tg(α)) = α, для α из (-π/2, π/2).
Значения арктангенса принимаются в радианах, и их область значения лежит в интервале (-π/2, π/2).
Арккотангенс: преимущества и примеры использования

Преимущества арккотангенса:
Арккотангенс (арккотгенс) имеет широкое применение в уравнениях и задачах, связанных с тригонометрией. С его помощью можно находить углы, выраженные через катет и гипотенузу правильного прямоугольного треугольника, что упрощает решение сложных задач и уравнений.
Примеры использования арккотангенса:
1. Нахождение углов в прямоугольном треугольнике по значениям катетов и гипотенузы.
2. Решение уравнений и задач, связанных с углами и сторонами треугольника.
3. Применение в физике, геометрии и других науках для определения углов и длин сторон треугольников.
Вопрос-ответ

Что такое арксинус?
Арксинус - это обратная функция к синусу. Она обозначается как arcsin или sin^(-1). Арксинус возвращает угол, значение синуса которого равно заданному числу. Например, arcsin(0.5) = 30°, так как sin(30°) = 0.5.
Как определить аргументы арккосинуса?
Арккосинус - это обратная функция к косинусу. Она обозначается как arccos или cos^(-1). Аргументы арккосинуса должны быть в диапазоне от -1 до 1, так как косинус принимает значения в этом интервале. Например, arccos(0) = 90°, arccos(1) = 0°, arccos(-1) = 180°.
Как связаны арктангенс и тангенс?
Арктангенс - это обратная функция к тангенсу. Она обозначается как arctan или tan^(-1). Арктангенс возвращает угол, значение тангенса которого равно заданному числу. Например, arctan(1) = 45°, так как tan(45°) = 1.
Чем отличаются арктангенс и арккотангенс?
Арктангенс и арккотангенс являются обратными функциями к тангенсу и котангенсу соответственно. Арктангенс обозначается как arctan или tan^(-1), а арккотангенс как arccot или cot^(-1). Основное отличие между ними заключается в том, что арктангенс возвращает угол, а арккотангенс возвращает аргумент. Например, arctan(1) = 45°, а arccot(1) = arccot(1/1) = 45°.



