Вы, вероятно, знакомы с понятием периметра – это сумма длин всех сторон многоугольника. Также вы знаете, что высота – это отрезок, опущенный из вершины многоугольника на противоположную сторону. Но что если мы хотим найти произведение периметра и высоты?
Для этого нам понадобится специальная формула, которая позволяет нам вычислить данное произведение. Это очень полезное знание, которое может пригодиться при решении различных задач по геометрии. Давайте рассмотрим эту формулу более подробно, чтобы понять, как она работает.
Формула для нахождения произведения периметра и высоты: произведение периметра и высоты равно площади многоугольника. Это значит, что если мы умножим периметр фигуры на ее высоту, мы получим площадь этой фигуры. Это свойство можно легко доказать, используя базовые знания о геометрии и алгебре.
Формула периметра и высоты
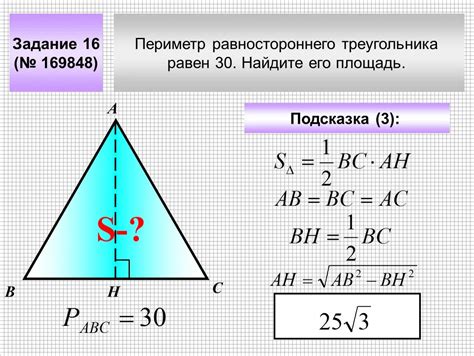
Для нахождения произведения периметра и высоты треугольника можно воспользоваться следующей формулой:
Произведение периметра и высоты треугольника равно удвоенной площади треугольника.
Или математически это можно записать так:
2 * P * h = S,
где P - периметр треугольника, h - высота треугольника, S - площадь треугольника.
Формула нахождения периметра

- Для прямоугольника: P = 2*(a + b), где a и b - длины сторон.
- Для квадрата: P = 4a, где a - длина стороны.
- Для треугольника: P = a + b + c, где a, b, c - длины сторон.
- Для круга: P = 2πr, где r - радиус круга.
Зная формулу для нахождения периметра, можно быстро и легко определить длину всех сторон фигуры и вычислить их сумму.
Формула вычисления высоты треугольника
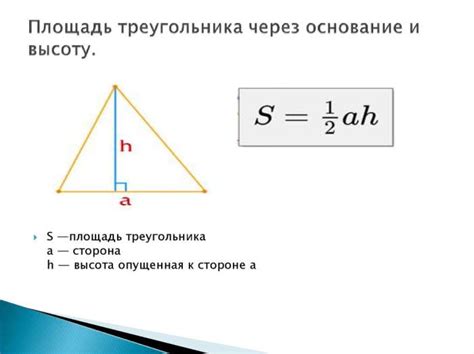
- Для равнобедренного треугольника: высота равна катету, опущенному из вершины треугольника.
- Для прямоугольного треугольника: высота, проведенная к гипотенузе, равна произведению катетов, деленному на гипотенузу.
- Для произвольного треугольника: высота может быть найдена по формуле геометрического места точек, равноудаленных от сторон треугольника.
Зная стороны треугольника, можно применить соответствующую формулу для вычисления высоты и далее использовать ее в различных задачах решения треугольников.
Связь периметра и высоты
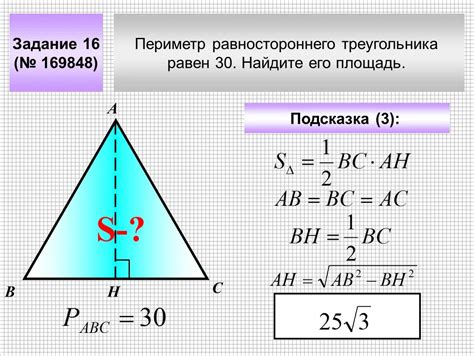
Для прямоугольного треугольника формула имеет вид: произведение периметра и высоты равно удвоенной площади треугольника. Это позволяет нам легко вычислить одну величину, зная другую. Для других многоугольников формулы выражают более сложные математические зависимости между периметром и высотой.
Примеры применения формулы
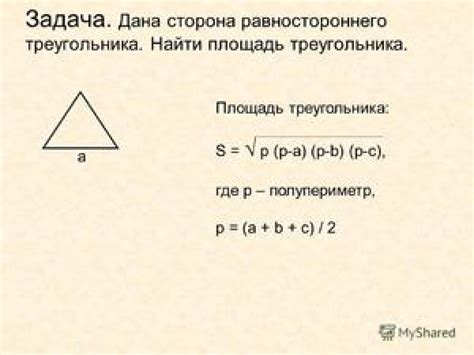
Пример 1: Рассмотрим прямоугольник со сторонами a = 5 см и b = 3 см. Его периметр равен P = 2a + 2b = 2 * 5 + 2 * 3 = 10 + 6 = 16 см. Пусть высота равна h = 4 см. Тогда произведение периметра и высоты равно Ph = 16 * 4 = 64 см.
Пример 2: Пусть у нас есть треугольник со сторонами a = 8 см, b = 10 см, c = 6 см. Его периметр равен P = a + b + c = 8 + 10 + 6 = 24 см. Пусть высота равна h = 5 см. Тогда произведение периметра и высоты равно Ph = 24 * 5 = 120 см.
| Пример | Периметр (P), см | Высота (h), см | Произведение Ph, см |
|---|---|---|---|
| Пример 1 | 16 | 4 | 64 |
| Пример 2 | 24 | 5 | 120 |
Вопрос-ответ

Как найти произведение периметра и высоты?
Для того чтобы найти произведение периметра и высоты, необходимо знать формулу, которая выражает это соотношение. Формула для нахождения произведения периметра и высоты прямоугольника представляется как P*h = 2*(a+b)*h, где P - периметр, h - высота, а и b - стороны прямоугольника. Данная формула позволяет найти произведение периметра и высоты при известных значениях периметра, высоты и сторон прямоугольника.
Какой смысл имеет произведение периметра и высоты в математике?
Произведение периметра и высоты в математике играет важную роль при решении задач, связанных с прямоугольниками. Это значение позволяет более полно охарактеризовать геометрическую фигуру и найти связь между периметром и высотой. Например, при решении задач на нахождение площади прямоугольника или определение его параметров, произведение периметра и высоты может быть полезным инструментом для расчетов.
Можно ли применить формулу для нахождения произведения периметра и высоты к другим фигурам?
Формула для нахождения произведения периметра и высоты, обычно используемая для прямоугольников, не всегда может быть применена к другим геометрическим фигурам. Для различных фигур существуют разные специфические формулы, которые учитывают их характеристики. Поэтому для каждой конкретной фигуры необходимо использовать соответствующие формулы для нахождения соотношений между периметром и высотой.



