Дифференциалы являются ключевым понятием в дифференциальном исчислении, а понимание их свойств и операций с ними необходимо для изучения математики и физики. В частности, возникает вопрос: что происходит при умножении дифференциала функции на дифференциал другой функции?
Ответ на этот вопрос зависит от специальных правил и свойств дифференциалов. Основное правило умножения дифференциалов утверждает, что произведение дифференциала одной функции на дифференциал другой функции равно добному оператору дифференцирования от произведения этих функций.
Разложение
Произведение дифференциала на дифференциал нельзя просто взять и умножить, как числа. Однако при разложении данного произведения можно учитывать свойства дифференциалов и правила дифференцирования.
Для разложения произведения дифференциала на дифференциал можно использовать различные методы, например, правила дифференцирования сложной функции или формулу произведения дифференциалов.
Важно помнить, что при разложении произведения дифференциалов необходимо учитывать взаимосвязь между переменными и выражениями, чтобы правильно провести дифференцирование и получить корректный результат.
Произведение двух дифференциалов

Дифференциал представляет собой бесконечно малое приращение функции. Произведение двух дифференциалов определяется как произведение двух бесконечно малых приращений:
| (dx) * (dy) = d(x * y) |
То есть произведение двух дифференциалов равно дифференциалу произведения соответствующих функций.
Математическая формула
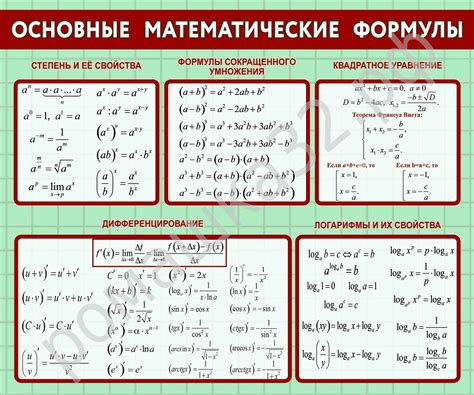
dx * dy = 0
Решение через дифференциальный оператор

Пусть имеется функция \( f(x) \), дифференцируемая на интервале \([a, b]\). Тогда произведение дифференциала функции \( f(x) \) на дифференциал переменной \( dx \) можно представить в виде:
\( df \cdot dx = (d_xf) \cdot dx \),
где \( d_x \) - дифференциальный оператор, действующий на функцию \( f(x) \). Результатом действия дифференциального оператора на функцию является дифференциал этой функции. Таким образом, произведение дифференциала функции на дифференциал переменной может быть записано как \( d_x(f) \cdot dx \).
Практическое применение

Произведение дифференциала на дифференциал играет ключевую роль в математике, физике, экономике и других науках. В математике это понятие используется при решении дифференциальных уравнений, вычислении определенных интегралов и исследовании функций. В физике произведение дифференциалов помогает в описании изменений величин, нахождении скоростей, ускорений и других физических параметров. В экономике его применяют для моделирования процессов, связанных с предложением, спросом, ценами и другими важными показателями.
Значение в физике

В физике произведение дифференциала на дифференциал играет важную роль при решении различных задач. Оно может быть использовано для вычисления малых приращений величин в физических процессах. Например, при изучении изменения положения тела в пространстве или изменения скорости движения.
Произведение дифференциала на дифференциал позволяет строить математические модели, описывающие физические процессы с высокой точностью. Использование этого понятия помогает ученым анализировать изменения в системах и предсказывать результаты экспериментов.
Вопрос-ответ

Чему равно произведение дифференциала на дифференциал?
Произведение дифференциала на дифференциал не является определенной математической операцией. Математический смысл этого произведения зависит от контекста, в котором используется. В общем случае, произведение двух дифференциалов может рассматриваться как частный случай более общего понятия дифференциальной формы, но требует более конкретного определения для точного ответа.
Какие свойства имеет произведение дифференциала на дифференциал?
Произведение дифференциала на дифференциал обычно не обладает стандартными свойствами алгебраического умножения, такими как коммутативность, ассоциативность или дистрибутивность. Во многих случаях это произведение может рассматриваться как билинейная форма на пространстве дифференциальных форм и обладать свойствами, связанными с этим. Однако конкретные свойства произведения дифференциалов зависят от используемой математической структуры и задачи, поэтому требуют более точного контекста для полного ответа.



