Алгебраические выражения – это математические выражения, в которых используются числа, переменные и математические операции. Они являются основой алгебры и позволяют решать различные математические задачи.
Переменные в алгебраических выражениях представляют неизвестные величины, которые могут принимать различные значения. Они обозначаются буквами и используются для обобщения математических законов и формулирования уравнений.
Понимание основных понятий алгебраических выражений и переменных позволяет углубленно изучать математику и применять ее в решении практических задач в различных областях науки и техники.
Что такое алгебраическое выражение

Основные элементы алгебраического выражения

Алгебраическое выражение представляет собой комбинацию чисел, переменных и операций. В нем могут присутствовать следующие основные элементы:
- Числа: представляют собой константы. Например, 3, -5, 1/4.
- Переменные: обозначаются буквами и могут принимать различные значения. Например, x, y, a.
- Операции: включают арифметические операции (сложение, вычитание, умножение, деление) и другие математические операции (возведение в степень, извлечение корня).
Основные элементы алгебраического выражения взаимодействуют между собой с помощью операций, образуя математические выражения, которые можно упрощать и решать.
Что такое переменная в алгебре
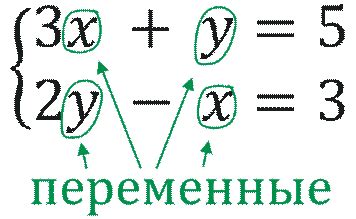
Свойства переменных в математике

Основные свойства переменных в математике:
1. Переменная может принимать любое значение из определенного диапазона.
2. При выполнении алгебраических операций с переменными результат также будет переменной.
3. Переменные могут быть использованы для представления неизвестных значений в уравнениях и системах уравнений.
4. Значение переменной может быть изменено или заменено другим значением в рамках математических выражений.
Упрощение алгебраических выражений

1. Уберите скобки: При упрощении алгебраического выражения вы можете начать с того, чтобы убрать скобки. Используйте свойства распределительности и ассоциативности, чтобы раскрыть скобки и объединить подобные члены.
2. Объедините подобные члены: После раскрытия скобок необходимо сложить или вычесть подобные члены в выражении. Подобные члены имеют одинаковые переменные и степени.
3. Упростите множители: Если в выражении есть множители, попробуйте упростить их, используя законы алгебры, такие как коммутативность и ассоциативность умножения.
Правильное упрощение алгебраического выражения поможет вам получить более компактную и понятную форму, что облегчит дальнейшие математические расчеты.
Примеры задач по переменным и выражениям

Пример 1: Найдите значение выражения 3a + 2b при a = 5 и b = 4.
Решение: Подставляем значения переменных: 3*5 + 2*4 = 15 + 8 = 23.
Пример 2: Упростите выражение 2x - 3y + x + 4y при x = 7 и y = 2.
Решение: Заменяем переменные на их значения: 2*7 - 3*2 + 7 + 4*2 = 14 - 6 + 7 + 8 = 23.
Пример 3: Найдите значение выражения (a + b) * 2 при a = 3 и b = 4.
Решение: Подставляем значения переменных: (3 + 4) * 2 = 7 * 2 = 14.
Практическое применение алгебры в жизни

Вопрос-ответ

Что такое алгебраическое выражение?
Алгебраическое выражение - это математическое выражение, составленное из переменных, чисел и операций сложения, вычитания, умножения и деления. Примером алгебраического выражения может служить 2x + 3y - 5.
Что такое переменная в алгебраических выражениях?
Переменная в алгебраических выражениях - это символ, обозначающий неизвестное число или значение. Она может принимать различные значения, и в алгебраическом выражении переменные обычно обозначаются буквами. Например, в выражении 2x + 3y переменные - это x и y.
Как упрощать алгебраические выражения?
Для упрощения алгебраических выражений используются свойства операций с числами, законы алгебры, раскрытие скобок, сокращение подобных членов и другие методы. Например, алгебраическое выражение (2x + 3) + 4x можно упростить, раскрыв скобки и объединив подобные члены, получится 6x + 3.



