Среди различных методов математической обработки чисел имеется одна, необычная и интересная техника, полностью основанная на принципе комбинирования и исключения. Речь идет о сумме чисел без учета их разницы. Отличие этого подхода заключается в том, что при сложении чисел мы рассматриваем только их общую сущность, игнорируя все отличия.
Суть этого метода заключается в том, что при объединении чисел мы не учитываем их взаимосвязь и различия, а смотрим только на их общие атрибуты. Это позволяет нам производить операции сложения с разными числами, не учитывая их конкретные значения. Например, вместо того чтобы складывать числа по-отдельности и получать результат по шагам, мы объединяем их в большую группу и фокусируемся на их итоговых характеристиках.
Примером такой суммы чисел без учета их разницы может служить задача, в которой требуется найти общую сумму всех чисел от 1 до 10. Вместо того чтобы складывать числа постепенно, можно объединить их в пары, игнорируя их конкретное значение и рассчитывая только на общую сумму. Например, можно объединить 1 и 10, 2 и 9, 3 и 8 и так далее, в итоге получив пять пар чисел, каждую из которых можно сложить, игнорируя их сравнения и разности. Таким образом, мы можем быстро и точно рассчитать сумму всех чисел от 1 до 10.
Основные принципы расчета суммы значений без учета их различий
В данном разделе мы рассмотрим основные принципы и подходы к расчету суммы значений, не учитывая их различия между собой.
Мы изучим способы объединения числовых величин, исходя из общего свойства, и покажем каким образом можно определить суммарное значение набора чисел, исключая их взаимные различия.
При расчете суммы чисел без учета их разницы, необходимо уделить внимание подобным значениям, которые по своей сути являются схожими или сопоставимыми. Для этого мы будем применять различные методы группировки и анализа, включая агрегирование, суммирование и усреднение значений.
Такой подход позволяет нам выделить общие характеристики набора чисел и определить их сумму, исключая разницу между ними.
Далее мы рассмотрим конкретные примеры, иллюстрирующие применение данных принципов в различных сферах, таких как экономика, статистика и наука. Мы проанализируем эти примеры и подробно рассмотрим их результаты, демонстрируя важность и практическую применимость принципов расчета суммы чисел без учета разницы.
Значимость суммирования числовых значений без учета их вычитания в области математики и физики

Исследование значения конкретного числа, путем его суммирования без учета действия вычитания, представляет собой важную аспект в области как математики, так и физики. Этот подход позволяет нам рассмотреть взаимосвязь между их количественными свойствами и создать основу для дальнейших вычислений и анализа.
Такой подход предоставляет возможность узнать общую суть числовых значений, а также способствует расширению понимания того, как обрабатывается информация в математическом и физическом контексте. Он может быть использован для определения принципов моделирования и прогнозирования различных физических процессов.
На практике, принцип суммирования чисел без учета вычитания широко используется в таких областях, как статистика, теория вероятности и анализ данных. Например, в математике это может быть полезным при вычислении среднего значения, расчете площади под кривой или определении статистических закономерностей.
Физика также использует этот принцип для изучения законов сохранения энергии, массы и импульса. Это позволяет исследовать взаимодействие между объектами и процессы, происходящие в физическом мире. Суммирование числовых значений без учета их разницы является необходимым инструментом для выявления общих закономерностей и определения важных параметров в физических экспериментах и исследованиях.
Примеры использования суммы числовых значений без учета их разницы в реальной жизни

- Финансовый анализ: использование суммы чисел без разницы позволяет оценить финансовое состояние компании, сравнивая общую сумму доходов и расходов, не учитывая детали их разделения. Этот метод позволяет получить общую картину и определить, какие аспекты требуют дополнительного изучения и анализа.
- Статистические исследования: для обработки больших объемов данных и выявления общих тенденций можно использовать сумму числовых значений без учета их разницы. Например, при анализе социальных исследований можно определить общее количество респондентов, не фокусируясь на отдельных атрибутах их характеристик. Это упрощает процесс обработки информации и выявления общих трендов.
- Управление проектами: при планировании и контроле выполнения проектов можно использовать сумму чисел в рамках определенных этапов или задач. Это позволяет установить общую продолжительность выполнения работ без учета их деталей, что помогает в определении критических моментов и распределении ресурсов.
Таким образом, сумма числовых значений без учета их разницы может быть полезным инструментом в различных областях, где требуется общая оценка и анализ данных. Этот принцип позволяет сосредоточиться на общей картине и выделить ключевые аспекты, сокращая время и затраты на детальный анализ каждого отдельного значения.
Подходы к вычислению суммы числовых значений без учета их различий в различных научных областях
Каждая научная дисциплина обладает своими собственными методами и подходами к решению задач, связанных с вычислением суммы числовых значений. В процессе исследования различных научных отраслей, от математики до физики и экономики, сложилось множество подходов к расчету суммы чисел без учета их разницы. Эти методы определяются спецификой дисциплины и контекстом проблемы, которую необходимо решить.
В математике, например, одним из подходов является использование арифметических операций для определения общей суммы числовых значений. Также существуют методы, основанные на упорядочивании чисел, создании числовых рядов или использовании формул для расчета суммы определенного ряда чисел.
В физике и других естественных науках, рассмотрение суммы числовых значений может быть связано с измерениями и обработкой данных. Здесь широко применяются статистические методы, включая расчет средних, медианы или суммы значений в пределах конкретного интервала.
В экономической науке, важной задачей является расчет суммарной стоимости или доходности, не учитывая отдельные различия. Это может быть основано на использовании арифметических операций, пропорций или расчета средних значений.
В различных областях научного исследования, существует множество других подходов к вычислению суммы числовых значений без учета их различий, основанных на уникальной специфике каждой дисциплины и целях исследования.
Доказательство эффективности применения суммы числовых значений без учета их различий в специфических задачах

Рассмотрим подход, основанный на идее вычисления суммы числовых значений без учета их разницы, и его эффективное применение в ряде конкретных задач. Этот метод позволяет упростить анализ данных и получить достоверные результаты, минимизируя время и усилия, затрачиваемые на их обработку.
Основной принцип этого подхода заключается в исключении различий между числовыми значениями и фокусировке на их общей сумме. Посредством этого мы можем выявить общие закономерности и тенденции, что позволяет принимать обоснованные решения и выполнять анализ на более высоком уровне.
Конкретные примеры применения этой стратегии включают в себя решение задач, связанных с прогнозированием трендов на рынке, оценкой финансовой устойчивости компаний и планированием бюджета. Во всех этих сценариях вычисление суммы числовых значений без учета разницы играет ключевую роль в обнаружении общих шаблонов и определении наиболее вероятных сценариев развития событий.
Алгоритмы для вычисления суммы чисел без учета их разницы: примеры и решения
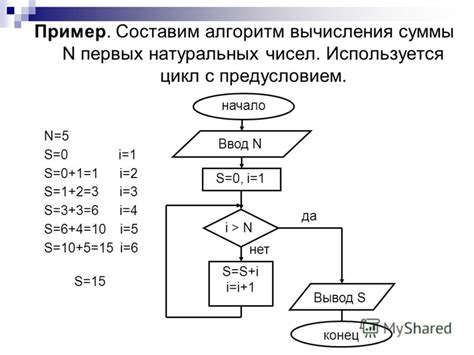
В данном разделе мы рассмотрим различные алгоритмы, которые позволяют вычислять сумму чисел, не учитывая их разницы. При использовании этих алгоритмов, принципы расчетов основываются на идеях, которые позволяют объединять числа, чтобы получить их общую сумму без учета их разницы.
Рассмотрим первый алгоритм: алгоритм суммы по формуле арифметической прогрессии. Он основывается на свойствах арифметической прогрессии и позволяет эффективно вычислять сумму чисел, представленных в виде последовательности.
- Шаг 1: Определите начальный и конечный элементы последовательности чисел.
- Шаг 2: Вычислите разницу между начальным и конечным элементами.
- Шаг 3: Вычислите количество элементов в последовательности, вычитая начальный элемент из конечного и добавив 1.
- Шаг 4: Примените формулу арифметической прогрессии для вычисления суммы чисел: S = (n / 2) * (2a + (n - 1)d), где S представляет сумму, n - количество элементов, а и d - соответственно первый элемент и разность между элементами последовательности.
Рассмотрим второй алгоритм: алгоритм суммирования по парам чисел. Он заключается в суммировании чисел попарно без учета их разницы. Данный алгоритм основывается на следующих шагах:
- Шаг 1: Разбейте исходные числа на пары. Если количество чисел нечетное, последнее число будет представлено одиночно.
- Шаг 2: Для каждой пары чисел выполните сложение двух чисел и получите сумму.
- Шаг 3: Если остается одиночное число, добавьте его к общей сумме.
- Шаг 4: Получите окончательную сумму чисел без учета их разницы.
Таким образом, в данном разделе мы рассмотрели простые алгоритмы для вычисления суммы чисел без учета их разницы. Алгоритмы, основанные на формуле арифметической прогрессии и суммировании чисел по парам, позволяют эффективно решать задачи, связанные с вычислением общей суммы чисел.
Роль сумм числовых значений без учета их разницы в статистических исследованиях

В статистических исследованиях широко используются различные методы анализа данных, включая анализ сумм числовых значений без учета их разницы. Этот подход позволяет выяснить общий тренд или среднее значение наблюдаемых данных, минуя детали их разброса или отклонений.
Понимание особенностей использования данного подхода в статистических исследованиях является ключевым для правильной интерпретации результатов и принятия соответствующих решений. Важно учитывать, что сумма числовых значений без учета их разницы может дать общую картину или оценку, но не учитывает деталей или отклонений между отдельными наблюдениями.
Метод суммирования числовых значений без учета их разницы может быть полезен, когда требуется быстро оценить общую тенденцию или среднюю величину наблюдаемых данных, не заботясь о различиях между ними. Например, в маркетинговых исследованиях такой подход может использоваться для анализа совокупных продаж или общего объема продукции без учета вариаций между отдельными товарами или клиентами.
Однако, необходимо быть осторожным при использовании суммы числовых значений без учета их разницы в статистических исследованиях. Этот метод может привести к упущению важных деталей или отклонений, которые могут быть значимыми для требующего более детального анализа. Поэтому рекомендуется совмещать данный подход с другими методами и учитывать вариации и отклонения при интерпретации результатов.
- Сумма числовых значений без учета их разницы важна в статистических исследованиях
- Метод полезен для выявления общего тренда или среднего значения
- Предоставляет общую оценку, но не учитывает детали или отклонения между отдельными наблюдениями
- Подход может быть применен в маркетинговых исследованиях или других областях для оценки общей тенденции
- Но требуется осторожность и дополнительные методы анализа для полного понимания данных
Роли суммирования числовых данных без учета их различия в финансовом анализе и прогнозировании

В современном финансовом анализе и прогнозировании, сумма числовых показателей без учета их разницы играет важную роль в определении общей динамики и тенденций. Этот подход основывается на концепции объединения значений в целях получения общей картины и оценки текущего состояния, а также прогнозирования будущих изменений.
Стремление понять и проанализировать финансовую ситуацию организации или рынка может потребовать сводных данных, которые подчеркивают суммарное влияние числовых показателей, независимо от их различий. Единая сумма чисел без учета их разницы позволяет выявить общие закономерности, скрытые отдельными значениями.
В финансовом анализе, например, сумма доходов, расходов, активов или пассивов может дать ценную информацию о состоянии компании в целом, позволяя оценить ее финансовую устойчивость, эффективность и потенциал для роста. Аналогично, суммирование финансовых показателей рынка или отрасли может помочь в прогнозировании общего направления его развития и выявлении сильных и слабых сторон.
Более того, суммирование числовых данных без учета их разницы позволяет учесть вклад каждого показателя в общую картину. Это позволяет выделить ключевые факторы, оказывающие наибольшее влияние на итоговый результат, и объединить их в целях выявления общих закономерностей и трендов.
Одной из основных преимуществ данного подхода является возможность упрощения анализа числовых данных, исключая влияние отдельных разностей между числами. При использовании суммы чисел без учета разницы, мы сосредотачиваемся на общей сумме значений, что позволяет нам получить более ясное представление о структуре данных и их распределении.
В различных областях применения, таких как экономика, статистика, финансы и т. д., использование этой концепции может упростить анализ тенденций и трендов, исключая возможные искажения, вызванные различными разностями. Например, в экономике сумма доходов без учета продаж может дать нам общую картину о финансовом состоянии компании, не углубляясь в детали различных источников доходов.
Другое преимущество использования суммы чисел без учета разницы заключается в возможности сравнения разных наборов данных. При использовании этого подхода мы можем сравнивать общую сумму значений в разных группах или периодах времени, не учитывая конкретные разности между значениями. Это позволяет нам выявлять существенные различия и сопоставлять общие тренды в разных контекстах.
| Таблица преимуществ использования суммы чисел без учета разницы |
|---|
| Упрощение анализа числовых данных |
| Исключение искажений, вызванных разностями |
| Лучшая общая картина о структуре и распределении данных |
| Возможность сравнения разных наборов данных |
| Выявление существенных различий и сопоставление общих трендов |
Вопрос-ответ

Как вычислить сумму чисел без их разницы?
Для вычисления суммы чисел без их разницы нужно сложить все числа и вычесть из полученной суммы их разницу.
Почему нужно вычитать разницу между числами?
Вычитание разницы между числами позволяет исключить влияние различий в значениях чисел на итоговую сумму. Таким образом, мы получаем сумму только самих чисел, а не их различий.
Какие принципы используются при вычислении суммы чисел без их разницы?
Основным принципом является сложение всех чисел с последующим вычитанием их разницы. Также необходимо учитывать знаки чисел при выполнении сложения и вычитания.
Можете привести пример вычисления суммы чисел без их разницы?
Конечно! Допустим, у нас есть числа 5, 3 и 8. Для вычисления суммы без разницы мы сложим эти числа: 5 + 3 + 8 = 16. Затем вычтем их разницу: 16 - (8 - 5) = 13. Таким образом, сумма чисел без их разницы равна 13.
Можно ли применять этот метод вычисления суммы для любых чисел?
Да, этот метод применим для любых чисел. Важно только правильно выполнить сложение и вычитание, а также учесть знаки чисел. Сумма чисел без их разницы будет правильно вычислена в любом случае.



