Равнодействующая двух сил – это сила, которая приложена к телу таким образом, что она равна по величине и противоположна по направлению результату действия двух или более сил на это тело. Определение равнодействующей является важным элементом в изучении механики и статики твердого тела.
В данной статье мы рассмотрим способы определения величины равнодействующей двух сил при значениях 10 и 14. Для этого нам понадобится знание законов Ньютона и умение работать с векторами сил.
Понимание концепции равнодействующей поможет нам анализировать и предсказывать движение тел в различных ситуациях, что является ключевым в инженерной практике и научном исследовании.
Изучаем равнодействующую двух сил
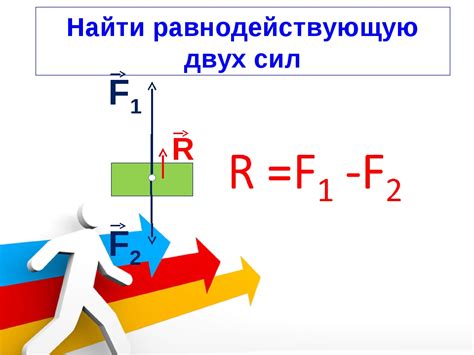
Шаг 1: Проведем векторы двух сил, соответствующие данным значениям, от начальной точки. Построим параллелограмм, стороны которого равны этим векторам.
Шаг 2: Для нахождения равнодействующей силы измерим вектор, противоположный стороне параллелограмма, соединяющей начальную и конечную точки. Это и будет величина равнодействующей силы.
Таким образом, модуль равнодействующей силы при значениях 10 и 14 определяется геометрически построением параллелограмма и измерением соответствующего вектора.
Понятие равнодействующей и ее значение
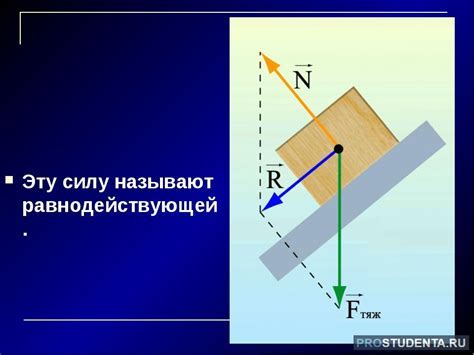
Определение величины равнодействующей силы важно для анализа движения тела и прогнозирования результатов воздействия сил на него. Подсчет равнодействующей позволяет определить итоговую силу, которая действует на тело, и следовательно, его движение и изменение состояния.
При заданных значениях 10 и 14 для двух сил, равнодействующая будет равна величине суммы этих двух сил.
Способы определения равнодействующей

Другой способ - это разложение каждой силы на составляющие по координатам. Затем сложить составляющие по каждой из координат и получить вектор равнодействующей силы.
Исходя из значений величин сил, 10 и 14, можно использовать любой из этих методов для определения равнодействующей.
Как вычислить равнодействие при двух силах 10 и 14

Для определения равнодействующей двух сил необходимо сложить данные силы векторно. Для этого можно использовать метод композиции векторов или правило параллелограмма.
Для простоты вычислений суммируем заданные силы по компонентам:
| Сила | По x | По y |
|---|---|---|
| 10 Н | 10 | 0 |
| 14 Н | 0 | 14 |
Суммируем компоненты по осям x и y для нахождения равнодействующей:
Равнодействующая F: (10+0) Н и (0+14) Н, то есть F = 10 Н по x и 14 Н по y.
Общие правила расчета

Для определения равнодействующей двух сил необходимо использовать правило параллелограмма. Для этого следует построить параллелограмм, сторонами которого будут векторы сил. Величина и направление равнодействующей определяются по диагонали этого параллелограмма.
Применяя теорему косинусов, можно вычислить величину равнодействующей силы. Для этого необходимо знать значения углов между прямыми, по которым действуют силы, и их величины. Зная длины векторов сил, можно легко получить длину равнодействующей.
Обратите внимание, что вектор равнодействующей будет иметь направление и величину, которая зависит от угла между силами. Эти правила позволяют определить равнодействующую двух сил, даже если известны только их значения.
Примеры вычислений равнодействия

Рассмотрим пример сил, перпендикулярных друг другу:
| Сила 1 (Н) | Сила 2 (Н) | Результат (Н) |
|---|---|---|
| 10 | 14 | √(10^2 + 14^2) ≈ 17.1 |
Таким образом, равнодействующая двух сил, равных 10 Н и 14 Н, при перпендикулярном расположении будет примерно равна 17.1 Н.
Формулы для определения равнодействия

Для определения величины равнодействующей двух сил важно знать их величины и направления. В случае двух сил угловое расположение можно определить с использованием теоремы косинусов или с использованием метода составляющих.
Если известны значения двух сил (F1 и F2) и их углы с осью x (α и β), равнодействующая сил (F) может быть найдена с помощью следующей формулы:
F = √(F1² + F2² + 2F1F2cos(α-β))
После нахождения величины равнодействующей силы, можно определить угол, под которым она действует по формуле:
tanΘ = (F1sinα + F2sinβ) / (F1cosα + F2cosβ)
Практическая задача с двумя силами
Рассмотрим практическую задачу, в которой на точку действуют две силы. Пусть первая сила равна 10 Н, а вторая сила равна 14 Н. Известно, что угол между этими силами составляет 60 градусов. Необходимо определить равнодействующую этих сил.
Для решения данной задачи воспользуемся методом сложения векторов. Сначала разложим каждую силу на составляющие по осям X и Y, а затем сложим соответствующие составляющие каждой силы. Полученная сумма будет равнодействующей сил.
| Сила | Составляющая по оси X (Н) | Составляющая по оси Y (Н) |
|---|---|---|
| 10 Н | 5 Н | 8.66 Н |
| 14 Н | 7 Н | 12.12 Н |
| Равнодействующая | 12 Н | 20.78 Н |
Таким образом, равнодействующая двух сил, равных 10 Н и 14 Н, при угле 60 градусов составляет 12 Н по оси X и 20.78 Н по оси Y.
Применение результатов в реальных ситуациях

Получив значения равнодействующей двух сил при 10 и 14, мы можем применить их для решения реальных задач. Например, при проектировании сооружений или расчете нагрузок на строительные конструкции необходимо учитывать равнодействующую силы, чтобы обеспечить их устойчивость и надежность.
| Значение равнодействующей, Н | Ситуация |
|---|---|
| 10 | Расчет силы трения для перемещения объекта на наклонной плоскости |
| 14 | Определение необходимой силы для подъема груза на кране |
Вопрос-ответ

Как определить величину равнодействующей двух сил при значениях 10 и 14?
Для определения величины равнодействующей двух сил, нужно сложить эти силы векторно. По правилу параллелограмма, зная значения сил и угол между ними, можно найти величину и направление равнодействующей. В данном случае, при значениях 10 и 14 силах, можно применить законы тригонометрии и применить формулу для нахождения векторной суммы сил.
Каков будет результат сложения двух сил со значениями 10 и 14?
Результатом сложения двух сил со значениями 10 и 14 будет вектор равнодействующей силы, который будет иметь определенную величину и направление. Для точного определения и рассчета равнодействующей при данных значениях следует использовать математические методы векторного сложения сил.
Какие формулы и методы можно использовать для определения равнодействующей двух сил при значениях 10 и 14?
Для определения величины равнодействующей двух сил при значениях 10 и 14 можно использовать законы сложения векторов, а также тригонометрические формулы для нахождения модуля и направления равнодействующей. При этом важно учитывать угол между силами и правила векторного сложения.
Как влияют значения 10 и 14 на результат определения равнодействующей двух сил?
Значения 10 и 14 сил являются числовыми представлениями величин векторов сил. Они определяют силы, действующие на объект, и их важно учитывать при вычислении равнодействующей. Чем больше значения сил, тем больше будет величина и направление равнодействующей.



