Когда мы говорим о природе, мы представляем себе чудесную гармонию и уникальную организацию живых существ. Однако, для полного понимания этого богатого мира, необходимо рассмотреть его также с точки зрения математики и графов. В этой статье мы представим особый взгляд на наше растительное царство: рассмотрение деревьев в качестве двудольных графов и потенциальные ограничения, с которыми мы можем столкнуться.
Древесные структуры как сказочные лабиринты
Представьте их ветви, около которых петляют змеи и прячутся животные, а также их корни, проникающие в глубины земли, словно шальные путники. Внимательное изучение деталей позволит нам открыть абстрактную красоту, скрытую в этой божественной симфонии.
Таким образом, двудольные графы являются мощным инструментом для анализа деревьев и других растительных образований.
Изучение роли графов в информатике

Одной из основных идей графов является представление объектов и связей между ними в виде вершин и ребер. Вершины представляют объекты, а ребра - связи или отношения между этими объектами. Графы позволяют упорядочить и классифицировать информацию, а также выявлять закономерности и связи в сложных системах.
Изучение графов в информатике помогает разработчикам создавать эффективные алгоритмы и принимать решения на основе анализа комплексных данных. Они широко используются в области искусственного интеллекта, оптимизации, компьютерного зрения и многих других областях. Понимание и применение графов в информатике имеет большое значение для развития современных технологий и улучшения жизни людей.
Основные понятия и определения

Структура - одно из важных понятий, которое описывает взаимосвязанные компоненты дерева. Структура дерева определяет его иерархическое устройство, а также возможности для организации и доступа к его элементам.
Узел - основной элемент дерева. Каждый узел имеет определенные свойства и может содержать информацию или ссылки на другие узлы. Узлы дерева могут быть различных типов и выполнять определенные функции.
Ветвь - связь между двумя узлами дерева. Ветви отображают отношения между узлами и определяют порядок расположения элементов в дереве. Каждая ветвь имеет начальный и конечный узлы, которые могут быть связаны друг с другом напрямую или через другие промежуточные узлы.
Корень - особый узел, который является начальным элементом всего дерева. Корень не имеет родителей, но может иметь несколько дочерних узлов. Он является основой для всей структуры дерева и определяет его иерархическую организацию.
Листья - узлы дерева, которые не имеют дочерних элементов. Листья являются конечными элементами и несут некоторую информацию или выполняют определенные функции. Они представляют собой важные точки данных в дереве и могут быть использованы для решения различных задач.
Важно понимать эти основные понятия и определения для дальнейшего изучения двудольного графа, основанного на дереве. Они обеспечивают базовую терминологию и помогают описывать и анализировать строение и связи внутри этой структуры.
Применение графов в задачах: поиск и анализ связей
В данном разделе мы рассмотрим широкий спектр задач, в которых графы применяются для поиска и анализа связей между объектами или явлениями. Графы выступают в роли универсального инструмента, который позволяет эффективно изучать различные типы взаимосвязей и их свойства. Благодаря универсальности графов, мы можем применять их для решения задач в различных областях, таких как биология, социология, информатика и т.д.
Одной из наиболее известных задач, где графы используются, является задача о поиске кратчайшего пути. Благодаря графовым алгоритмам, можно находить оптимальные пути в сетях связей разного рода, таких как транспортные системы, компьютерные сети или дорожные сети. Графы также позволяют исследовать структуру социальных сетей, анализировать связи между участниками и определять ключевых игроков или сообщества внутри сети. Это лишь некоторые примеры применения графовых алгоритмов в задачах поиска и анализа связей.
Более того, графы могут быть использованы для моделирования и повышения эффективности различных процессов. Например, в биологии графы применяются для моделирования молекулярных структур, метаболических путей и генных сетей. В информатике графы используются для оптимизации работы алгоритмов и поиска оптимальных решений. Также графы широко применяются в лингвистике и обработке естественного языка для анализа и классификации текстов, построения семантических моделей и решения других задач, связанных с языковыми структурами и взаимодействиями.
Применение графов в задачах позволяет нам более глубоко понять структуры и связи между объектами в различных областях знаний. Графы предоставляют нам удобный и эффективный способ моделирования и анализа сложных систем, открывая возможности для решения сложных задач, оптимизации процессов и нахождения новых знаний. От простых поисковых алгоритмов до сложных моделей и алгоритмов машинного обучения, графы являются неотъемлемой частью современной науки и технологий.
Специальные свойства древовидного графа
Различные исследователи и ученые отмечают важность древовидного графа и его специфических черт в решении задач, требующих организации и структурирования данных. Одним из наиболее примечательных свойств дерева является его способность иерархически представлять информацию, позволяя упорядочить и связать различные элементы между собой.
Кроме того, дерево обладает свойством единственного пути между любыми двумя вершинами, что позволяет эффективно организовывать и хранить данные. Также стоит отметить, что дерево обеспечивает удобный доступ к информации, так как каждая вершина имеет своих потомков и может быть быстро обнаружена и проанализирована.
Следует отметить, что дерево эффективно применяется в информационных системах для представления иерархических структур данных, таких как файловые системы и организация баз данных. Благодаря своим специальным свойствам, дерево является удобным и надежным способом представления сложной информации и позволяет эффективно обрабатывать ее.
Структура и характеристики дерева
Данный раздел будет посвящен изучению основных структурных компонентов и характеристик дерева. Мы рассмотрим различные свойства, которые отличают дерево от других графовых структур и определяют его специфику и функциональность.
Начнем с анализа структуры дерева. В рамках данного раздела будут рассмотрены три ключевых элемента, на которых базируется структура дерева: корень, вершины и ребра. Каждый из этих компонентов играет важную роль в формировании связей и организации информации внутри дерева.
Затем мы перейдем к изучению характеристик дерева, которые определяют его своеобразие и позволяют использовать его в разных областях. Будут рассмотрены такие важные аспекты, как глубина дерева, высота дерева, степень вершины, ширина дерева и уровень вершины. Каждая из этих характеристик имеет свой функциональный смысл и может быть использована для решения конкретных задач.
Одной из ключевых особенностей дерева является его иерархическая структура, которая позволяет организовать информацию в виде древовидной иерархии. Мы рассмотрим примеры реального мира, где дерево используется в качестве модели данных, и объясним, почему дерево является эффективным инструментом для таких задач.
Применение деревьев в различных сферах

Информационные технологии В сфере информационных технологий деревья являются одной из важных составляющих различных алгоритмических и структурных задач. Они применяются для организации иерархических структур данных, таких как файловые системы, деревья поиска и структуры данных для хранения и манипулирования сетевыми данными. Деревья также используются в алгоритмах сортировки, обхода графов и поиска оптимальных решений. | Биология В биологии деревья используются для классификации живых организмов. Филогенетические деревья позволяют представлять исторические связи и эволюционные отношения между видами. Клеточные деревья позволяют анализировать иерархическую структуру организмов, например, в генетических исследованиях. Деревья также находят применение в анализе генных последовательностей и прогнозировании эволюционной истории живых систем. |
Генеалогия В генеалогии деревья используются для представления семейных связей и построения родословных деревьев. Они позволяют отслеживать предки, потомков и их связи между собой. Деревья в генеалогии могут также использоваться для анализа генетической информации и выявления наследственных характеристик у исследуемых семейных линий. | Другие области Кроме того, деревья находят применение во многих других областях, таких как логистика, финансы, социология и многие другие. Они могут быть использованы для моделирования и анализа этих областей, представления иерархических структур и принятия оптимальных решений в сложных задачах. |
Раздел: Парные графы
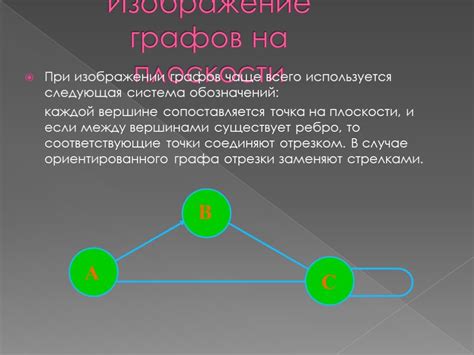
Парные графы характеризуются особым разделением вершин на два непересекающихся множества. Данная особенность открывает широкие возможности для исследования и анализа взаимосвязей между вершинами.
В этом разделе мы рассмотрим базовые понятия и свойства парных графов, а также углубимся в их математическую модель и алгоритмы. Будет рассмотрена
структура парного графа и эффективные способы его представления и обработки. Также будет рассмотрено применение парных графов в различных областях, от биологии до социологии, чтобы продемонстрировать широкий спектр их применения.
Цель этого раздела - освоить основы парных графов и понять, как этот тип графов может быть использован для анализа и моделирования различных систем и социальных связей.
Определение и свойства двудольных графов

Этот раздел посвящен изучению концепции двудольных графов и их основным свойствам, которые играют важную роль в различных областях науки и инженерии. В рамках анализа таких графов мы обратим внимание на их определение и структурные особенности, позволяющие классифицировать их и применять для решения разнообразных задач.
Двудольный граф – это модель, которая состоит из двух непересекающихся множеств вершин, таких что между любыми двумя вершинами определенного множества нет ребра. Такая структура позволяет удобно представлять различные взаимоотношения и связи между элементами двух наборов. Ключевой характеристикой двудольных графов является их разделение на две части – левую и правую доли, которые определяются внутренними связями и зависимостями между вершинами.
Основные свойства двудольных графов позволяют использовать их для решения различных задач. Например, они широко применяются в информатике для моделирования и анализа ситуаций, где необходимо учесть несколько наборов данных или взаимосвязей. Важно отметить, что для данного типа графов существует алгоритм проверки двудольности, который позволяет определить, можно ли разбить вершины на две доли, так чтобы ребра соединяли только вершины из разных долей.
В дальнейшем мы рассмотрим подробнее свойства и применение двудольных графов, а также решение практических задач с их помощью.
Применение параллельных графов в задачах планирования и оптимизации
Ключевыми преимуществами применения двудольных графов в задачах планирования и оптимизации являются:
- Возможность представления сложных систем в виде наглядного графа, в котором вершины первой доли соответствуют определенным заданиям или задачам, а вершины второй доли - ресурсам или ограничениям;
- Возможность учитывать зависимости и взаимосвязи между задачами и ресурсами, что позволяет более точно оптимизировать процессы и распределять ресурсы;
- Возможность проведения анализа и симуляции различных сценариев, что позволяет оценить эффективность планов и выбрать наилучший вариант;
- Возможность применения различных алгоритмов оптимизации для достижения наилучших результатов в задачах планирования и управления.
Одним из примеров практического применения двудольных графов в задачах планирования является оптимизация производственных процессов. Задача состоит в максимизации эффективности и минимизации затрат через оптимальное расписание на производстве. Представление данной задачи в виде двудольного графа позволяет учесть все производственные операции и ресурсы, а также их взаимосвязи и зависимости, что помогает найти наилучший план действий.
Анализ структуры дерева в контексте двудольного графа
В данном разделе мы будем рассматривать основные принципы и проблемы, связанные с использованием деревьев в качестве двудольных графов.
Уникальная особенность дерева в том, что оно может быть описано как совокупность вершин и ребер, представляющих собой сильно связанные узлы и их взаимосвязи. В контексте двудольного графа, эти связи выстраиваются между разделением дерева на две независимые группы вершин, которые не имеют общих ребер внутри своей группы.
- Возможность представления дерева как двудольного графа позволяет использовать разнообразные алгоритмы и методы, разработанные для работы с двудольными графами. Это может быть полезно, например, для определения наличия путей или циклов между двумя заданными вершинами.
- Однако, существуют определенные ограничения и сложности при применении концепции двудольных графов к структуре дерева. Некоторые алгоритмы, разработанные для работы с двудольными графами, могут быть неэффективными или неприменимыми в контексте деревьев.
- Важно учитывать, что не все деревья могут быть представлены как двудольные графы. Некоторые структуры деревьев имеют специфические связи между вершинами, которые не могут быть разделены на две независимые группы. При использовании алгоритмов, разработанных для двудольных графов, необходимо учитывать эти ограничения и подходить к анализу дерева с учетом его уникальных особенностей.
Вопрос-ответ

Что такое двудольный граф?
Двудольный граф - это граф, вершины которого можно разделить на две непересекающиеся группы таким образом, что каждое ребро соединяет вершину одной группы с вершиной другой группы.
Как можно представить дерево в виде двудольного графа?
Для представления дерева в виде двудольного графа, можно разделить вершины дерева на две группы, так чтобы все ребра соединяли вершины из разных групп. Одну группу можно выбрать как корень дерева, а другую группу - как все остальные вершины дерева.
Какие ограничения могут быть у дерева как двудольного графа?
Ограничениями для дерева как двудольного графа могут быть следующие: количество вершин в каждой группе должно быть примерно равным, каждая вершина должна быть соединена ребром с вершиной из другой группы, и не должно быть циклов в графе.
Какова практическая польза представления деревьев в виде двудольных графов?
Представление деревьев в виде двудольных графов может быть полезным при решении определенных задач. Например, это может помочь в оптимизации процесса поиска или обхода дерева, а также при выполнении алгоритмов, основанных на свойствах двудольных графов.



