Определение корней уравнения является важным этапом в изучении математики. Однако не всегда уравнение имеет решение. Существует несколько признаков, по которым можно определить, что уравнение не имеет корней. Рассмотрим подробный анализ этих признаков.
Дискриминант - это ключевой показатель при определении количества корней уравнения. Если дискриминант меньше нуля, то уравнение не имеет действительных корней. Этот случай можно наблюдать при решении квадратного уравнения.
Кроме того, графический метод позволяет визуально определить отсутствие корней уравнения. Построение графика функции позволяет увидеть, что кривая не пересекает ось абсцисс, что говорит о том, что уравнение не имеет корней.
Определение отсутствия корней в уравнении

Уравнение не имеет корней, если его дискриминант меньше нуля.
Дискриминант уравнения \( ax^2 + bx + c = 0 \) определяется по формуле \( D = b^2 - 4ac \).
Если \( D
В случае отрицательного дискриминанта уравнение имеет комплексные корни, которые можно найти с помощью формулы:
\( x_1 = \frac{-b + \sqrt{-D}}{2a} \)
\( x_2 = \frac{-b - \sqrt{-D}}{2a} \).
Понятие уравнения без корней

Уравнение не имеет корней, если его график не пересекает ось абсцисс, то есть не существует значения переменной, при котором уравнение равно нулю. Это означает, что уравнение не имеет решений в действительных числах. Однако, уравнение может иметь комплексные корни, если решение лежит в комплексной плоскости.
Какие случаи возникают

Уравнение не имеет корней в следующих случаях:
1. Дискриминант меньше нуля: Если дискриминант ∆ меньше нуля (∆ < 0), то уравнение не имеет действительных корней, так как квадратный корень из отрицательного числа не существует.
2. Уравнение не приводится к квадратному виду: Если уравнение не является квадратным (то есть степень уравнения больше двух), то оно не имеет корней в рамках действительных чисел.
3. Уравнение противоречиво: Если при решении уравнения возникают нелогичные или противоречивые утверждения, то это означает, что уравнение не имеет корней в области действительных чисел.
Анализ дискриминанта
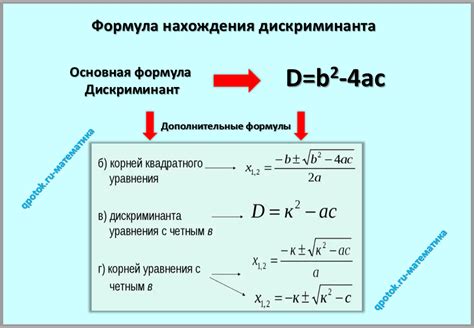
Для определения количества корней уравнения необходимо проанализировать дискриминант.
Если дискриминант положителен (D > 0), то уравнение имеет два различных корня.
Если дискриминант равен нулю (D = 0), то уравнение имеет один корень кратности два.
Если дискриминант отрицателен (D
Таким образом, проведя анализ дискриминанта, можно точно определить количество корней уравнения.
Теорема Виета

Пусть дано уравнение вида: ax^2 + bx + c = 0.
Тогда по теореме Виета:
- Сумма корней уравнения равна: x1 + x2 = -b/a.
- Произведение корней уравнения равно: x1 * x2 = c/a.
Таким образом, зная коэффициенты уравнения, мы можем вычислить сумму и произведение его корней без их явного нахождения.
Примеры решения уравнений

Пример 2: Рассмотрим уравнение 2x^2 + 5x + 3 = 0. Дискриминант D = 5^2 - 4*2*3 = 25 - 24 = 1. Поскольку D > 0, уравнение имеет два различных корня.
Пример 3: Рассмотрим уравнение x^2 + 2x + 1 = 0. Дискриминант D = 2^2 - 4*1*1 = 4 - 4 = 0. Уравнение имеет один корень x = -1.
Вопрос-ответ

Как определить, что у уравнения нет корней?
Уравнение не имеет корней, если его дискриминант отрицательный. Дискриминант равен b^2 - 4ac, где a, b, c - коэффициенты уравнения ax^2 + bx + c = 0. Если дискриминант меньше нуля, то уравнение не имеет действительных корней.
Что происходит, если дискриминант уравнения равен нулю?
Если дискриминант уравнения равен нулю, то уравнение имеет один корень. Такой случай называется уравнением с одним корнем кратности два. Корень определяется по формуле x = -b/(2a).
Может ли уравнение иметь два различных корня?
Да, уравнение может иметь два различных корня. Это происходит в случае, когда дискриминант положителен. В этом случае уравнение имеет два действительных корня, которые находятся по формуле x = (-b ± √D) / 2a, где D - дискриминант уравнения.



