В мире геометрии, где плотно переплетаются линии и углы, есть определенные закономерности, которые помогают нам понять взаимосвязь между различными фигурами. Одна из таких форм, пользующаяся особым вниманием, является квадрат – самая симметричная из всех многоугольников.
Когда мы обращаемся к квадрату, нам легко представить его четыре угла и стороны, но что насчет диагонали? Диагональ, это та линия, которая соединяет две несмежные вершины квадрата, и задаваться вопросом о ее симметрии – значит вложиться в хитрый парадокс.
Погрузимся в мир геометрических форм и проследим за тем, как взаимодействие сторон и углов квадрата влияет на величину его диагонали. Узнаем, является ли эта линия симметричной осью, которая делит квадрат на две идентичные части, и какие закономерности соединяют ее с другими элементами геометрии.
Роль линейных элементов в расположении фигуры

В данном разделе рассматривается роль особого типа линейных элементов в организации расположения геометрических фигур. Эти элементы играют важную роль в определении симметрии и гармоничности конструкции. Рассмотрим, каким образом линейные элементы могут внести симметрию в основу фигуры, придавая ей эстетическую привлекательность и уравновешенность.
- Линии стыка
- Границы
- Разделительные полосы
- Контурные линии
Линии стыка, являющиеся одним из главных элементов симметрии, образуют границы между компонентами фигуры и создают пространственные отношения между ними. Именно они придают фигуре гармоничную организацию и задают основные направления и симметрии. Границы, в свою очередь, определяют и дополняют эту симметрию, устанавливая равновесие и контролируя взаимное расположение частей фигуры.
Уникальной ролью разделительных полос является создание внутренней гармонии путем организации различных элементов и участков фигуры. Они служат границами, зонами пересечений или пространствами, придающими особый характер и симметрию в конструкции. Контурные линии, детализирующие форму, образуют дополнительные симметричные элементы, дополняющие и улучшающие общий эффект фигуры.
Свойства линии, соединяющей противоположные углы квадрата: фактические данные и практические примеры

Симметрия – это понятие, которое означает равные по форме, размеру или положению элементы, расположенные относительно определенной оси. В случае квадрата, его диагональ – это линия, которая проходит из одного угла в противоположный и делит фигуру на две равные половины. Данный раздел посвящен доказательству факта, что линия, соединяющая противоположные углы квадрата, является симметричной осью, а также представлению информации о практических примерах, подтверждающих это утверждение.
Одним из практических примеров является рассмотрение квадрата, изначально заданного вращением. Вращая фигуру на определенный угол, мы замечаем, что линия, соединяющая противоположные углы, остается неподвижной и сохраняет свою симметричность относительно других элементов квадрата. Этот пример наглядно иллюстрирует факт, что диагональ является симметричной осью и выполняет важную роль в структуре квадрата.
Неодинаковость одной линии внутри объекта

Привлекательность изучения таких линий заключается в особых чертах, которые подчеркивают Минусы данного объекта. Подобные отличия от остальных элементов позволяют получить новую перспективу на геометрические формы и их структуру.
Одним из аргументов в пользу несимметричности данной линии является дисбаланс в ее форме и размерах. В отличие от других элементов объекта, она обладает специфической конфигурацией, что сразу привлекает внимание и вызывает интерес у исследователей. Такое отличие делает данную линию уникальной и неповторимой в рамках геометрического объекта.
Принципиальное рассмотрение: аргументы в пользу или против симметричности диагонали квадрата
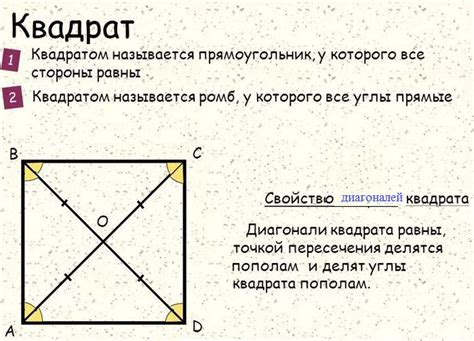
Аргументы в пользу симметричности:
| Аргументы против симметричности:
|
В итоге, споры о симметричности или несимметричности диагонали квадрата имеют основания существовать, так как аргументы сторонников и противников имеют свое обоснование. Несмотря на это, полное понимание природы квадрата и его особенностей может помочь найти ответ на данную дискуссию и выявить, какой из аргументов является более обоснованным и логичным.
Вопрос-ответ

Что такое диагональ квадрата?
Диагональ квадрата - это отрезок, соединяющий противоположные вершины квадрата.
Является ли диагональ квадрата симметричной осью?
Да, диагональ квадрата является симметричной осью. Это означает, что при отражении фигуры относительно этой оси, она сохраняет свою форму.
Какое свойство имеет диагональ квадрата?
Диагональ квадрата обладает свойством быть равнобедренной и равноугольной. Это означает, что она делит квадрат на два равных прямоугольных треугольника и образует прямой угол с каждой стороной квадрата.
Существует ли разница между диагональю квадрата и его сторонами?
Да, диагональ квадрата и его стороны имеют разные длины. Длина диагонали квадрата равна в корне из двух раз больше длины его стороны.
Есть ли какие-либо особые свойства, для которых диагональ квадрата не является симметричной осью?
Нет, для всех геометрических свойств и операций, связанных с квадратом, диагональ является симметричной осью.



