Окружность, вписанная в квадрат, является одной из классических геометрических фигур, привлекающей внимание своей симметрией и простотой. Одним из ключевых параметров такой конструкции является диаметр вписанной окружности. В данной статье мы рассмотрим формулу для расчёта диаметра вписанной в квадрат окружности и рассмотрим примеры его применения.
Для начала стоит отметить, что диаметр вписанной в квадрат окружности равен стороне этого квадрата. Это свойство может использоваться для установления добавочных связей в геометрических задачах, а также для выполнения точных измерений. Однако, для более сложных случаев, когда необходимо точное значение диаметра, применяется специальная формула.
Что такое диаметр вписанной окружности?

Определение и основные понятия

Для расчета диаметра вписанной в квадрат окружности используется формула, которая основана на свойствах прямоугольных треугольников, образованных радиусом окружности, диаметром и сторонами квадрата. Понимание этой формулы позволяет эффективно рассчитывать диаметр и другие параметры вписанных фигур.
Как вычислить диаметр вписанной окружности?

Для определения диаметра вписанной окружности в квадрате можно воспользоваться следующей формулой:
Диаметр = сторона квадрата * √2
Чтобы посчитать диаметр, необходимо знать длину стороны квадрата. Умножьте эту длину на корень из 2 (приблизительное значение √2 примерно равно 1.414), чтобы получить диаметр вписанной окружности.
Например, если сторона квадрата равна 10 см, то диаметр вписанной окружности будет 10 * 1.414 ≈ 14.14 см.
Формула для расчета и примеры

Для определения диаметра вписанной в квадрат окружности необходимо воспользоваться следующей формулой:
Диаметр = сторона квадрата * √2
Где сторона квадрата - это длина стороны квадрата, в который вписана окружность.
Пример расчета: если длина стороны квадрата равна 10 см, то диаметр вписанной в него окружности будет:
Диаметр = 10 * √2 ≈ 14.14 см
Связь диаметра вписанной окружности с квадратом
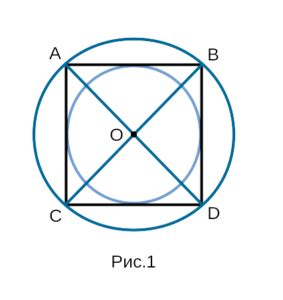
Геометрические характеристики
Для квадрата с вписанной в него окружностью с радиусом R можно выразить следующие геометрические характеристики:
- Диаметр вписанной окружности равен 2R.
- Сторона квадрата равна длине диаметра вписанной окружности, т.е. а = 2R.
- Площадь квадрата выражается формулой S = a^2 = (2R)^2 = 4R^2.
- Периметр квадрата равен P = 4a = 4 * 2R = 8R.
Значение диаметра вписанной окружности в математике
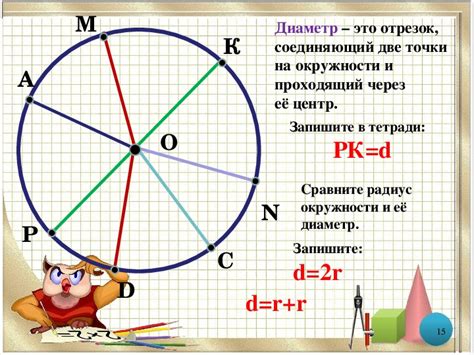
Знание диаметра вписанной окружности позволяет решать задачи, связанные с построением и характеристиками квадратов, а также определением различных геометрических параметров. Формула для расчета диаметра вписанной окружности в квадрате может быть использована для нахождения размеров фигур, а также для дальнейшего анализа и изучения геометрии.
Практическое применение

Знание диаметра вписанной в квадрат окружности имеет широкое применение в геометрии и инженерных расчетах. Например, при проектировании строений и сооружений, таких как колонны, башни или другие архитектурные элементы, зная диаметр вписанной окружности, можно точно определить размеры и форму объекта.
Также данное знание может быть полезно при расчетах в технике и машиностроении, где требуется точное определение геометрических параметров детали или механизма.
Поэтому понимание и умение использовать формулу для расчета диаметра вписанной в квадрат окружности поможет в применении математических знаний на практике и улучшит качество проектирования и расчетов.
Как использовать диаметр вписанной окружности в конструктивном проектировании?

Диаметр вписанной в квадрат окружности играет важную роль в строительном и конструктивном проектировании. Его значения можно использовать для определения размеров элементов конструкции, например, при создании несущих стен, колонн или других деталей.
Зная диаметр вписанной окружности, инженеры и архитекторы могут корректно определить расстояния между точками касания окружности и сторон квадрата, а также расположение элементов конструкции с учётом этих размеров.
Вопрос-ответ

Какая формула для вычисления диаметра вписанной в квадрат окружности?
Для вычисления диаметра вписанной в квадрат окружности используется формула: d = a*√2, где d - диаметр, а - сторона квадрата.
Как производится расчет диаметра вписанной в квадрат окружности?
Для расчета диаметра вписанной в квадрат окружности необходимо возвести длину стороны квадрата в квадрат, затем умножить полученный результат на корень из 2.
Зачем нужно знать диаметр вписанной в квадрат окружности?
Знание диаметра вписанной в квадрат окружности позволяет правильно расположить и вписать окружность внутрь квадрата, что может быть важно при решении геометрических задач и проектировании.



