Длина цепочки в информатике 3 – это один из ключевых понятий в теории алгоритмов. Она определяет количество вершин или элементов, через которые можно пройти от начальной точки до заданного элемента. В данной статье мы рассмотрим методы и алгоритмы для вычисления длины цепочки в информатике 3.
Понимание длины цепочки необходимо для эффективной работы с различными видами данных, структурами и задачами. Знание алгоритмов поиска и определения длины цепочки поможет вам разрабатывать более эффективные программы и решать сложные задачи в области информатики.
Алгоритм поиска длины цепочки х
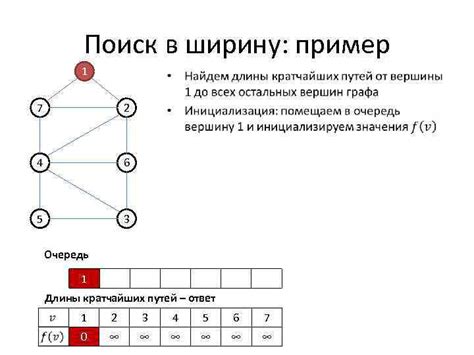
Для поиска длины цепочки x в информатике можно использовать следующий алгоритм:
| 1. | Инициализируем переменную для хранения длины цепочки. |
| 2. | Проходим по цепочке, увеличивая счетчик на каждом шаге. |
| 3. | После окончания прохода получаем длину цепочки. |
| 4. | Возвращаем полученное значение. |
Определение проблемы

Использование рекурсии для нахождения длины цепочки х

Для решения задачи нахождения длины цепочки х в информатике 3 можно использовать рекурсивный подход. Рекурсивная функция будет уменьшать задачу до более простых подзадач, пока не будет достигнуто базовое условие.
Пример реализации рекурсивной функции нахождения длины цепочки х:
| Код |
|---|
function длина_цепочки_x(х) { |
В данном примере функция длина_цепочки_x принимает аргумент x, проверяет базовый случай (если x пустая цепочка) и возвращает 0. В противном случае функция вызывает саму себя с уменьшенным аргументом (х.slice(1)) и увеличивает результат на 1.
Пример кода на языке Python
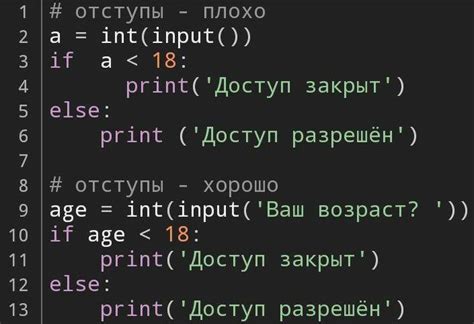
Ниже приведен пример кода на языке Python, который находит длину цепочки х:
def chain_length(x):
length = 1
while x != 1:
if x % 2 == 0:
x = x // 2
else:
x = 3 * x + 1
length += 1
return length
print(chain_length(7))
Анализ временной сложности

Для оценки эффективности алгоритма нахождения длины цепочки х в информатике 3 важно провести анализ его временной сложности. Временная сложность алгоритма определяет, сколько времени потребуется на его выполнение в зависимости от размера входных данных. Для анализа временной сложности можно использовать асимптотическую нотацию, такую как O-большое. Оценка временной сложности позволяет выбрать наиболее оптимальный алгоритм и оценить его производительность в различных условиях работы. Такой анализ поможет оптимизировать работу алгоритма и повысить его эффективность при решении задачи нахождения длины цепочки х в информатике 3.
Использование динамического программирования

Для нахождения длины цепочки х в информатике 3 можно применить метод динамического программирования. Этот метод позволяет эффективно решать задачи, разбивая их на подзадачи и запоминая результаты уже решенных подзадач. Таким образом, избегается повторное вычисление и увеличивается производительность алгоритма.
Для использования динамического программирования в нахождении длины цепочки х необходимо определить базовые случаи задачи, разработать рекурсивную формулу для вычисления оптимального решения и реализовать алгоритм, который будет эффективно запоминать результаты уже вычисленных подзадач.
Преимущества и недостатки методов

Однако у методов есть и недостатки. Например, большое количество методов может привести к избыточному использованию памяти, что может сказаться на производительности программы. Кроме того, сложные взаимосвязи между методами могут затруднить понимание кода и его отладку.
Вопрос-ответ

Как найти длину цепочки х в информатике?
В информатике длина цепочки x может быть найдена с помощью функции strlen() в большинстве программирования языков. Данная функция возвращает количество символов в строке x. Например, в языке Си можно использовать следующий код: int len = strlen(x);
Как добавить проверку на пустую строку перед нахождением длины цепочки x в информатике?
Прежде чем находить длину цепочки x, можно добавить проверку на пустую строку. Например, в языке программирования Си можно использовать условие if(strlen(x) == 0) для проверки. Если строка x пустая, программа может вывести сообщение об ошибке или выполнить соответствующие действия.
Могут ли возникнуть проблемы при вычислении длины цепочки x в информатике?
При вычислении длины цепочки x в информатике могут возникнуть проблемы, если строка содержит специальные символы, которые могут быть интерпретированы неправильно. Также необходимо учитывать возможные ошибки в коде, например, неправильная инициализация строки. Важно правильно обрабатывать исключения и ошибки для корректной работы программы.
Какие еще методы, помимо strlen(), можно использовать для определения длины строки x в информатике?
Помимо функции strlen(), можно использовать различные методы для определения длины строки x в информатике. Например, для некоторых языков программирования существуют встроенные методы или функции для работы со строками. Также можно использовать циклы для подсчета символов в строке. Кроме того, можно написать собственную функцию для определения длины строки, если требуется особая логика обработки.



