Что такое неравенство 4х?
Неравенство 4х – это математическое утверждение, которое сравнивает два числа или выражения и указывает на то, какое из них больше или меньше. Проверка неравенств – важный аспект алгебры, который помогает определить диапазон значений переменных и решать различные задачи.
В данной статье мы разберем, как эффективно проверять и решать неравенства, связанные с числом 4, и какие методы и приемы можно использовать для это
Проверка неравенства: 4х
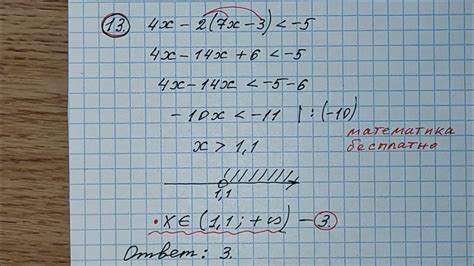
Для проверки неравенства 4х необходимо выполнить следующие шаги:
| 1. | Подставить значение переменной x в неравенство. |
| 2. | Умножить полученное значение переменной на 4. |
| 3. | Сравнить полученное значение с исходной переменной x. |
Если результат умножения переменной x на 4 больше исходного значения x, то неравенство 4х верно. В противном случае неравенство неверно.
Определение задачи проверки

1. Выразить переменную \(x\) из данного неравенства: \(x
2. Упростить выражение: \(x
Таким образом, задача проверки неравенства \(4x
Методы решения математических неравенств

1. Метод подстановки: При данном методе необходимо подставить различные значения переменной в неравенство и определить, при каких значениях неравенство будет верным.
2. Метод преобразования: Для решения неравенств часто используют метод преобразования, при котором проводят алгебраические действия с неравенством, чтобы получить простую форму и отыскать интервалы, при которых оно выполняется.
3. Графический метод: С помощью построения графика функции или неравенства на координатной плоскости можно определить интервалы значений переменной, при которых неравенство верно.
4. Использование тригонометрических и логарифмических неравенств: В случае, если в неравенстве присутствуют тригонометрические или логарифмические функции, следует применять соответствующие методы анализа и решения.
Использование графиков для наглядной проверки

Графики можно использовать для визуализации неравенства 4х < 12 и его проверки. Для этого нужно построить график функции y=4x и график функции y=12. Точка пересечения этих двух графиков будет точкой удовлетворяющей неравенству 4х < 12. Если точка пересечения находится слева от этой точки, то неравенство верно.
Используя графики, можно наглядно увидеть, какие значения x удовлетворяют неравенству, а какие нет. Такой подход позволяет с лёгкостью проверить и понять, какие числа x удовлетворяют данному неравенству, а какие нет.
Примеры решения неравенств с числами

Рассмотрим несколько примеров решения неравенств с числами:
- Решим неравенство: 4x
- Для начала разделим обе части неравенства на 4, получим: x
- Таким образом, все значения x, которые меньше 5, удовлетворяют данное неравенство.
Продолжение следует...
Разбор сложных случаев с дробями и корнями

При проверке неравенства с дробными коэффициентами и корнями важно быть внимательным к особенностям каждого случая. Например, при наличии дробей в неравенстве необходимо учитывать знаки числителя и знаменателя, чтобы правильно определить направление неравенства. Аналогично, при наличии корней необходимо анализировать их значения и возможные выражения под ними для правильного решения задачи. Такие сложные случаи требуют тщательного анализа и внимательности при выполнении проверки.
Полезные советы при работе с уравнениями

При решении уравнений важно следовать определенным шагам, чтобы избежать ошибок. Ниже приведены некоторые полезные советы:
| 1. | Внимательно читайте условие задачи и выделите все важные данные. |
| 2. | Применяйте соответствующие методы решения уравнений (например, методы подстановки или преобразования). |
| 3. | Проверяйте полученное решение, подставляя его обратно в уравнение и проверяя равенство обеих частей. |
| 4. | Обращайте внимание на знаки при выполнении арифметических операций, чтобы избежать ошибок. |
| 5. | Помните о свойствах математических операций (например, работа с дробями и степенями). |
Тесты для проверки навыков и знаний по неравенствам
Для проверки вашего понимания неравенств предлагаем выполнить следующие задания:
Задание 1:
Решите неравенство: 4x > 12. В ответе укажите диапазон значений x, при которых неравенство выполняется.
Задание 2:
Найдите все целочисленные значения x, для которых 4x - 5 < 3x + 7.
Задание 3:
Решите систему неравенств: 2x + 1 ≥ 5 и 3x - 2 < 7. Определите область значений x, удовлетворяющую обоим условиям.
Успехов в проверке ваших знаний по неравенствам!
| 1. | Внимательно изучить условия задачи и правильно интепретировать неравенство 4x. |
| 2. | Правильно подставлять значения переменной x и учитывать все возможные варианты. |
| 3. | Использовать алгебраические методы решения неравенств для нахождения верного ответа. |
| 4. | Проверять полученные результаты и убедиться в их корректности. |
Соблюдение этих рекомендаций поможет успешно решать задачи, связанные с неравенством 4x и улучшит навыки работы с математическими утверждениями.
Вопрос-ответ

Как проверить неравенство 4хЧтобы проверить неравенство 4хПочему неравенство 4хНеравенство 4хМожет ли неравенство 4хНет, неравенство 4хКакие значения переменной х удовлетворяют неравенству 4хЗначения переменной х, удовлетворяющие неравенству 4хКакое неравенство будет истинным при х = 5?
При х = 5, неравенство 4х
Почему неравенство 4хНеравенство 4хМожет ли неравенство 4хНет, неравенство 4хКакие значения переменной х удовлетворяют неравенству 4хЗначения переменной х, удовлетворяющие неравенству 4хКакое неравенство будет истинным при х = 5?
При х = 5, неравенство 4х
Может ли неравенство 4хНет, неравенство 4хКакие значения переменной х удовлетворяют неравенству 4хЗначения переменной х, удовлетворяющие неравенству 4хКакое неравенство будет истинным при х = 5?
При х = 5, неравенство 4х
Какие значения переменной х удовлетворяют неравенству 4хЗначения переменной х, удовлетворяющие неравенству 4хКакое неравенство будет истинным при х = 5?
При х = 5, неравенство 4х
Какое неравенство будет истинным при х = 5?
При х = 5, неравенство 4х



