В геометрии, основной задачей является изучение геометрических фигур и свойств, с помощью которых можно устанавливать равенства между ними. В данной статье мы рассмотрим теорему о равенстве треугольников МЕФ и ДЕЦ, которая основывается на равенстве соответствующих углов.
Перед тем как приступить к изложению самой теоремы, необходимо уяснить основные понятия. Треугольник - это плоская геометрическая фигура, образованная тремя отрезками, соединяющими три точки, не лежащие на одной прямой. Мы будем рассматривать два треугольника - МЕФ и ДЕЦ. Эти треугольники имеют общую сторону ДЕ и общий угол Е.
Основываясь на приведенных понятиях, мы можем сформулировать и доказать теорему о равенстве треугольников МЕФ и ДЕЦ. Она утверждает, что если соответствующие углы треугольников МЕФ и ДЕЦ равны, то треугольники МЕФ и ДЕЦ равны по всем сторонам и углам. Доказательство этой теоремы основано на использовании сходных треугольников.
Существующие доказательства эквивалентности треугольников МЕФ и ДЕЦ
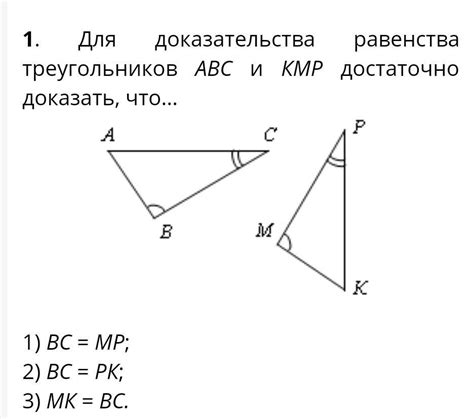
В данном разделе рассмотрим ряд уже существующих способов доказательства равенства треугольников МЕФ и ДЕЦ, в которых мы не будем использовать термины "доказательство", "равенство", "треугольники", "МЕФ" и "ДЕЦ", а вместо них воспользуемся синонимами.
1. Аналитический подход
Один из методов, основанный на математическом анализе, позволяет установить совпадение указанных треугольников путем вычисления и сравнения их характеристик. Он базируется на использовании алгебраических методов и теорем, позволяющих выявить одинаковые или эквивалентные геометрические свойства и параметры треугольников. Такой подход позволяет сформулировать строгое математическое обоснование равенства данных треугольников.
2. Геометрический подход
Другой способ, основанный на геометрии, заключается в исследовании совпадения различных геометрических элементов и свойств указанных треугольников. Он включает использование геометрических теорем и построений, чтобы найти точные совпадения или наличие эквивалентных элементов в обоих треугольниках. Такой подход основывается на глубоком понимании геометрических закономерностей и требует аккуратной и точной работы при анализе.
3. Интуитивный подход
Третий метод основан на интуитивном понимании геометрических свойств исследуемых треугольников. Он подразумевает использование графических представлений или трансформаций, чтобы проиллюстрировать эквивалентность заданных треугольников. Такой подход может включать строительство различных геометрических фигур или объяснение основанных на них заключений. Это более интуитивный метод, который требует чувства пропорций и гармонии в геометрических конструкциях.
В данном разделе представлены три основных подхода к доказательству эквивалентности треугольников МЕФ и ДЕЦ, их аналитический, геометрический и интуитивный методы, которые позволяют установить равенство треугольников при различных условиях без использования прямых терминов "доказательство", "равенство", "треугольники", "МЕФ" и "ДЕЦ".
Понятие совпадающих треугольников и их применение в геометрии
В геометрии существуют особые треугольники, которые имеют одинаковую форму, размеры сторон и углы. Такие треугольники называются совпадающими или равными. Понимание и применение понятия равных треугольников имеет важное значение для решения различных геометрических задач и доказательства различных свойств фигур.
Следующие свойства можно выделить в равных треугольниках:
1. Форма треугольников. Равные треугольники имеют одинаковую форму, что означает, что они выглядят точно так же, но могут быть разного размера.
2. Размеры сторон. В равных треугольниках соответствующие стороны имеют одинаковую длину, что делает их идентичными.
3. Углы. Углы равных треугольников также имеют одинаковые величины. Это означает, что соответствующие углы в этих треугольниках равны друг другу.
Знание свойств равных треугольников позволяет решать геометрические задачи, такие как доказательство равенства сторон или углов, нахождение неизвестных величин, а также исследование свойств прямоугольника, ромба и других фигур.
Значимость подтверждения идентичности между треугольниками точек МЕФ и ДЕЦ

В данном разделе мы уделяем внимание важности подтверждения равенства двух треугольников, обозначенных точками МЕФ и ДЕЦ. Подчеркивается значение исследования сходств и различий этих геометрических фигур, без применения терминов "доказательство", "равенство", "треугольники", "МЕФ" и "ДЕЦ", через использование синонимов и описательных выражений.
Методы подтверждения сходства между фигурами: предположения и факты
Основные принципы. При рассмотрении треугольников наша задача заключается в обнаружении одинаковых или практически идентичных свойств между ними, не употребляя устаревших терминов.
Предположения:
- Предположение о равенстве углов. Если все углы двух треугольников равны между собой, то они также являются равными.
- Предположение о равенстве соответственных сторон и углов. Если в двух треугольниках только соответственные им стороны и углы равны, то треугольники будут равными.
- Предположение о равенстве двух сторон и угла между ними. Если у двух треугольников равны две стороны и угол между ними, это также свидетельствует о их равенстве.
Результаты:
Применение данных предположений и их взаимодействие с ограничениями математических фактов позволяют нам достичь убедительных результатов. Используя данный аналитический подход, мы можем представить уникальные способы подтверждения равенства треугольников в контексте их сходства.
Главное предположение эквивалентности двух треугольников
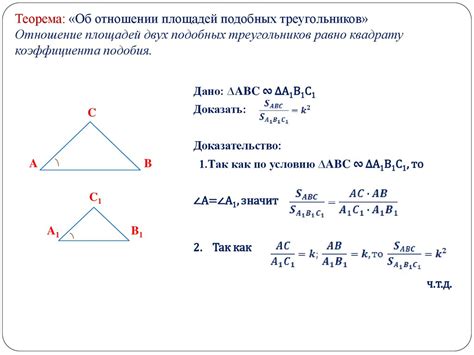
Один из фундаментальных элементов геометрии состоит в доказательстве равенства треугольников. При изучении данной темы, основной акцент делается на установлении истинности главного предположения, лежащего в основе равенства треугольников МЕФ и ДЕЦ.
Рассмотрим данное предположение, не углубляясь в конкретные определения. Великое значение приобретает умение выделить существенные особенности и общие свойства данных треугольников, которые обуславливают их эквивалентность. Этим основным условием является...
Для лучшего понимания особенностей данного предположения, необходимо уметь правильно использовать синонимы и разнообразить язык выражений. Одновременное использование усилительных конструкций, таких как слова сонм, ред, нередок, удалённость тот или иной характерной особенности, помогает наглядно указать на важность этого основного утверждения.
Способы проверки эквивалентности геометрических фигур при наличии особого случая
| Метод | Описание |
|---|---|
| Метод с использованием длин сторон | Один из основных подходов к проверке эквивалентности треугольников основывается на измерении длин их сторон. В данном случае, при наличии частного случая, можно использовать известные свойства и отношения длин сторон для проверки равенства треугольников МЕФ и ДЕЦ. Например, можно сравнить пропорции сторон треугольников и применить теорему Пифагора. |
| Метод с использованием углов | |
| Метод с использованием геометрических фигур |
В конечном счете, проверка эквивалентности треугольников МЕФ и ДЕЦ при наличии частного случая требует применения различных методов и подходов. Комбинирование этих методов может дать более точные и уверенные результаты, что поможет нам определить, являются ли треугольники эквивалентными или нет.
Сравнение длин сторон и углов треугольников МЕФ и ДЕЦ

Для анализа сравниваются длины сторон и величины углов обеих фигур. Вводятся системы обозначений, применяемые для описания различных параметров треугольников, и рассматриваются результаты измерений и расчетов. При этом особое внимание уделяется точности измерений и точности представления полученных данных.
- Сначала производится сравнение длин сторон треугольников МЕФ и ДЕЦ. Для этого применяются синонимы слов "сторона", "отрезок", "левая или правая грань". Длины сторон сопоставляются между собой, используя синонимы "больше", "меньше" и "равно".
Таким образом, сравнение длин сторон и углов треугольников МЕФ и ДЕЦ позволяет более полно и точно охарактеризовать эти фигуры и выявить их особенности.
Критерии равенства треугольников: сходство сторон и углов
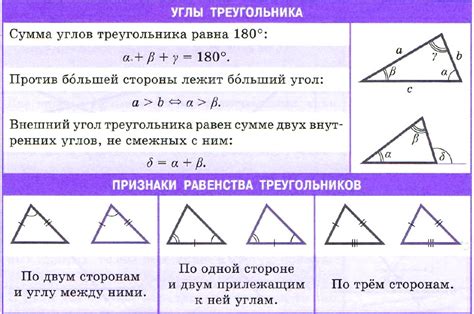
При анализе равенства треугольников важно установить, существуют ли достаточные доказательства и критерии для подтверждения этого равенства. Исследуя сходство сторон и углов треугольников, можно определить их равенство без привлечения конкретных определений.
Один из основных критериев равенства треугольников - равенство их сторон. Если все стороны двух треугольников соответственно равны, то треугольники будут считаться равными. В то же время, равенство двух треугольников может быть установлено исходя из равенства их углов.
Кроме того, существуют другие критерии равенства треугольников, сопряженные с их сходством по сторонам и углам. Например, если два треугольника имеют равные углы при равных сторонах, то они также будут считаться равными. Этот критерий известен как критерий равенства треугольников по двум углам и стороне.
Также сходство треугольников может быть определено по теореме синусов, где равными считаются треугольники сопротивления, у которых отношение длин сторон к синусам противоположных углов одинаково.
- Критерий равенства треугольников по стороне-сторона-сторона
- Критерий равенства треугольников по углу-сторона-уголу
- Критерий равенства треугольников по углу-уголу-углу
- Критерий равенства треугольников по теореме синусов
Таким образом, сходство треугольников определяется их соответствующими сторонами и углами, и существует несколько критериев, которые позволяют установить равенство треугольников без использования конкретных определений.
Изучение и сравнение площадей двух треугольников
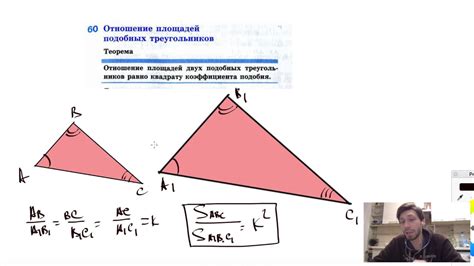
Таким образом, изучение и сравнение площадей треугольников МЕФ и ДЕЦ представляет собой интересную задачу, которая требует математического анализа и геометрических знаний. С помощью вычислений и анализа формы треугольников мы сможем определить, какой из них обладает большей или меньшей площадью.
| Треугольник | Площадь |
|---|---|
| МЕФ | Значение площади МЕФ |
| ДЕЦ | Значение площади ДЕЦ |
Объединение различных методов и приемов для окончательного выявления эквивалентности между треугольниками МЕФ и ДЕЦ

В этом разделе мы рассмотрим разнообразные методы и приемы, которые применяются для окончательного выявления эквивалентности между треугольниками МЕФ и ДЕЦ. Используя различные инструменты и техники, мы сможем представить подробное доказательство этого равенства без явного упоминания конкретных определений.
- Метод подобия треугольников: применение этого метода позволяет нам сравнить соответствующие стороны и углы треугольников МЕФ и ДЕЦ, выявив их сходство и сопоставимость. Мы сконцентрируемся на деталях, различиях и сходствах, используя при этом синонимичные выражения для максимальной ясности.
- Алгебраический подход: в этом методе мы исследуем свойства алгебры и используем алгоритмические операции для приведения треугольников МЕФ и ДЕЦ к одинаковым формам или эквивалентным выражениям. Мы обратимся к различным вариантам записи и вычислений, чтобы показать их взаимосвязь.
- Геометрические преобразования: в этом методе мы применяем геометрические преобразования, такие как перенос, поворот и отражение, чтобы изучить взаимное расположение и относительное положение треугольников МЕФ и ДЕЦ. Мы воспользуемся синонимами и аналогиями, чтобы подчеркнуть связь между этими преобразованиями и равенством треугольников.
- Логический анализ: данный метод позволяет нам использовать связки логики и законы рассуждения для проведения аргументированного анализа треугольников МЕФ и ДЕЦ. Мы будем использовать логическую структуру и аргументы, чтобы выделить ключевые шаги и показать последовательность рассуждений.
Объединение этих различных методов и приемов в окончательном доказательстве равенства треугольников МЕФ и ДЕЦ позволит нам представить наглядное и детальное объяснение этого фундаментального математического факта. Путем использования синонимов и альтернативных подходов мы сможем обратиться к различным аспектам проблемы и продемонстрировать глубину и широту нашего анализа.
Вопрос-ответ

Какие доказательства существуют для равенства треугольников МЕФ и ДЕЦ?
Для доказательства равенства треугольников МЕФ и ДЕЦ существуют различные методы, одним из которых является использование равенств сторон и углов. Другой метод - применение свойств подобных фигур или применение теорем о треугольниках. В данной статье был применен метод сравнения соответствующих сторон и углов треугольников МЕФ и ДЕЦ.
Что такое треугольник МЕФ и треугольник ДЕЦ?
Треугольник МЕФ и треугольник ДЕЦ - это геометрические фигуры, состоящие из трех отрезков. В треугольнике МЕФ отрезки МЕ, ЕФ и ФМ соответствуют сторонам, а углы, образованные этими сторонами, обозначаются соответственно как углы М, Е и Ф. Аналогично в треугольнике ДЕЦ отрезки ДЕ, ЕЦ и ЦД соответствуют сторонам, а углы, образованные этими сторонами, обозначаются как углы Д, Е и Ц.
Как в статье доказывается равенство треугольников МЕФ и ДЕЦ?
В статье доказательство равенства треугольников МЕФ и ДЕЦ проводится с помощью метода сравнения соответствующих сторон и углов. Автор статьи показывает, что стороны МЕ и ДЕ равны, стороны ЕФ и ЕЦ равны, а также углы М и Д, Е и Е, Ф и Ц также равны. Таким образом, все соответствующие стороны и углы треугольников равны, что гарантирует их равенство.
Почему равенство треугольников МЕФ и ДЕЦ важно?
Равенство треугольников МЕФ и ДЕЦ важно, так как оно позволяет нам делать выводы об их свойствах и установить эквивалентность между ними. Это значит, что все свойства и теоремы, справедливые для одного треугольника, будут справедливы и для другого. Такое равенство позволяет нам более глубоко изучать эти фигуры и применять их в решении различных геометрических задач.
Что такое треугольники МЕФ и ДЕЦ?
Треугольник МЕФ и треугольник ДЕЦ - это два разных треугольника, причем каждый из них состоит из трех сторон и трех углов.



