Когда мы имеем дело с геометрией, существует множество методов, которые помогают нам решить различные задачи. Одной из таких задач является вычисление площади сегмента окружности, зная длину ее диаметра.
Это может быть полезно, когда нам необходимо рассчитать площадь определенной области, ограниченной дугой окружности и ее хордой. Для выполнения этой задачи нам необходимо знать не только длину диаметра, но и другие параметры, такие как радиус и центр окружности.
Используя формулы и теоремы геометрии, мы можем найти оставшиеся параметры и вычислить площадь сегмента окружности. Для более точных результатов, рекомендуется использовать точные значения чисел и строго следовать математическим операциям.
Основные понятия и определения

В данном разделе рассмотрим фундаментальные понятия и определения, связанные с нахождением части окружности при известном диаметре. Познакомимся с основными терминами, которые помогут нам лучше понять и решить поставленную задачу.
Диаметр - это отрезок, соединяющий две точки на окружности и проходящий через ее центр. В данном случае, когда мы знаем диаметр, это поможет нам определить размеры и форму окружности.
Окружность - это фигура, состоящая из всех точек на плоскости, которые равноудалены от одной фиксированной точки, называемой центром окружности. Окружность является одним из важнейших геометрических объектов и широко используется в различных областях науки и инженерии.
Часть окружности - это участок окружности, ограниченный двумя точками на окружности или дугой, которая может быть любой частью окружности, от меньшей доли, до половины или даже большего фрагмента.
Сектор окружности - это часть окружности, ограниченная двумя радиусами и дугой между ними. Сектор окружности может измеряться в градусах или радианах и отражает угловую величину этого сектора.
Дуга окружности - это участок окружности между двумя точками. Дуга окружности может иметь различную длину в зависимости от своего положения на окружности и угла, создаваемого этой дугой.
Знание и понимание этих основных терминов является важным шагом для решения задачи по нахождению части окружности при известном диаметре. Теперь, когда мы уяснили основные понятия и определения, перейдем к более конкретным методам и подходам к решению поставленной задачи.
Известная формула для вычисления периметра окружности

Для вычисления длины окружности используется формула, основанная на соотношении между радиусом и длиной окружности. Радиус - это расстояние от центра окружности до любой ее точки, а диаметр - это расстояние между двумя диаметрально противоположными точками на окружности.
Известная формула для вычисления длины окружности: L = πd
Где L - длина окружности, d - диаметр окружности, а π (пи) - математическая константа, равная примерно 3.14159. Пи является бесконечной и иррациональной десятичной дробью и используется для приближенного вычисления периметра окружности.
| Диаметр окружности (d) | Длина окружности (L) |
|---|---|
| 1 | 3.14 |
| 2 | 6.28 |
| 3 | 9.42 |
| 4 | 12.57 |
Таблица выше показывает примеры вычисления длины окружности для различных значений диаметра. Можно заметить, что с увеличением диаметра, длина окружности также увеличивается, пропорционально умножаясь на значение пи.
Расчет части окружности с заданным диаметром
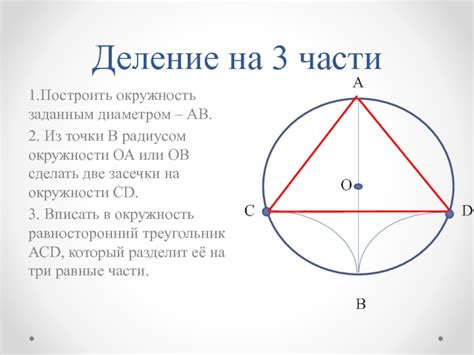
- Определите значение диаметра для заданной окружности. Диаметр - это отрезок, соединяющий две точки на окружности и проходящий через ее центр. Обычно он обозначается символом "d".
- Вычислите радиус окружности по известному значению диаметра. Радиус - это половина диаметра и обозначается символом "r". Формула для вычисления радиуса: r = d / 2.
- Выберите значение угла, определяющего часть окружности, которую вы хотите найти. Обычно угол измеряется в градусах и обозначается символом "θ".
- Примените формулу для расчета длины дуги окружности с заданным радиусом и углом. Формула: длина дуги = (θ/360) * 2πr.
Таким образом, зная диаметр окружности, мы можем вычислить радиус и, затем, с помощью формулы длины дуги окружности, найти нужную нам часть окружности.
Угол сектора окружности: определение и свойства

Угол сектора окружности определяется как угол между двумя лучами, исходящими из центра окружности и ограничивающими дугу данного сектора. Он измеряется в радианах или градусах и обозначается символом α. По своей природе угол сектора окружности является центральным углом, описывающим дугу сектора и соединяющим точки, лежащие на окружности.
Угол сектора окружности имеет ряд важных свойств. Во-первых, его величина пропорциональна длине дуги сектора. То есть, при изменении длины дуги, угол сектора также изменяется, сохраняя пропорциональность. Во-вторых, сумма углов секторов окружности, имеющих общую вершину и лежащих на одной окружности, равна 360 градусам или 2π радианам.
Для вычисления величины угла сектора окружности можно использовать различные методы, такие как применение тригонометрических функций или использование геометрических формул. Применение соответствующих формул позволяет не только определить угол сектора, но и провести его построение на плоскости.
| Свойства угла сектора окружности: |
|---|
| Пропорциональность угла и дуги сектора |
| Сумма углов секторов на окружности |
| Методы вычисления угла сектора |
Формула для расчета дуги окружности
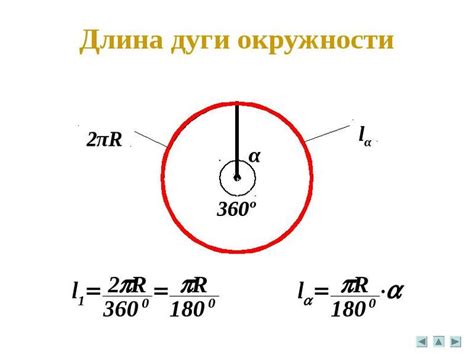
В данном разделе мы рассмотрим способ вычисления длины дуги окружности, используя известные параметры исходной фигуры. Необходимо определить меру дуги окружности, однако при этом избегая характерных терминов, описывающих процесс нахождения части окружности.
Для вычисления длины сектора окружности вам потребуется знать его радиус и центральный угол, который соответствует данному сектору. Используя формулу для длины дуги окружности, можно рассчитать ее значение с помощью математических операций и заданных параметров. Полученный результат представляет собой меру длины сектора окружности.
- Для вычисления длины сектора окружности необходимо выполнить следующие шаги:
- Определите радиус окружности, который является половиной диаметра.
- Определите центральный угол, который соответствует сектору окружности.
- Установите соответствующие значения радиуса и центрального угла в формулу для длины дуги окружности.
- Выполните необходимые математические операции для получения меры длины сектора окружности.
- Полученный результат будет являться искомой величиной - длиной сектора окружности.
Таким образом, зная радиус и центральный угол сектора окружности, вы можете использовать формулу для расчета его длины. Этот метод позволяет определить меру дуги окружности без использования терминов и понятий, связанных с нахождением части окружности при известном диаметре.
Примеры вычислений

В этом разделе мы рассмотрим примеры расчетов, связанных со свойствами геометрической фигуры, которую мы называем "окружностью".
- Пример 1: Расчет площади полукруга
- Шаг 1: Найдите радиус окружности, используя известный диаметр и формулу радиуса окружности.
- Шаг 2: Вычислите площадь полукруга, используя найденный радиус и формулу площади полукруга.
- Пример 2: Расчет длины дуги окружности
- Шаг 1: Найдите радиус окружности, используя известный диаметр и формулу радиуса окружности.
- Шаг 2: Вычислите длину окружности, используя найденный радиус и формулу длины окружности.
- Шаг 3: Получите длину дуги окружности, зная процент от всей окружности и соответствующую формулу.
Это лишь некоторые из примеров вычислений, которые могут быть полезны при работе с частями окружности. Запомните, что вычисления в геометрии важны для понимания и применения математических концепций в реальных задачах. Используйте эти примеры, чтобы упражняться в своих навыках и лучше понять, как работать с окружностями.
Пример 1: Определение длины доли окружности с известным углом
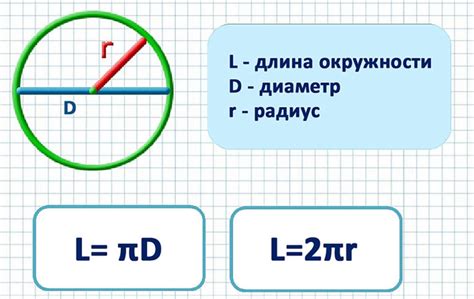
В данном примере мы рассмотрим способ определения длины части окружности с помощью известного угла. Зная значение угла и диаметр окружности, мы сможем вычислить длину сектора.
Давайте представим, что у нас есть окружность с известным диаметром. Чтобы найти длину сектора, нам необходимо знать еще один параметр - угол, который сформирован дугой, ограниченной этими двумя радиусами окружности.
Угол может быть выражен в различных единицах измерения, например, в градусах, радианах или градах. Независимо от единицы измерения, принцип определения длины сектора остается прежним.
Для нахождения длины сектора с известным углом воспользуемся формулой: длина сектора = (длина окружности * угол) / 360.
Здесь длина окружности определяется по формуле: длина окружности = π * диаметр, где π - математическая константа, примерно равная 3.14159.
Используя данную формулу, мы сможем легко определить длину сектора окружности с известным углом и диаметром.
Пример 2: Определение меры угла сектора при заданной длине

В процессе изучения окружностей важно уметь определить меру угла сектора на основе его известной длины. Знание этого позволяет более точно анализировать геометрические свойства окружностей и эффективно решать задачи, связанные с построением и измерениями.
Для нахождения меры угла сектора, когда известна его длина, можно применить определенные формулы, основанные на связи между данной длиной, радиусом и длиной окружности.
В данном примере рассмотрим методику вычисления меры угла сектора при известной длине. Приведенная формула позволит эффективно решать задачи, связанные с определением меры угловых участков окружности на основе конкретных цифр и без необходимости использования инструментов измерения.
Помимо формулы, для определения меры угла сектора потребуется использование понятия радианы – угловой единицы, соответствующей дуге, длина которой равна радиусу окружности. Зная соотношение между радианами и градусами, можно трансформировать полученное значение в удобную для рассмотрения меру измерения.
Таким образом, при наличии информации о длине сектора окружности можно определить меру угла, который он занимает на окружности. Это позволяет решать различные геометрические задачи и проводить точные измерения без использования сложных инструментальных средств.
Практическая применимость

Начнем с того, что наша задача состоит в том, чтобы определить, каким образом можно использовать знания о диаметре окружности для вычисления ее части. Это знание имеет практическую ценность в различных областях, где требуется расчет и проектирование объектов, зависящих от геометрических параметров окружности.
Один из наиболее распространенных случаев применения этого знания - в строительстве. Например, при проектировании и строительстве арок, дуг и куполов диаметр окружности является важным параметром, который определяет размеры и форму конструкции. Зная диаметр, можно рассчитать угол дуги, а также определить размеры и радиусы других элементов конструкции.
Еще одним практическим применением этого знания является машиностроение. Например, в технике точения на токарных станках при обработке деталей с окружностной формой знание диаметра окружности позволяет определить размеры и углы резцов, а также выбрать оптимальную стратегию обработки для достижения требуемой точности и геометрии детали.
| Практические области применения | Примеры |
|---|---|
| Строительство | Проектирование арок, дуг, куполов |
| Машиностроение | Точение на токарных станках |
Важные аспекты для учета в задачах о нахождении долей окружности

Моменты, которые нужно учесть
При рассмотрении задач, связанных с определением долей окружности, существуют несколько важных аспектов, которые следует учитывать. В первую очередь, необходимо понимать, что окружность - это геометрическая фигура, ограниченная кривой линией. При рассмотрении ее части, являющейся сегментом, требуется учитывать диаметр - основной параметр, определяющий размер и форму сегмента.
Аспекты, связанные с радиусом
Для правильного определения доли окружности необходимо учитывать значение диаметра, который становится осью симметрии всей окружности. Используя диаметр, можно легко определить радиус. Радиус - это расстояние от центра до любой точки на окружности. Зная радиус, можно определить угол в радианах, который соответствует искомой доле окружности. Угол зависит от периметра сегмента и отношения его к длине окружности.
Различные сегменты окружности
Сегмент окружности может представлять собой различные части фигуры, определяемые углами или длиной дуги. От выбора конкретного сегмента будут зависеть методы решения задачи и используемые формулы. Кроме того, следует учитывать, что окружность может разделяться не только на сегменты, но и на секторы и дуги. Каждый из этих видов фигур имеет свои характеристики и формулы для определения их параметров.
Дополнительные факторы
Помимо диаметра и радиуса, при определении долей окружности следует учесть также угол наклона и значение площади сегмента. Угол наклона определяет положение сегмента относительно центра окружности, и может использоваться для определения доли окружности в процентах или градусах. Площадь сегмента является мерой его площади, и может быть рассчитана с использованием соответствующих формул, учитывающих радиус и угол сегмента.
Вопрос-ответ

Как найти площадь части окружности при известном диаметре и угле?
Для того чтобы найти площадь части окружности при известном диаметре и угле, нужно воспользоваться формулой: S = (π * r^2 * α) / 360, где S - площадь части окружности, r - радиус окружности (равный половине диаметра), α - угол, под которым соответствующая дуга протяженностью радиуса отклоняется от положения касательной.
Как найти длину дуги окружности при известном диаметре и угле?
Длина дуги окружности при известном диаметре и угле вычисляется по формуле: L = (π * D * α) / 360, где L - длина дуги окружности, D - диаметр окружности (расстояние между двумя точками на окружности, проходящими через ее центр), α - угол в градусах, описываемый данной дугой.
Можно ли найти площадь части окружности без знания угла?
Да, можно найти площадь части окружности без знания угла, если известна длина дуги данной части окружности. Для этого используется формула: S = (L * r) / 2, где S - площадь части окружности, L - длина дуги, r - радиус окружности.
Как найти длину дуги окружности при известной площади части окружности?
Для того чтобы найти длину дуги окружности при известной площади части окружности, нужно воспользоваться формулой: L = (√(S * 2 * r)) * 2, где L - длина дуги окружности, S - площадь части окружности, r - радиус окружности.



