Математика - это невероятно увлекательная наука, способная раскрыть перед нами тайны и закономерности нашего мира. Умение выполнять различные математические операции не только развивает наше логическое мышление, но и помогает в решении практических задач в повседневной жизни.
Каждая операция имеет свою уникальную суть, и сегодня мы поговорим о таком интересном случае в вычитании, когда разность вычитается из уменьшаемого. Этот вид задач требует особого подхода и позволяет нам глубже понять принципы вычитания.
К сожалению, часто стандартные математические задачи не могут полностью охватить исследуемую тему, потому что они предлагают нам примеры с конкретными числами и ситуациями. Однако, для полного понимания этого вида вычитания, нам необходимо уяснить суть задачи и научиться применять общую формулу для решения подобных примеров.
Основное правило для вычитания одного числа из другого
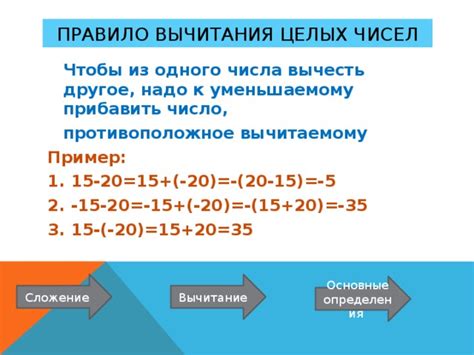
Для выполнения операции вычитания, направленной на получение разности двух чисел, существует основная формула. Это простое правило позволяет получить новое значение, вычитая разность из уменьшаемого числа.
Таким образом, в результате применения основной формулы, уменьшаемое число уменьшается на разность, а полученная разность становится новым значением.
Например:
- Уменьшаемое число: 10
- Разность: 3
- Применение формулы: 10 - 3 = 7
- Новое значение: 7
Также важно отметить, что применение данной формулы возможно только при наличии достаточного количества чисел для вычисления разности. Если разность или уменьшаемое неизвестны, необходимо использовать другие математические методы для нахождения этих величин.
Запись вычитания с использованием разности

В этом разделе мы рассмотрим, как правильно записать операцию вычитания, используя понятие разности.
Вычитание с разностью - это математическая операция, при которой уменьшаемое уменьшается на величину разности. Эта операция представляет собой процесс уменьшения числа на определенное значение, которое называется разностью. Запись вычитания с разностью позволяет более ясно и точно обозначить каждый элемент операции и получить итоговый результат.
- Для записи вычитания с разностью мы используем следующую формулу: уменьшаемое - разность = уменьшаемое с учетом вычитания;
- Уменьшаемое - это число, которое мы собираемся уменьшить;
- Разность - это значение, на которое мы уменьшаем уменьшаемое;
- Уменьшаемое с учетом вычитания - это число, полученное в результате операции вычитания.
Давайте рассмотрим пример, чтобы более наглядно представить, как записать вычитание с использованием разности.
- Уменьшаемое: 15;
- Разность: 7;
- Уменьшаемое с учетом вычитания: 15 - 7 = 8.
Таким образом, мы получаем, что 15 минус 7 равно 8. Запись вычитания с разностью позволяет ясно указать каждую составляющую операции и предоставляет возможность более точного представления процесса вычитания.
Как использование вычитания с разностью может быть полезным

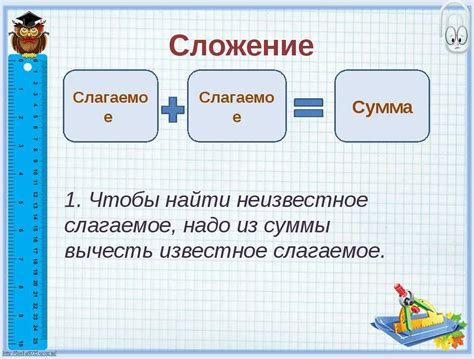
Когда мы вычитаем разность из уменьшаемого, мы производим обратную операцию к сложению. Это позволяет нам найти значение, которое необходимо вычесть из начального числа, чтобы получить конечный результат. Использование вычитания с разностью подходит для решения задач, где необходимо находить разность между двумя значениями или уменьшать значения по определенному шаблону.
Вычитание с разностью позволяет нам увидеть тенденции и зависимости между числами. Мы можем обнаружить, что разность между значениями увеличивается или уменьшается с каждым последующим шагом. Это может указывать на наличие закономерности или позволить предсказать будущий результат на основе имеющихся данных.
Кроме того, вычитание с разностью может быть полезным при анализе временных рядов или других последовательностей данных. Этот метод помогает выявить тренды и цикличность в данных, а также определить точки изменения и экстремумы. Таким образом, мы можем получить более полное представление о поведении и изменениях в данных.
Использование вычитания с разностью может быть полезным для различных областей знаний, включая математику, экономику, физику и программируемые науки. Этот метод позволяет нам более глубоко анализировать данные и получать более точные результаты. Благодаря его простоте и эффективности, вычитание с разностью остается одним из важных инструментов для решения задач в различных областях.
Применение вычитания с учетом разности в математике

Применение вычитания с разностью может быть полезно для определения изменений, установления связей между различными величинами, анализа трендов и многое другое. Эта операция позволяет оценить величину изменения по сравнению с исходным значением и получить информацию о направлении и интенсивности изменений.
Примером использования вычитания с разностью может быть анализ финансовых показателей компании. Путем вычитания текущих финансовых результатов относительно предыдущих можно определить, улучшилась ли ее финансовая ситуация или ухудшилась. Также, вычитание с разностью может применяться для определения изменения величины какого-либо показателя на процентном уровне, что может быть полезно при анализе статистических данных или трендов в различных областях.
Методика решения задач с вычитанием разности
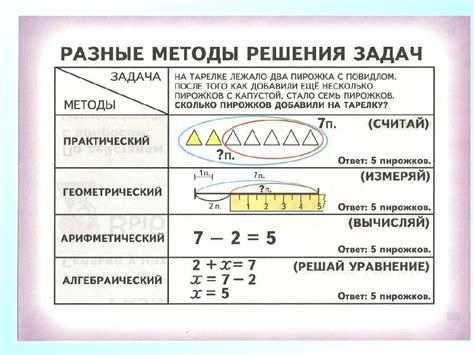
В данном разделе мы рассмотрим эффективный подход к решению задач, в которых требуется выполнить вычитание разности. Приведенные ниже методы их применения помогут вам легко и точно решать такие задачи.
Метод последовательного действия
Для начала, следует сконцентрироваться на том, какую информацию предоставляется для рабочих величин. Изначально стоит определить уменьшаемое значение, которое в дальнейшем будет вычитаться из разности. Затем, следует изучить приведенную разность, и на ее основе определить уменьшительное значение.
- Проанализируйте задачу на наличие значений уменьшаемого и разности. Установите, какие значения известны, а какие следует найти.
- Используйте известные значения для вычисления уменьшаемого: вычитайте разность из известного значения.
- Определите значение уменьшительного, вычитая полученный результат из известного уменьшаемого значения.
- Итоговый результат будет вычислен путем вычитания уменьшительного из уменьшаемого значения.
Метод решения с использованием примеров
Рассмотрим также простой способ решения задач с вычитанием разности, основанный на использовании примеров. Данная методика может быть особенно полезна для визуализации и эффективного понимания процесса решения.
- Сформулируйте задачу ясно и четко, опишите известные значения и то, что требуется найти.
- Выберите подходящий численный пример с конкретными значениями уменьшаемого и разности.
- Выполните вычитание разности из уменьшаемого и определите уменьшительное.
- Подставьте полученные значения в условие задачи и убедитесь, что они удовлетворяют поставленным условиям.
- Проведите проверку путем выполнения обратной операции - сложения уменьшаемого и уменьшительного. Результат должен совпадать с исходным изначальным уменьшаемым.
Выберите подход, наиболее удобный для вас, и с помощью указанных методов вы сможете успешно решать задачи, связанные с вычитанием разности. Практика и освоение этих методик помогут вам стать уверенным и эффективным в выполнении таких операций.
Особенности вычета с указанной разницей в учебниках

В учебниках математики обычно представлены различные случаи использования указанной разницы. Например, дается задание вычесть из числа его разность с другим числом. Это позволяет учащимся развить навык анализировать условие задачи и применять соответствующие действия. Возможны ситуации, когда указанная разность участвует не только в одном вычитании, но и в нескольких шагах, что добавляет дополнительную сложность и требует рассмотрения разных вариантов подхода к решению.
Особенность вычитания с указанной разностью приводит к тому, что учебники математики обычно содержат дополнительные примеры и задания для тренировки навыков работы с такими выражениями. Такие задания помогают учащимся улучшить навык применения соответствующей формулы и оценки результатов. Это также способствует развитию аналитического мышления и логического рассуждения.
Раскрытие специфики вычитания с указанной разностью в учебных материалах позволяет учащимся более полно изучить эту операцию, а также применять ее при решении конкретных задач. Последовательное усвоение этих особенностей поможет достичь более глубокого понимания математических концепций и повысить общую успеваемость в этой области знаний.
Ошибки, которые часто возникают при операции вычитания с числами, имеющими разность

При выполнении вычитания с числами, имеющими разность, существуют определенные ошибки, которые встречаются довольно часто. Избежать этих ошибок поможет понимание основных принципов вычитания и аккуратность при выполнении операции.
Одной из распространенных ошибок является неправильное понимание понятия разности. Некоторые люди путают понятие разности с понятием уменьшаемого или уменьшаемой разности. Это может привести к неправильному расчету и получению неверного результата.
Другой частой ошибкой является неправильный подход к выполнению операции вычитания. Некоторые люди пренебрегают правилами вычитания и производят некорректные вычисления, что приводит к неправильному результату. Необходимо помнить о важности правильного расположения чисел в задаче вычитания и последовательности шагов операции.
Также, стоит отметить ошибку, связанную с неправильным переносом при вычитании. Часто люди не осознают необходимость переноса при выполнении операции и пропускают этот шаг, что приводит к неправильному результату. Важно учитывать правила переноса и выполнять их на каждом шаге операции вычитания.
Наконец, пренебрежение знаками вычитания и их правильным использованием может также стать причиной ошибок при операции. Неверное определение знаков и их применение может значительно исказить результаты вычитания. Поэтому необходимо тщательно анализировать представленные знаки и их влияние на операцию.
Как применить операцию вычитания с разностью в повседневной жизни
- Управление бюджетом: Если вы хотите знать, сколько денег у вас останется после покупки определенного товара, операция вычитания с разностью может помочь вам. Вычитая стоимость товара из общего бюджета, вы сможете рассчитать, сколько останется денег на другие покупки.
- Планирование времени: Если вам нужно организовать свой день или неделю, операция вычитания с разностью может быть полезна для расчета доступного времени на различные задачи. Вычитая время, затраченное на одну задачу, из общего доступного времени, вы сможете оптимизировать расписание и установить приоритеты.
- Расчет остатка: Вычитание с разностью может применяться для расчета остатка или изменения величины. Например, если у вас есть определенное количество еды или напитков, вы можете вычесть использованное количество, чтобы узнать, сколько осталось.
- Управление ресурсами: Операция вычитания с разностью может быть полезна при управлении различными типами ресурсов, такими как топливо, энергия или материалы. Вычитая использованный объем из общего запаса, вы сможете контролировать и планировать использование ресурсов.
Дополнительные правила для более сложных ситуаций при вычитании с оставшимся

Одним из таких дополнительных правил является принцип переноса единицы. Если при вычитании из цифры уменьшаемого больше цифры разности, то из следующего разряда нужно "занять" единицу и прибавить ее к разности. Данный принцип позволяет правильно обрабатывать ситуации, когда нужно производить вычитание с переносом.
Еще одним правилом, применяемым в более сложных случаях вычитания, является использование разрядов с разными значениями. Большие разряды имеют большее значения, а меньшие - меньшее. При вычитании необходимо учитывать указанное значение разряда и использовать его для определения итогового результата.
Также в некоторых случаях может возникнуть необходимость использовать дополнительное округление для получения более точного значения разности. Это особенно важно при выполнении математических операций с большим количеством разрядов и точностью до определенного знака.
| Пример | Описание |
|---|---|
| 1234 - 456 | Используется принцип переноса единицы, так как из цифры 4 невозможно вычесть 6. Единица переносится из разряда справа, что приводит к увеличению разряда для вычитания до 14. Таким образом, итоговая разность составляет 778. |
| 5432 - 1091 | Используется разрядная система, при которой значения разрядов учитываются. Например, при вычитании цифры 1 из цифры 9, разряд со значением 10 позволяет получить результат 9-1=8. Таким образом, итоговая разность составляет 4341. |
| 9876 - 4321 | Дополнительное округление применяется для увеличения точности вычислений. В данном случае, округление до тысячных дает более точный результат, и итоговая разность составляет 5555. |
Возможности тренировки навыков вычитания с по-разному составленными задачами

Для разнообразия процесса обучения вычитанию, можно использовать различные вариации задач, которые позволят тренировать навыки вычитания с разностью в уменьшаемом. Это поможет учащимся более глубоко понять и усвоить математические концепции, а также развить логическое мышление и аналитические способности.
Одна из возможных вариаций задач на вычитание с разностью - это использование действительных ситуаций, в которых учащиеся должны применить вычитание для решения задач. Например, можно предложить задачу про сбор урожая на ферме, где ученики должны вычесть разницу числа собранных яблок из исходного количества яблок на дереве.
Еще одним подходом может быть использование графических изображений, которые помогут визуальному представлению задачи. Например, можно предоставить диаграмму, на которой изображены две группы предметов, а ученикам нужно вычесть разницу между ними, чтобы определить количество предметов в одной из групп.
Дополнительным методом тренировки может быть использование числовых последовательностей, в которых каждое следующее число получается путем вычитания разности из предыдущего числа. Это поможет учащимся понять связь между числами и вычислением разности в процессе вычитания.
Таким образом, использование разнообразных вариаций задач на вычитание с разностью позволяет эффективно тренировать навыки вычитания, развивать критическое мышление и визуальное восприятие, а также делает процесс обучения более интересным и увлекательным для учащихся.
Вопрос-ответ

Какая формула используется для вычитания разности из уменьшаемого?
Формула для вычитания разности из уменьшаемого выглядит следующим образом: уменьшаемое - разность = уменьшаемое.
Можете привести примеры использования вычитания разности из уменьшаемого?
Конечно! Пример №1: уменьшаемое 10, разность 5. Вычитаем разность из уменьшаемого: 10 - 5 = 5. Пример №2: уменьшаемое 20, разность 10. Вычитаем разность из уменьшаемого: 20 - 10 = 10.
Можно ли использовать формулу вычитания разности из уменьшаемого для любых чисел?
Да, формула вычитания разности из уменьшаемого применима для любых чисел. Вычитание разности из уменьшаемого можно выполнять как с положительными, так и с отрицательными числами.
Как происходит вычитание разности из уменьшаемого если уменьшаемое и разность равны?
Если уменьшаемое и разность равны, то результатом вычитания будет всегда ноль. Например, если уменьшаемое равно 8, а разность также равна 8, то 8 - 8 = 0.



