Коэффициент с в квадратном уравнении ax^2 + bx + c является коэффициентом при члене x. Он определяет величину второй степени в уравнении и влияет на форму графика параболы, которая является графиком квадратного уравнения. Коэффициент с влияет на положение вершины параболы и направление её открывания.
Изменение значения коэффициента с приводит к смещению параболы вверх или вниз по вертикали. Положительное значение с смещает параболу вверх, отрицательное – вниз. Коэффициент с также определяет точку пересечения параболы с осью ординат (ось y).
Роль коэффициента a в уравнении квадратного трехчлена

Коэффициент a в уравнении квадратного трехчлена ax^2 + bx + c играет важную роль, определяя форму параболы, которая представляет движение квадратного трехчлена на координатной плоскости.
Знак коэффициента a определяет направление открытия параболы: если a положительное, парабола открывается вверх, если отрицательное - вниз.
Значение коэффициента a определяет также степень крутизны параболы: чем больше значение a (по модулю), тем более узкая и крутая парабола, и наоборот.
Таким образом, коэффициент a существенно влияет на характер и форму графика уравнения квадратного трехчлена.
Функции и значения коэффициента a
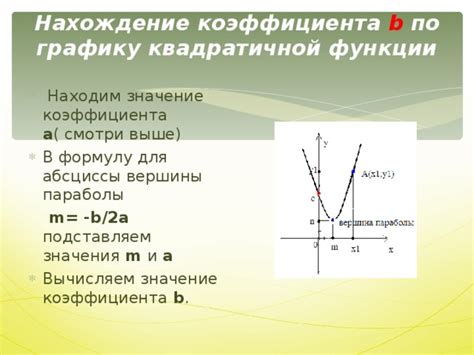
Коэффициент a в уравнении квадратичной функции ax^2 + bx + c определяет, какая часть графика функции располагается над или под осью абсцисс.
Если a > 0, график функции направлен вверх и функция имеет минимум. Если a
Значение коэффициента a также определяет степень открытости параболы: чем больше |a|, тем более узкая парабола.
Влияние коэффициента a на форму графика параболы
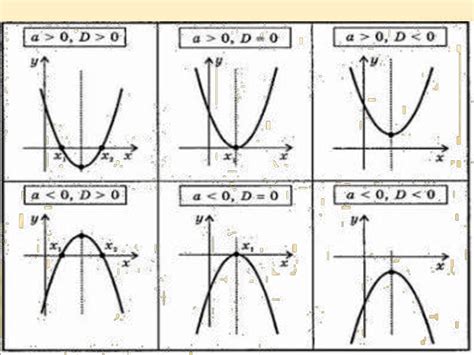
Коэффициент a в уравнении квадратного трёхчлена ax^2 + bx + c определяет, какой будет формы график параболы.
1. Если a > 0, то график параболы будет направлен вверх.
2. Если a
Таким образом, знак коэффициента a определяет ориентацию параболы относительно оси x и влияет на ее выпуклость или вогнутость.
Взаимосвязь между коэффициентами a, b и c в квадратном уравнении

Коэффициент a: определяет, насколько быстро увеличивается или уменьшается парабола, а также направление ее открытия.
Коэффициент b: влияет на положение вершины параболы и направление сдвига по оси x.
Коэффициент c: определяет положение параболы по оси y и ее пересечение с осью ординат.
Из взаимосвязи между этими коэффициентами следует, что изменение любого из них влияет на форму и положение графика квадратного уравнения.
Вопрос-ответ

Что означает коэффициент с в уравнении ax^2 + bx + c?
Коэффициент c в уравнении ax^2 + bx + c представляет собой свободный член или постоянную часть уравнения. Он отвечает за константный член в квадратном уравнении и определяет точку пересечения графика параболы с осью ординат.
Зачем нужен коэффициент c в квадратном уравнении?
Коэффициент c в уравнении ax^2 + bx + c играет важную роль, так как он определяет точку пересечения параболы, заданной уравнением, с осью ординат. Он является свободным членом и указывает на значение функции при x=0.
Какова роль коэффициента c в квадратном уравнении?
Коэффициент c в уравнении ax^2 + bx + c отвечает за свободный член и позволяет определить смещение параболы относительно оси ординат. Значение c указывает на точку, где график параболы пересекает ось y или ось ординат.
Какой смысл имеет коэффициент c в квадратном уравнении?
Коэффициент c в уравнении ax^2 + bx + c является постоянным членом и отражает значение функции при x=0. Он определяет смещение параболы вдоль оси ординат и позволяет вычислить точку пересечения с осью y. Иными словами, он задает базовое значение функции без учета остальных коэффициентов.



