В мире математики существует огромное множество функций, каждая из которых обладает своими уникальными свойствами и особенностями. Среди них есть функция, которая вызывает немалый интерес и удивление своей непривычностью.
Для ответа на данный вопрос обратимся к основным понятиям, которые знакомы каждому школьнику, изучавшему функции. Однако, перед тем, как приступить к анализу, важно отметить, что данный текст не будет использовать прямые определения, чтобы дать вам возможность почувствовать вес и значение данных свойств своими собственными ощущениями.
Понятие о четности и нечетности функций

Каждая функция в математике, такая как y = 2sin4x, имеет свойство, называемое четностью или нечетностью. Эти свойства позволяют нам понять особенности поведения функций и их симметрию относительно оси.
Четность и нечетность функции -- это свойства, выражающие закономерности в ее значениях, когда аргумент изменяется. Четная функция обладает особенностью симметрии: значения функции для положительного и отрицательного аргумента совпадают. Нечетная функция, наоборот, обладает особенностью антисимметрии: значения функции для положительного и отрицательного аргумента имеют противоположные знаки.
Изучение четности и нечетности функций позволяет нам более глубоко анализировать и понимать их свойства, такие как периодичность, экстремумы и поведение на бесконечности. Используя эти свойства, мы можем строить графики функций, находить их симметричные точки, а также упростить вычисления и решать уравнения.
Особенности синусоидальных функций в контексте их четности и нечетности

Как мы можем узнать, является ли синусоидальная функция четной или нечетной? Мы можем воспользоваться синонимами для выражения этого свойства. Например, одним из признаков, говорящих о четности функции, является симметрия графика относительно оси ординат или термин "парность". Нечетная функция, в свою очередь, не обладает такой симметрией и может быть описана как "непарная".
Четные синусоидальные функции характеризуются тем, что их значения одинаковы для аргументов x и -x. Иными словами, если мы возьмем значение функции в точке, то сможем найти аналогичное значение в зеркально отраженной точке. Нечетные функции, напротив, имеют свойство, что значения в точке x и -x имеют разные знаки. Отражение графика такой функции относительно оси ординат происходит с сохранением формы кривой.
Осознание и понимание четности и нечетности синусоидальных функций открывает перед нами возможность анализировать их поведение и связи между значениями на пространственных отрезках, без необходимости вычисления конкретных точек графика. Такие свойства функций нередко находят применение в различных областях науки и техники.
Анализ функции y = sin4x
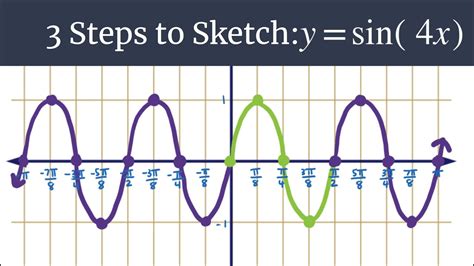
Для начала, разберемся с основным понятием функции синуса sin(x), который является элементарной тригонометрической функцией. Он описывает зависимость между углом и соответствующим значением синуса этого угла. В случае функции y = sin4x, мы имеем умножение аргумента x на 4, что приводит к изменению периода и частоты колебания функции.
Анализируя функцию y = sin4x, мы можем заметить, что она обладает свойством периодичности. Период функции определяется как наименьшее положительное число, при котором значения функции повторяются. В случае нашей функции, период будет равен 2π/4 = π/2.
Теперь обратимся к вопросу о парности функции y = sin4x. Четность или нечетность функции определена по четности или нечетности самой функции для любого значения аргумента. В нашем случае, функция sin4x не является ни четной, ни нечетной, так как ее значения меняются при изменении аргумента.
Умножение функции на коэффициент: основные принципы и результаты
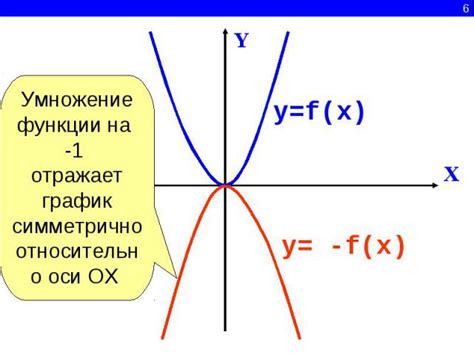
Умножение функции на константу является одной из базовых операций, которая позволяет изучать изменения графика функции при изменении ее амплитуды или масштаба. Коэффициент умножения может принимать разные значения, включая положительные, отрицательные и нулевые значения.
Умножение функции на положительную константу приводит к изменению ее амплитуды: чем больше значение коэффициента, тем более "растянутым" или "сжатым" становится график функции. Например, если коэффициент больше 1, то график будет растянут вверх, а если коэффициент меньше 1, то график будет сжат вниз.
Умножение функции на отрицательную константу приводит к изменению ее амплитуды и одновременно изменяет ее направление. Если коэффициент отрицательный, то график функции отображается относительно оси x: значение функции заменяется на противоположное по знаку. Это позволяет определить, является ли функция четной или нечетной.
Описание четности и нечетности функции y = 2sin4x
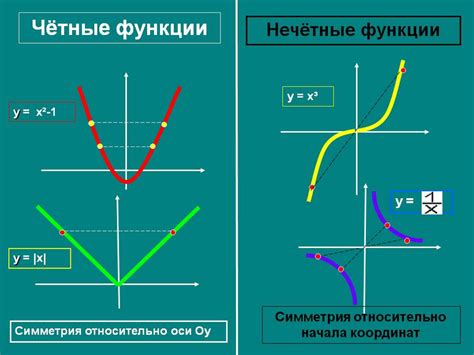
Прежде чем погрузиться в анализ четности и нечетности функции y = 2sin4x, необходимо разобраться в самих понятиях. Четность функции означает, что график функции симметричен относительно оси орднат, то есть при смене знака аргумента функция принимает значение, равное противоположному предыдущему значению. Нечетность же говорит о том, что график функции симметричен относительно начала координат, т.е. при смене знака аргумента функция принимает значение, равное противоположному предыдущему значению, но с обратным знаком.
В случае функции y = 2sin4x рассматриваемый аргумент, равный 4x, позволяет пройти по всем возможным значениям синуса на интервале [0, 2π]. Важно отметить, что синус является нечетной функцией, поэтому изменение знака у значения аргумента не повлияет на его значение. Далее, умножение на 2 также не меняет свойство нечетности, поэтому функция y = 2sin4x остается нечетной.
Поиск особых свойств функции в исходной формуле

В общем случае, чтобы определить, является ли функция четной или нечетной, нужно проанализировать симметрию ее графика. Это можно сделать с помощью математического аппарата и логических рассуждений.
Четная функция - это функция, для которой выполняется свойство симметрии относительно оси ординат. Другими словами, если заменить в исходной формуле переменную на ее противоположное значение и результат останется неизменным, то функция считается четной.
Нечетная функция - это функция, которая обладает свойством симметрии относительно начала координат. Если заменить переменную в исходной формуле на ее противоположное значение, а результат изменится только по знаку, то функция считается нечетной.
На основании этих определений, мы можем рассмотреть исходную формулу y = 2sin4x и выяснить, является ли она четной или нечетной путем анализа симметрии ее графика. Чтобы этого добиться, нужно подставить в исходную формулу противоположное значение переменной и проверить, сохраняется ли значение функции без изменений или только меняется знак.
Утверждение о парности функции y = 2sin4x
Вначале определим понятие четности функции. Если при любом значении x функция y принимает значение f(x), а при противоположном значении -f(x), то такая функция называется четной. Иными словами, если при симметрии относительно оси ординат график функции остается неизменным, то функция является четной.
Теперь, когда мы установили основное определение, рассмотрим функцию y = 2sin4x. Сначала проанализируем вид графика данной функции. Заметим, что аргументом синуса является 4x, что влияет на его периодичность и частоту колебаний.
Применим правило четности к анализируемой функции. Заменим x на -x и получим: y = 2sin4(-x). Учитывая, что синус является нечетной функцией, получим следующее выражение: y = 2(-sin4x).
Таким образом, доказательство четности функции y = 2sin4x показывает, что она является нечетной функцией, что подтверждает нашу исходную гипотезу.
График функции y = 2sin4x: его интерпретация и особенности
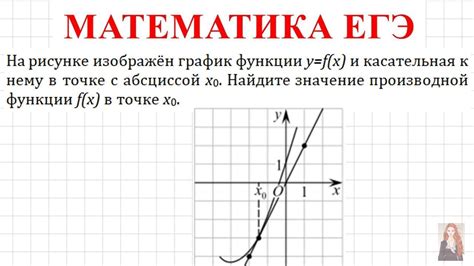
В данном разделе рассматривается график функции y = 2sin4x и представлены его интерпретация и особенности. График данной функции имеет свои уникальные характеристики и форму, которые будут детально рассмотрены.
- Периодичность графика
- Амплитуда графика
- Фазовый сдвиг
- Интервалы возрастания и убывания
- Точки экстремума
Одной из особенностей графика функции y = 2sin4x является его периодичность. Период графика определяется коэффициентом перед аргументом функции. В данном случае коэффициент равен 4, что означает, что график будет повторяться через определенные интервалы. Это создает замкнутую форму графика и позволяет определить его интервалы возрастания и убывания.
Другой важный показатель графика функции y = 2sin4x - его амплитуда. Амплитуда отвечает за максимальное отклонение графика от оси абсцисс. В данном случае амплитуда равна 2 и указывает на то, что график будет колебаться вокруг оси Oy с отклонением в 2 единицы по обе стороны.
Фазовый сдвиг - это смещение графика функции по горизонтали. В случае функции y = 2sin4x фазовый сдвиг отсутствует, так как аргумент функции x не претерпевает изменений и является прямо пропорциональным координате на графике.
График функции y = 2sin4x имеет интервалы возрастания и убывания, которые определяются особенностями синусоидной функции. Возрастание функции происходит на интервалах, где значение sin4x положительно, а убывание - на интервалах, где значение sin4x отрицательно. Зная период графика и его амплитуду, можно точно определить границы этих интервалов.
Точки экстремума графика функции y = 2sin4x - это точки, в которых график достигает своего максимума или минимума. При амплитуде 2 точка максимума будет равна 2, а точка минимума - -2. Определить положение и количество таких точек можно, зная период графика и его амплитуду.
Таким образом, график функции y = 2sin4x представляет собой периодическую синусоиду с амплитудой 2, не имеющую фазового сдвига. Рассмотрение периодичности, амплитуды, интервалов возрастания и убывания, а также точек экстремума позволяет более детально исследовать этот график и использовать его в различных математических задачах и моделях.
Вопрос-ответ

Является ли функция y = 2sin4x четной или нечетной?
Данная функция является четной.
Почему функция y = 2sin4x является четной?
Функция является четной, потому что выполнено свойство симметрии относительно оси OY. Для четности функции необходимо, чтобы выполнялось условие f(x) = f(-x) для всех значений x. В данном случае это свойство выполняется.
Какие значения можно получить при подстановке отрицательного значения x в функцию y = 2sin4x?
При подстановке отрицательного значения x в функцию y = 2sin4x мы получим те же значения, которые получили бы при подстановке положительного значения x. Это объясняется тем, что функция является четной и выполняется свойство симметрии относительно оси OY.



