arccos (также известный как обратный косинус) является одной из тригонометрических функций, обратной косинусу. Изучение этой функции позволяет нам понять, как она работает и какие значения принимает. В данном случае проанализируем выражение arccos 1/2 и постараемся разобраться, почему стоит обратить на него внимание.
Значение arccos 1/2 имеет особое значение в математике и при решении различных задач. Это выражение отражает угол, косинус которого равен 1/2. Изучение этого значения позволяет нам лучше понять, как работает тригонометрия и какие связи существуют между различными функциями.
Итак, анализ arccos 1/2 даст нам возможность глубже вникнуть в мир тригонометрии и расширить наши знания в этой области математики. Рассмотрим подробнее это выражение и его значение, чтобы лучше понять его применение и важность в наших расчетах и исследованиях.
Анализ выражения arccos 1/2

Таким образом, arccos 1/2 равен углу α, такому что cos(α) = 1/2. В случае тригонометрических функций углы измеряются в радианах.
Для нахождения конкретного значения α можно использовать таблицы тригонометрических функций или калькулятор с функцией arccos. В случае arccos 1/2, мы получаем α ≈ π/3 (60 градусов) или α ≈ 5π/3 (300 градусов).
Понятие арккосинуса
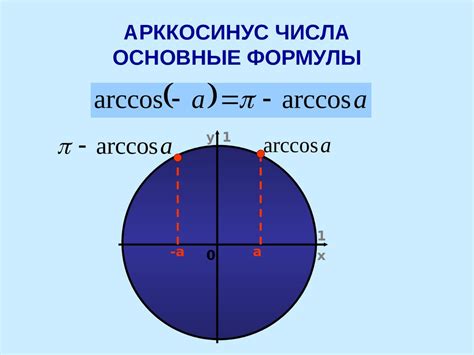
Значение arccos зависит от диапазона значений, обычно в интервале от 0 до π. Важно помнить, что arccos имеет ограничения на вводимые значения: оно может принимать только значения от -1 до 1. Поэтому для ввода числа вне этого диапазона необходимо использовать расширенную математическую астрономию или комплексные числа.
Понимание арккосинуса важно при решении задач по тригонометрии и геометрии, а также в математическом анализе и физике. Знание свойств и особенностей arccos позволяет более глубоко понять функции и их взаимосвязи.
Основное значение угла

Расчет арккосинуса
Так как косинус угла равен отношению прилежащего к гипотенузе в прямоугольном треугольнике, то для arccos 1/2 можем использовать прямоугольный треугольник с катетом равным 1 и гипотенузой равной 2.
Из этого следует, что косинус угла, равного arccos 1/2, равен 1/2. Таким образом, угол arccos 1/2 равен 60 градусам или π/3 радианам.
Свойства выражения

Рассмотрим выражение arccos 1/2. Значение этого выражения равно углу в радианах, косинус которого равен 1/2. Таким образом, arccos 1/2 равно pi/3 (или 60 градусов).
| arccos(1/2) | = | pi/3 | (60 градусов) |
Практическое применение

Также значение arccos(1/2) может применяться в телекоммуникациях для расчета фазовых сдвигов между сигналами, в физике для определения углов отражения или преломления света, а также в других областях науки и техники.
Геометрическая интерпретация
Для понимания геометрической интерпретации выражения arccos 1/2 достаточно взглянуть на график функции обратного косинуса в диапазоне значений от 0 до π. Так как arccos представляет обратную функцию к косинусу, мы ищем угол, косинус которого равен 1/2.
Угол, удовлетворяющий уравнению cos(x) = 1/2, это угол π/3 (60 градусов). Поэтому arccos(1/2) равен π/3 или 60 градусов. Геометрически это означает, что косинус угла π/3 равен 1/2.
Поиск альтернативных выражений

Арккосинус и другие тригонометрические функции
Формула arccos(x) = y означает, что arccosинус x равен y, где x – значение косинуса, а y – угол в радианах от 0 до π. Например, arccos(1/2) = π/3, так как косинус угла π/3 равен 1/2.
Тригонометрические функции широко применяются в науке, технике, физике, анализе данных и других областях. Понимание их свойств позволяет решать разнообразные задачи и проводить качественные исследования.
Вопрос-ответ

Что такое arccos 1/2 и как его можно интерпретировать?
Выражение arccos 1/2 означает обратный косинус угла, значение косинуса которого равно 1/2. Это эквивалентно нахождению угла, косинус которого равен 1/2. Такой угол составляет π/3 радиан или 60 градусов. Поэтому arccos 1/2 равен π/3 или 60°.
Зачем нужно анализировать значение arccos 1/2 и в каких случаях это может оказаться полезным?
Анализ выражения arccos 1/2 полезен для понимания тригонометрических функций и соответствующих углов. Это может пригодиться при решении задач математического моделирования, в геометрии, физике или инженерных расчетах, где требуется точное определение углов. Знание значения arccos 1/2 поможет правильно интерпретировать результаты решения задач.
Может ли значение arccos 1/2 быть применено на практике и как это может отразиться на повседневной жизни?
Знание значения arccos 1/2 может быть полезным, например, при вычислении углов для построения объектов, в навигации и картографии, в компьютерной графике, при разработке игр или анимации. Таким образом, умение анализировать и применять arccos 1/2 может найти применение в различных сферах деятельности, где требуется работа с углами и тригонометрическими функциями.



