Осевая симметрия – одно из важных понятий геометрии, которое позволяет нам понять, как объекты отражаются относительно определенной оси. В данной статье мы рассмотрим случай осевой симметрии, когда объекты симметричны относительно двух пересекающихся прямых.
Пересекающиеся прямые – это две прямые, которые имеют общую точку пересечения. Если объекты симметричны относительно таких прямых, то каждая точка объекта будет равноудалена от обеих прямых. Такое свойство позволяет нам определить отражение объекта относительно пересекающихся прямых.
Изучение осевой симметрии важно не только для понимания геометрических принципов, но и для решения задач в различных областях науки и техники. Понимание осевой симметрии пересекающихся прямых поможет значительно упростить решение проблем, связанных с отражением объектов и построением симметричных фигур.
Осевая симметрия: принцип действия
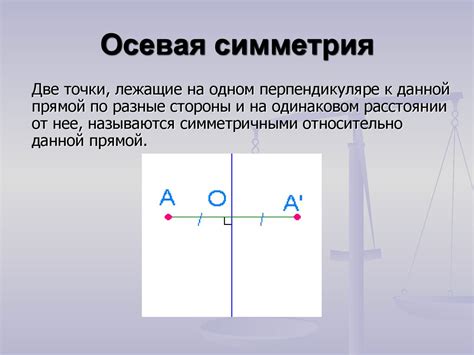
Пересекающиеся прямые и их роль
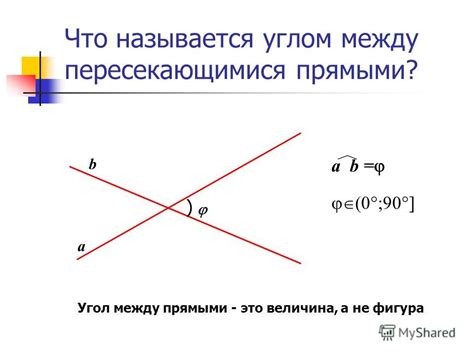
- Пересекающиеся прямые могут определять углы между собой, что позволяет решать задачи на нахождение угловых мер или на построение треугольников с заданными свойствами.
- Они также используются для описания расположения различных объектов на плоскости, например, расстояние между двумя прямыми или их взаимное расположение.
- При изучении пересекающихся прямых важно учитывать их свойства, например, связь между углами, образованными пересекающими прямыми, или использование пересекающихся прямых для построения прямоугольников и других фигур.
Вопрос-ответ

Что такое осевая симметрия и как она связана с пересекающимися прямыми?
Осевая симметрия - это тип симметрии, при котором объект или фигура располагается относительно осевой линии, так что любая точка на одной стороне отражается симметрично относительно этой оси на другую сторону. В случае пересекающихся прямых, осевая симметрия может проходить через точку и перпендикулярна плоскости, образованной этими прямыми.
Как определить, что две пересекающиеся прямые обладают осевой симметрией?
Для того чтобы две прямые обладали осевой симметрией, существует несколько способов. Один из них - найти осевую линию, которая перпендикулярна к плоскости, образованной прямыми, и проходит через точку их пересечения. Если каждая точка на одной прямой имеет симметричную точку на другой прямой относительно этой линии, то прямые обладают осевой симметрией.
Какие свойства обладают фигуры, симметричные относительно точки пересечения двух пересекающихся прямых?
Фигуры, симметричные относительно точки пересечения двух пересекающихся прямых, обладают такими свойствами: они равновелики и равноотстоят от осей симметрии, а также могут быть отражены относительно этих осей без искажения изначальной фигуры.



