Уравнение вида х^2 - 16x + 26 является квадратным уравнением, которое может иметь один, два или ни одного корня в зависимости от дискриминанта.
Дискриминант квадратного уравнения определяется по формуле D = b^2 - 4ac, где a, b и c - коэффициенты уравнения. Если дискриминант больше нуля, то у уравнения два действительных корня. Если дискриминант равен нулю, то у уравнения один действительный корень. Если дискриминант меньше нуля, то у уравнения нет действительных корней, но есть комплексные корни.
Для уравнения х^2 - 16x + 26 коэффициенты a = 1, b = -16 и c = 26. Найдем дискриминант: D = (-16)^2 - 4*1*26. После расчетов получим D = 256 - 104 = 152. Таким образом, дискриминант равен 152, что больше нуля. Значит, уравнение имеет два действительных корня.
Решение квадратного уравнения

Если D > 0, то уравнение имеет два различных корня. Если D = 0, то уравнение имеет один корень. Если D
В случае уравнения x^2 - 16x + 26, коэффициенты a = 1, b = -16, c = 26.
Вычисляем дискриминант: D = (-16)^2 - 4*1*26 = 256 - 104 = 152.
Поскольку D > 0, уравнение имеет два различных действительных корня.
Нахождение дискриминанта
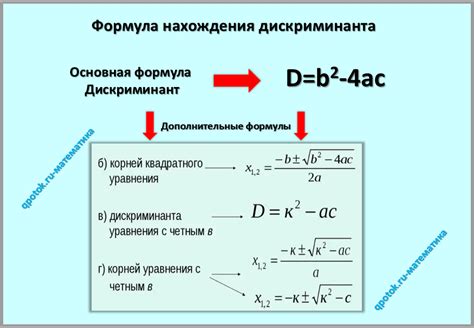
Для того чтобы определить имеет ли уравнение корни, необходимо вычислить дискриминант по формуле:
Дискриминант (D) = b^2 - 4ac
Где a, b, c - коэффициенты уравнения вида ax^2 + bx + c = 0.
Для уравнения x^2 - 16x + 26:
а = 1, b = -16, c = 26.
Подставляем значения в формулу дискриминанта:
D = (-16)^2 - 4*1*26
D = 256 - 104
D = 152
После вычисления дискриминанта нужно проанализировать его значение:
1. Если D > 0, то уравнение имеет два различных корня.
2. Если D = 0, то уравнение имеет один корень (корень кратности два).
3. Если D
В данном случае, так как D = 152 (D > 0), уравнение x^2 - 16x + 26 имеет два различных вещественных корня.
Определение количества корней
Если D > 0, то у уравнения два различных корня.
Если D = 0, то у уравнения один корень (уравнение имеет кратный корень).
Если D
Таким образом, для уравнения х^2 - 16x + 26 дискриминант равен 16^2 - 4*1*26 = 16, что больше нуля. Следовательно, у уравнения два различных корня.
Проверка утверждения

Чтобы определить, имеет ли уравнение корни, нужно решить его по формуле:
Дискриминант D = b^2 - 4ac
Если D>0, то у уравнения есть два различных корня.
Если D=0, то у уравнения есть один корень (корни совпадают).
Если D
Для уравнения х^2 - 16x + 26:
a = 1, b = -16, c = 26
Вычислим дискриминант: D = (-16)^2 - 4*1*26 = 256 - 104 = 152
Так как D>0, то у уравнения есть два различных корня.
Примеры решения
2. Так как D > 0, то уравнение имеет два действительных корня.
3. Найдем корни уравнения, используя формулу корней квадратного уравнения: x = (-(-16) ± √152) / 2*1.
4. Получаем два корня: x1 = (16 + √152) / 2 ≈ 14.29, x2 = (16 - √152) / 2 ≈ 1.71.
Таким образом, уравнение x^2 - 16x + 26 имеет два действительных корня: x1 ≈ 14.29 и x2 ≈ 1.71.
Вопрос-ответ

Как определить, имеет ли уравнение х^2 - 16x + 26 корни?
Чтобы определить, имеет ли уравнение х^2 - 16x + 26 корни, нужно рассмотреть дискриминант этого уравнения. Дискриминант вычисляется по формуле D = b^2 - 4ac, где a, b, c - коэффициенты уравнения. В данном случае, у нас a = 1, b = -16, c = 26. Подставляем значения и вычисляем: D = (-16)^2 - 4*1*26 = 256 - 104 = 152. Так как дискриминант положителен (D > 0), уравнение имеет два различных вещественных корня.
Какие шаги нужно предпринять, чтобы найти корни уравнения х^2 - 16x + 26?
Для нахождения корней уравнения х^2 - 16x + 26 необходимо применить формулу корней квадратного уравнения: x = (-b ± √D) / (2a), где D - дискриминант, а, b, c - коэффициенты уравнения. В данном случае, D = 152 (см. предыдущий ответ). Подставляем значения коэффициентов a = 1, b = -16, c = 26 и находим корни уравнения.
Какой метод можно применить, чтобы определить, имеет ли уравнение х^2 - 16x + 26 вещественные корни?
Для определения вещественных корней уравнения х^2 - 16x + 26 следует посчитать дискриминант. Если дискриминант больше нуля, то у уравнения есть два вещественных корня. В нашем случае дискриминант равен 152, что говорит о существовании двух вещественных корней у данного уравнения.
Какие выводы можно сделать относительно корней уравнения х^2 - 16x + 26, основываясь на его дискриминанте?
Исходя из значения дискриминанта (152), можно утверждать, что уравнение х^2 - 16x + 26 имеет два вещественных корня. Это означает, что график уравнения пересекает ось Х дважды и уравнение имеет два различных решения. Дискриминант позволяет нам понять, сколько корней имеет уравнение и их тип (вещественные или комплексные).



