Треугольник - одна из основных фигур в геометрии, и его высоты играют важную роль в решении различных задач.
Многие студенты задаются вопросом о том, где располагаются высоты треугольника относительно самой фигуры. Однако, есть ли утверждение, что высоты всегда лежат внутри треугольника?
Давайте разберемся в этом важном геометрическом вопросе, который поможет расширить наши знания о треугольниках и их свойствах.
Высоты треугольника
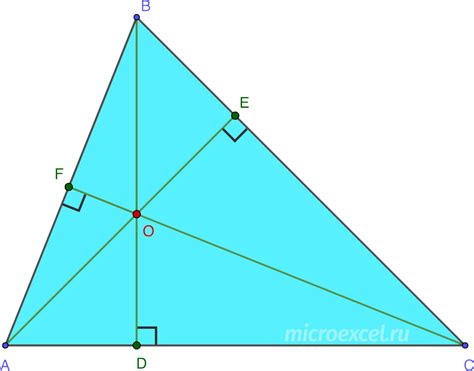
Высоты треугольника могут лежать как внутри треугольника, так и за его пределами, в зависимости от вида треугольника.
В равностороннем треугольнике все высоты пересекаются в одной точке, которая одновременно является центром вписанной окружности.
В любом треугольнике точка пересечения высот называется ортоцентром.
Понятие высот треугольника

Геометрическое изучение треугольника
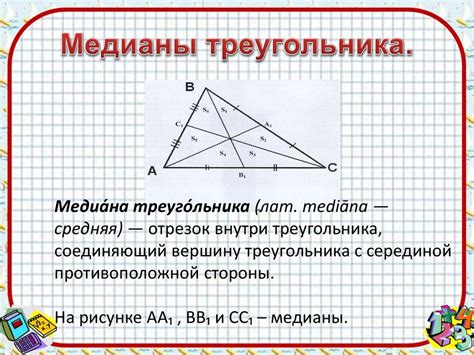
Важно помнить, что высоты треугольника всегда лежат в его внутренней области. Это следует из свойства треугольника, что высота, проведенная из вершины, перпендикулярна к основанию и лежит внутри фигуры. Знание этого свойства позволяет более глубоко изучать геометрию треугольников и строить различные геометрические рассуждения и доказательства.
Геометрия треугольника играет важную роль в математике и на практике, позволяя решать задачи как в чистой математике, так и в различных её приложениях.
Математические свойства треугольника

1. Сумма углов в треугольнике всегда равна 180 градусов. Это называется теоремой о сумме углов в треугольнике.
2. Высоты треугольника пересекаются в одной точке – ортоцентре.
3. Биссектрисы углов треугольника также пересекаются в одной точке, называемой центром вписанной окружности.
4. Высота, опущенная из вершины на основание, делит треугольник на два подобных треугольника в отношении, равном отношению сторон треугольника.
Эти и другие свойства треугольника помогают понять его структуру и использовать их для решения задач по геометрии.
Теорема о лежащих высотах
Одна из важных теорем, связанных с высотами треугольника, утверждает, что все высоты треугольника пересекаются в одной точке, называемой ортоцентром. Эта точка лежит внутри треугольника, если треугольник остроугольный, на его сторонах, расстояния от вершин до ортоцентра оба разделены пополам высотами, а также сумма квадратов отрезков от вершин до ортоцентра равна сумме квадратов сторон треугольника.
Геометрическое доказательство теоремы
Для доказательства того, что высоты треугольника всегда лежат в его внутренней области, рассмотрим произвольный треугольник ABC. Проведем высоты AD, BE и CF, которые пересекаются в точке H (точке пересечения высот называется ортоцентр).
Пусть точка H лежит внутри треугольника ABC. Тогда обратимся к треугольникам AHD и AHB. Так как AH и AD являются высотами этих треугольников, то по критерию перпендикулярности высот получаем, что угол HAD = угол HAB = 90 градусов. То есть точки D и B в данном случае лежат на сторонах AC и BC треугольника ABC.
Повторяя такие рассуждения для оставшихся сторон треугольника, получаем, что все высоты треугольника ABC пересекаются внутри его области, что и требовалось доказать.
Следствия из теоремы о высотах

| 1. | Высоты треугольника всегда пересекаются в одной точке, называемой ортоцентром. |
| 2. | Ортоцентр может лежать как внутри треугольника, так и вне его, в зависимости от вида треугольника. |
| 3. | Точка пересечения высот треугольника делит каждую из высот в определенном отношении, называемом правилом Шевы. |
Примеры применения теоремы в решении задач
Рассмотрим задачу: дан треугольник ABC. Докажем, что высоты этого треугольника пересекаются в одной точке (ортоцентре). Используем теорему о пересечении высот треугольника.
1. Пусть H - ортоцентр треугольника ABC, h1, h2, h3 - высоты, опущенные на стороны треугольника из вершин A, B, C соответственно.
2. Тогда по теореме о пересечении высот треугольника H лежит на высоте h1, проведенной из вершины A, на высоте h2 из вершины B и на высоте h3 из вершины C.
3. Следовательно, все три высоты треугольника ABC пересекаются в одной точке - ортоцентре H.
Таким образом, теорема о пересечении высот треугольника позволяет решать задачи связанные с ортоцентром треугольника и его высотами.
1. Высоты треугольника всегда лежат в его внутренней области.
2. Высоты перпендикулярны соответствующим сторонам треугольника.
3. Пересечение высот в одной точке называется ортоцентром.
4. Ортоцентр может лежать как внутри треугольника, так и за его пределами в зависимости от взаимного расположения вершин.
Вопрос-ответ

Правда ли, что высоты треугольника всегда лежат внутри треугольника?
Да, это верно. Вершина высоты треугольника соединяется с противоположным углом, а высота перпендикулярна соответствующей стороне. Таким образом, высоты всегда пересекаются внутри треугольника, а не за его пределами.
Как можно доказать, что высоты треугольника лежат внутренней области?
Для доказательства этого факта можно воспользоваться геометрическими свойствами высот треугольника. К примеру, можно использовать свойство прямых углов: каждая высота образует прямой угол с соответствующей стороной треугольника. Также можно провести доказательство с помощью свойства перпендикулярных прямых и свойств треугольников. В итоге, высоты треугольника всегда должны лежать в его внутренней области.



