Взаимное расположение точек на прямой является одной из базовых концепций в математике, которая позволяет определить взаимное положение точек на прямой относительно друг друга. Эта концепция является основой для понимания понятий направления и расстояния на прямой, что находит широкое применение в различных областях математики и ее приложениях.
Взаимное расположение точек может быть определено по разным критериям, таким как их порядковый номер на прямой, расстояние между ними или их направление относительно друг друга. Рассмотрение этого вопроса поможет развить интуитивное понимание пространственных отношений и способствует решению задач как в школьной математике, так и в более сложных математических моделях.
Изучение взаимного расположения точек на прямой
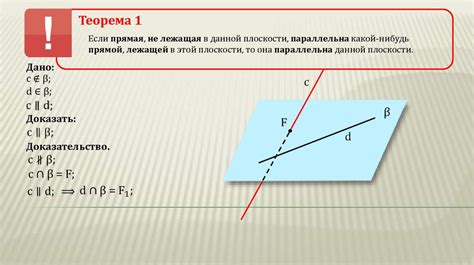
| Положение точек | Описание |
|---|---|
| Точка А слева от точки В | Если А меньше B, то А находится левее от B на прямой |
| Точка А справа от точки В | Если А больше B, то А находится правее от B на прямой |
| Точки А и В совпадают | Когда А равно B, то они находятся на одной и той же точке на прямой |
Суть задачи в математике

Различные случаи взаимного расположения

Взаимное расположение точек на прямой может быть различным в зависимости от их координат. Вот некоторые распространенные случаи:
- Точки находятся в порядке возрастания: если координаты точек упорядочены по возрастанию (точка A левее точки B), то точка A расположена левее точки B на числовой прямой.
- Точки находятся в порядке убывания: если координаты точек упорядочены по убыванию (точка A правее точки B), то точка A расположена правее точки B на числовой прямой.
- Точки совпадают: если координаты точек равны (A = B), то точки совпадают и находятся в одной точке на числовой прямой.
Примеры решения задачи
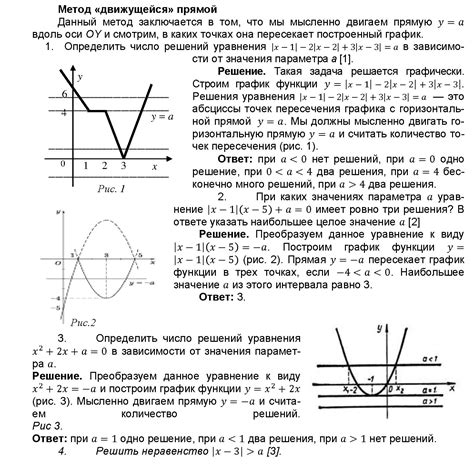
Пример 1: Пусть на числовой прямой даны точки А, В и С, причем А находится левее В, В находится левее С. Тогда расположение точек на прямой будет следующим: A --- B --- C.
Пример 2: Даны точки М, Н и О на числовой прямой, причем М левее Н, Н левее О. Тогда порядок расположения точек будет таков: М --- Н --- О.
Значение в практической геометрии

Знание взаимного расположения точек на прямой играет важную роль в решении различных задач практической геометрии. Например, при построении отрезков, отсчёте расстояний, определении направлений или углового положения объектов.
Понимание того, как точки расположены на прямой, помогает в работе с отрезками, положением прямых и плоскостей, построении графиков и моделировании трехмерных объектов. Знание базовых принципов взаимного расположения точек позволяет более эффективно решать задачи, связанные с геометрией.
Резюме: важность понимания сущности

Понимание сути взаимного расположения точек на прямой поможет вам стать более уверенным в решении математических задач и применении математических методов в повседневной жизни.
Вопрос-ответ

Что такое взаимное расположение точек на прямой?
Взаимное расположение точек на прямой определяет, как точки расположены относительно друг друга на одной прямой. Точки могут быть соседними, лежать на одной прямой, быть разделенными другими точками и т.д.
Какие основные типы взаимного расположения точек на прямой существуют?
Основные типы взаимного расположения точек на прямой - соседние точки, коллинеарные точки (лежащие на одной прямой), точки разделенные другими точками, точки между другими точками и прочие комбинации взаимного расположения.
Как определить, что две точки лежат на одной прямой?
Для того чтобы определить, что две точки лежат на одной прямой, необходимо проверить условие коллинеарности. Для этого можно использовать теорему о трех точках: если три точки лежат на одной прямой, то любые две из них также будут лежать на этой прямой.
Можете привести примеры взаимного расположения точек на прямой?
Конечно! Примеры взаимного расположения точек на прямой могут быть разнообразными: две точки, несоседние и не коллинеарные; три точки, лежащие на одной прямой; точки, разделенные другой точкой и так далее. Все эти примеры являются важными для понимания пространственных отношений между точками.



