Есть одно математическое выражение, которое нашло широкое применение в науке и жизни, став центральной составляющей многих графиков и моделей. Это формула, описывающая квадратичную функцию и ее свойства. Она позволяет нам анализировать и предсказывать поведение различных систем и процессов. Рассмотрим основные черты этой формулы и попробуем постичь ее суть, не используя ее устоявшихся терминов и определений.
Когда мы вспоминаем наши школьные занятия по математике, то, скорее всего, всплывает в голове памятная картина: график функции, заданной формулой y = x^2. Эта картина привлекала наше внимание своей округлостью и симметрией. Но что на самом деле заключено в этой формуле? Зачем она нужна и как она работает? Попытаемся разобраться в этом.
Квадратичная функция - это математическое выражение, которое связывает между собой две переменные: независимую переменную x и зависимую переменную y. По формуле y = x^2 мы можем вычислить значение y, зная значение x. Но самое интересное в этой формуле - то, как y зависит от x. Она позволяет нам построить график, где ось x отображает значения x, а ось y - значения y. И вот здесь начинается интересное исследование.
Определение и основные характеристики функции у = х в квадрате
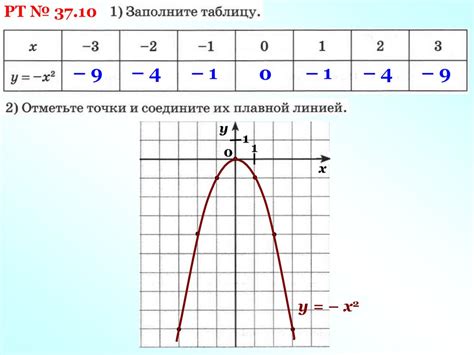
Когда мы говорим о функции у = х в квадрате, мы относимся к классу математических функций, где значение у зависит от значения х, возведенного в квадрат. Такая функция применяется во многих областях науки и инженерии, а также имеет особый статус в математике.
Важной характеристикой функции у = х в квадрате является то, что она представляет собой график параболы. Парабола имеет ось симметрии, которая проходит через ее вершину и нули функции находятся на равных расстояниях от вершины. Коэффициент при х в квадрате определяет, насколько "широкой" или "узкой" будет парабола.
Ветви параболы могут открываться вверх или вниз, в зависимости от знака коэффициента при х в квадрате. Если коэффициент положительный, парабола будет направлена вверх, а если отрицательный - вниз. Вершина параболы является крайней точкой графика и представляет собой точку минимума или максимума, в зависимости от направления параболы.
Кроме того, функция у = х в квадрате обладает равенством симметрии. Это означает, что график функции симметричен относительно оси ординат, т.е. если мы знаем значение функции для положительного значения х, мы автоматически знаем значение функции для отрицательного значения х.
- Функция у = х в квадрате представляет собой график параболы
- Основные характеристики функции - вершина, ось симметрии и нули
- Знак коэффициента при х в квадрате определяет направление параболы
- Функция обладает равенством симметрии относительно оси ординат
Как устроена функция с квадратным законом
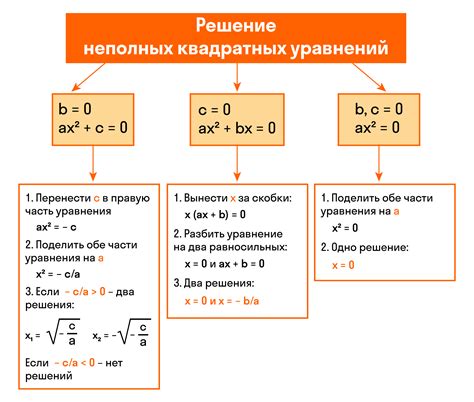
В данном разделе мы рассмотрим принцип работы функции, которая описывается квадратной зависимостью по переменной. Эта функция имеет свои особенности и используется во множестве прикладных областей.
Принцип работы
Основная идея принципа работы данной функции заключается в возведении значения переменной во вторую степень. Таким образом, при изменении значения переменной, значение функции будет изменяться нелинейно, а именно квадратично. Это означает, что при увеличении значения переменной, функция будет расти быстрее, а при уменьшении - убывать.
Особенности
Одной из особенностей данной функции является наличие вершины, которая определяет экстремум функции. Если значение переменной, то значение функции будет минимальным. Если значение переменной, то значение функции будет максимальным. Также, функция с квадратным законом может иметь один или два корня, что влияет на форму графика функции.
Интересно отметить, что данная функция находит широкое применение в математике, физике, экономике и других науках. Она позволяет моделировать и описывать ряд явлений и процессов, а также решать различные практические задачи.
Таким образом, принцип работы функции с квадратным законом позволяет учесть нелинейность зависимости между переменными и найти решения для различных задач. Изучение данной функции является важным шагом в понимании основ математики и ее приложений.
Графическое представление функции y = x^2 на плоскости
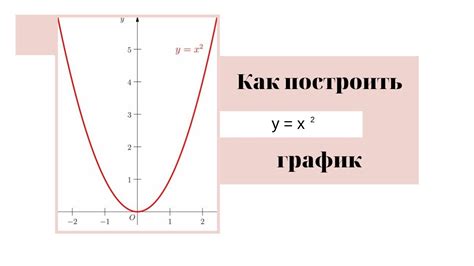
В данном разделе мы рассмотрим визуальное изображение функции y = x^2 на плоскости. Это представление позволяет наглядно увидеть и понять основные особенности и свойства этой функции.
Графическое представление - это способ визуального изображения математических объектов, в данном случае функции y = x^2. При построении графика функции мы отображаем значения аргументов x и соответствующие значения функции y на плоскости. Таким образом, можно наблюдать зависимость между значениями x и соответствующими значениями функции y.
Главная особенность графика функции y = x^2 заключается в том, что он представляет собой параболу. Парабола - это геометрическая фигура в форме дуги, которая имеет ось симметрии и вершину. В случае функции y = x^2 вершина параболы находится в начале координат (0,0) и ось симметрии проходит через эту вершину.
График функции y = x^2 также обладает следующими свойствами:
- Функция является параболой с ветвями, направленными вверх. Изображение графика на плоскости будет расположено только выше оси x.
- Значения функции y неограничены сверху и увеличиваются с ростом значения аргумента x. При x, стремящемся к бесконечности, y также стремится к бесконечности.
- График функции симметричен относительно оси y. То есть, если у нас есть точка (x, y) на графике, то также будет существовать точка (-x, y).
Графическое представление функции y = x^2 помогает визуализировать её особенности и установить взаимосвязи между значениями аргумента x и соответствующими значениями функции y.
Особенности функции y = x^2 в рамках действительных чисел

Функция y = x^2 представляет собой параболу, которая открывается вверх и имеет вершину в точке с координатами (0, 0). Она является симметричной относительно оси ординат и имеет положительные значения на всей числовой прямой.
Одним из важных свойств функции y = x^2 является ее возрастание на всем множестве действительных чисел. Это означает, что с увеличением значения x функция y также увеличивается. Следовательно, для положительных значений x функция y = x^2 будет положительной, а для отрицательных значений x – отрицательной.
Другим важным свойством функции y = x^2 является ее выпуклость вверх. Это означает, что парабола не имеет точек перегиба и кривизна параболы увеличивается при приближении к вершине параболы. Благодаря этому свойству, функция y = x^2 находит применение в оптимизационных задачах, в теории вероятности, а также в физических и экономических моделях.
Таким образом, функция y = x^2 обладает множеством интересных свойств, которые делают ее полезной и востребованной в различных областях. Изучение и анализ данной функции позволяет понять ее особенности и применить ее в практических задачах, что делает ее важной частью математического аппарата.
| Особенности функции y = x^2: |
|---|
| Открывается вверх |
| Симметричность относительно оси ординат |
| Возрастание на всем множестве действительных чисел |
| Выпуклость вверх |
Интерпретация функции y = x^2 в геометрии и физике
В данном разделе мы рассмотрим интересную и многогранную интерпретацию функции y = x^2 в геометрии и физике. Открыв для себя новые грани математических концепций, мы погрузимся в увлекательный мир, где кривая графика функции y = x^2 может иметь различные значения, отражая геометрические формы и законы физики.
1. Геометрия: параболические формы
В геометрии парабола – это плоская кривая, образующаяся при пересечении плоскости с одним неподвижным точечным объектом (фокусом) и всеми точками данной плоскости, равноудаленными от фокуса и прямой, называемой директрисой. Функция y = x^2 именно такую кривую и представляет. Она описывает параболическую форму, которая может быть применена в геометрии для построения различных объектов, таких как мосты, антенны, цветочные вазы и многое другое.
2. Физика: движение и силы
В физике функция y = x^2 находит применение в описании различных явлений, связанных с движением и силами. Мы можем использовать эту функцию для моделирования параболической траектории движения объектов под действием гравитации или других сил. Кривая, описываемая этой функцией, помогает нам понять, как объекты движутся и как законы физики влияют на их траекторию.
Заключение
Интерпретация функции y = x^2 в геометрии и физике демонстрирует ее роль и важность в различных областях науки и практического применения. Параболические формы в геометрии и параболическая траектория движения в физике открывают новые возможности изучения и понимания окружающего мира. Благодаря этим интересным аспектам, мы можем расширить свои знания и взгляды на математику, геометрию и физику.
Применение функции y = x^2 в математических моделях
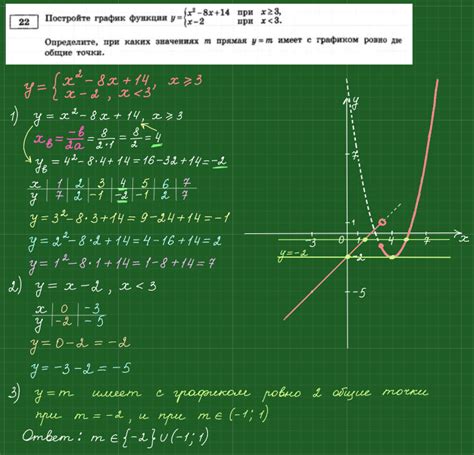
Использование функции y = x^2 в математических моделях:
Математическая функция y = x^2 представляет собой квадратичную функцию, которая находит множество значений y в зависимости от переменной x, возведенной во вторую степень. В применении данной функции в математических моделях проявляется возможность описания и анализа широкого спектра явлений, включая физические, экономические и социологические системы.
Применение функции y = x^2 позволяет моделировать разнообразные процессы, такие как движение тела в пространстве, определение экстремумов функций, распределение ресурсов и многое другое. Зависимость, описываемая этой функцией, отражает квадратичную форму зависимости между переменными и считается одной из основных моделей в математике.
Важно отметить, что функция y = x^2 имеет ряд особенностей, таких как направление отклонения от оси OY, положение вершины параболы и наличие угла отклонения от оси OX. В математических моделях эти особенности позволяют учитывать различные факторы и переменные, которые могут существенно влиять на исследуемую систему.
Анализ возможных проблем и ограничений при использовании функции квадратного уравнения
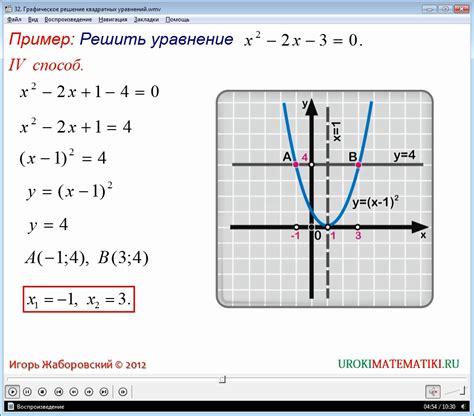
- Ограничение области определения: Не все значения x могут быть использованы в данной функции, поскольку она определена только для вещественных чисел.
- Асимметрия графика: График функции y = x^2 симметричен относительно оси y, но не по отношению к оси x. Это важно учитывать при анализе симметрии и сдвигов в пространстве.
- Единственность корня: Функция имеет только один корень, а именно x = 0. Это ограничение не позволяет полностью удовлетворить требованиям некоторых задач.
- Минимум и максимум: Функция y = x^2 имеет минимум в точке (0, 0) и направлена вверх и вниз бесконечности. Это может вызвать проблемы при определении экстремальных значений в определенных ситуациях.
Таким образом, понимание указанных проблем и ограничений при использовании функции квадратного уравнения позволит более осознанно и эффективно применять ее в различных математических моделях и задачах. Это является важной предпосылкой для достижения точных и надежных результатов при работе с данной функцией.
Вопрос-ответ

Как работает функция y = x^2?
Функция y = x^2 является квадратной функцией, график которой представляет собой параболу. Она строится путем возведения значения x в квадрат и получения соответствующего значения y. Таким образом, каждое значение x имеет свое соответствующее значение y. Например, если x = 2, то y будет равно 4, а если x = -3, то y будет равно 9.
Какие особенности имеет функция y = x^2?
Функция y = x^2 обладает несколькими особенностями. Во-первых, ее график симметричен относительно оси y, что означает, что значения функции симметричны относительно оси y. Во-вторых, функция имеет вершину, которая представляет максимальное или минимальное значение функции. В данном случае, вершина находится в точке (0, 0) и является минимумом, так как функция имеет положительный коэффициент при x^2.
Как изменяется график функции y = x^2 при изменении значения x?
При изменении значения x график функции y = x^2 также изменяется. Если значение x увеличивается, то соответствующее значение y также увеличивается, что приводит к возвышению параболы. Если значение x уменьшается, то y уменьшается, что приводит к опусканию параболы. Все точки параболы симметричны относительно оси y, поэтому изменение значения x в одну сторону влияет на значение y в противоположную сторону от вершины параболы.
Что происходит с графиком функции y = x^2 при изменении коэффициента при x^2?
Изменение коэффициента при x^2 в функции y = x^2 влияет на форму и положение графика. Если коэффициент отрицательный, то график отражается относительно оси x и его ветви направлены вниз. Если коэффициент положительный, то график остается неизменным и его ветви направлены вверх. Коэффициент также определяет, насколько быстро график меняется: чем больше модуль коэффициента, тем более стремительно изменяется график.
Какая математическая функция описывает график y = x^2?
График функции y = x^2 описывается параболой.



