Геометрия – увлекательный предмет, который поможет вам лучше понять окружающий мир и развить логическое мышление. Восьмиклассники изучают различные геометрические фигуры, одной из которых является прямоугольная трапеция. Эта фигура имеет свои особенности и свойства, которые помогут вам решать разнообразные задачи.
Прямоугольная трапеция – это четырехугольник, у которого одна пара противоположных сторон параллельна, а углы, прилегающие к параллельным сторонам, являются прямыми. Изучение свойств и особенностей прямоугольной трапеции поможет вам легко распознавать эту фигуру и решать задачи, связанные с ней.
В данной статье мы рассмотрим основные понятия о прямоугольной трапеции, методы решения задач, связанных с этой фигурой, а также предоставим примеры задач для самостоятельного решения. Погружайтесь в мир геометрии вместе с нами и открывайте новые грани математики!
Прямоугольная трапеция: основные понятия и задачи по геометрии

Для решения задач по геометрии с прямоугольными трапециями используются различные свойства и формулы. Например, вычисление площади прямоугольной трапеции основывается на формуле: S = ((a+b)/2) * h, где a и b – длины оснований, h – высота трапеции. Также можно находить периметр, диагонали, углы и другие параметры этой фигуры, что позволяет решать разнообразные задачи по геометрии.
Понятие прямоугольной трапеции
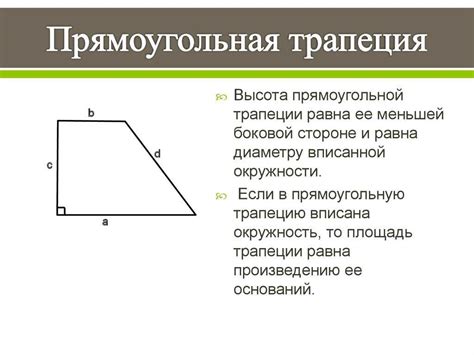
Свойства прямоугольной трапеции
1. Диагонали прямоугольной трапеции
В прямоугольной трапеции диагонали равны между собой и каждая из них делит трапецию на два прямоугольных треугольника.
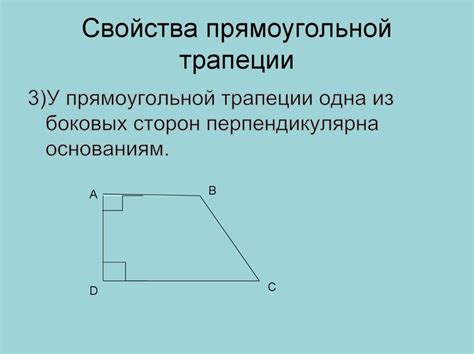
2. Углы прямоугольной трапеции
В прямоугольной трапеции основания параллельны, поэтому углы, образованные диагоналями и боковыми сторонами, равны между собой.
3. Высоты прямоугольной трапеции
Высоты, опущенные из вершин верхнего и нижнего оснований прямоугольной трапеции, равны между собой.
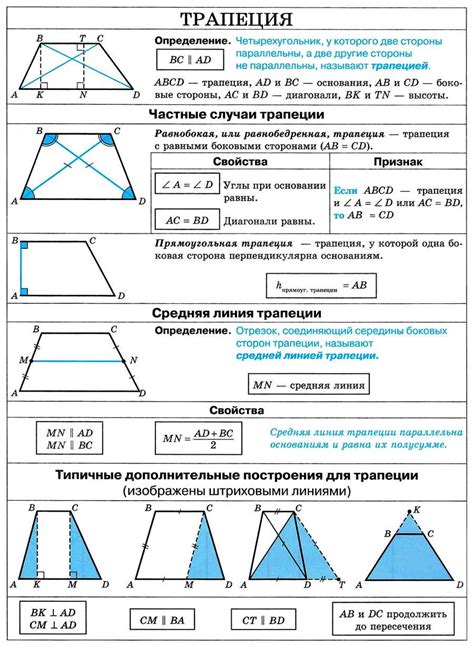
Основные элементы прямоугольной трапеции
- Основания прямоугольной трапеции - это две параллельные стороны, которые образуют прямой угол с боковыми сторонами.
- Боковые стороны - это две стороны прямоугольной трапеции, не являющиеся основаниями, соединяющие соответствующие вершины оснований.
- Высота прямоугольной трапеции - это перпендикуляр из вершины одного основания к другому основанию.
- Средняя линия прямоугольной трапеции - это отрезок, соединяющий середины боковых сторон прямоугольной трапеции.
Формулы для расчетов площади и периметра
Для прямоугольной трапеции можно использовать следующие формулы:
- Площадь прямоугольной трапеции равна полусумме произведений длин оснований на высоту: S = ((a + b) * h) / 2, где a и b – длины оснований, h – высота.
- Периметр прямоугольной трапеции равен сумме всех сторон: P = a + b + c + d, где a, b, c, d – длины всех сторон трапеции.
Эти формулы помогут вам быстро и точно рассчитать площадь и периметр прямоугольной трапеции при решении задач по геометрии.
Задачи на построение прямоугольной трапеции
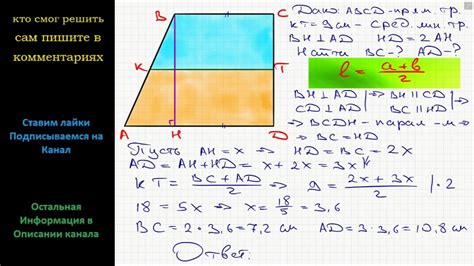
Постройте прямоугольную трапецию ABCD, если AB = 6 см, CD = 10 см, BC = 4 см, AD = 8 см.
Постройте прямоугольную трапецию PQRS, где PQ = 5 см, RS = 9 см, PS = 7 см, QR = 3 см.
Постройте прямоугольную трапецию XYZT, если XT = 12 см, YZ = 5 см, ZX = 8 см, TY = 9 см.
Примеры решения задач с использованием прямоугольной трапеции
1. Задача: В прямоугольной трапеции одно основание равно 6 см, другое основание равно 10 см, а высота равна 4 см. Найдите площадь трапеции.
Решение: Площадь прямоугольной трапеции вычисляется по формуле: S = (сумма оснований * высота) / 2. Подставляем известные значения: S = ((6+10) * 4) / 2 = (16 * 4) / 2 = 64 / 2 = 32 см².
Ответ: Площадь прямоугольной трапеции равна 32 см².
2. Задача: В прямоугольной трапеции длина одного основания равна 12 см, а площадь равна 60 см². Найдите высоту трапеции.
Решение: Площадь прямоугольной трапеции вычисляется по формуле: S = (сумма оснований * высота) / 2. Подставляем известные значения: 60 = (12 + х) * х / 2, где х - высота. Решая уравнение, получаем x² + 12x - 120 = 0. Решив квадратное уравнение, получаем два корня: х₁ = 8, х₂ = -15 (отрицательный корень не подходит).
Ответ: Высота прямоугольной трапеции равна 8 см.
Вопрос-ответ

Что такое прямоугольная трапеция?
Прямоугольная трапеция - это четырехугольник с двумя параллельными сторонами, одна из которых короче другой, и с углами, прилегающими к основаниям, в сумме дающими 180 градусов. В такой трапеции два противоположных угла прямые.
Как найти площадь прямоугольной трапеции?
Чтобы найти площадь прямоугольной трапеции, нужно сложить длины ее оснований, умножить результат на высоту трапеции и разделить на 2. Формула: S = (a + b) * h / 2, где a и b - длины оснований, h - высота.
Как доказать, что данный четырехугольник - прямоугольная трапеция?
Чтобы доказать, что четырехугольник - прямоугольная трапеция, необходимо убедиться, что он имеет две параллельные стороны, одна из которых короче другой, и что сумма углов при основаниях равна 180 градусов.
Какие задачи по геометрии можно решать с использованием прямоугольных трапеций?
С использованием прямоугольных трапеций можно решать задачи на нахождение площади фигуры, нахождение периметра, определение углов, нахождение длины сторон и высоты фигуры, а также задачи на построение различных фигур.
Как связаны диагонали прямоугольной трапеции?
В прямоугольной трапеции диагонали пересекаются в одной точке, которая является их центром пересечения. Диагонали прямоугольной трапеции не равны, их длины могут быть вычислены с использованием теоремы Пифагора.



