Скорость – один из важнейших показателей движения тела, который характеризует изменение положения объекта за определенное время. Равноускоренное движение – это движение тела, при котором его скорость изменяется равномерно. Важно уметь вычислять скорость в равноускоренном движении, так как это позволяет прогнозировать положение и перемещение объекта в будущем.
Для расчета скорости тела в равноускоренном движении используется специальная формула, которая позволяет точно определить этот параметр. Формула для вычисления скорости в равноускоренном движении имеет простой вид: v = v0 + at, где v – конечная скорость, v0 – начальная скорость, a – ускорение и t – время движения.
Для лучшего понимания данной формулы и применения ее на практике рассмотрим конкретный пример расчета скорости в равноускоренном движении. Пусть тело начинает движение с нулевой скоростью (v0 = 0), ускорение равно 2 м/с^2 (a = 2) и время движения составляет 3 секунды (t = 3). Подставив данные в формулу, получим: v = 0 + 2*3 = 6 м/с.
Определение равноускоренного движения

Примеры равноускоренного движения: свободное падение тела под действием силы тяжести, движение тела по наклонной плоскости без трения и другие.
Формула расчета скорости в равноускоренном движении

В равноускоренном движении скорость тела меняется равномерно от момента к моменту. Для расчета скорости в равноускоренном движении можно использовать следующую формулу:
$$v = v_0 + at$$
Где:
- $$v$$ - конечная скорость тела;
- $$v_0$$ - начальная скорость тела;
- $$a$$ - ускорение;
- $$t$$ - время.
Эта формула позволяет определить скорость тела в любой момент времени в равноускоренном движении. Начальная скорость, ускорение и время являются известными величинами, в то время как конечная скорость будет результатом расчета.
Пример расчета скорости в начальный момент времени
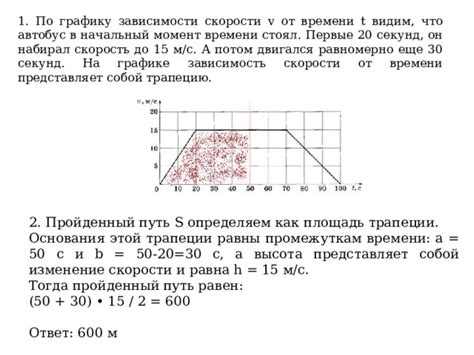
Для тела, находящегося в равноускоренном движении, скорость в начальный момент времени (V0) можно рассчитать, используя формулу:
| Формула: | V0 = V - at |
|---|---|
| Где: | V - конечная скорость тела, a - ускорение тела, t - время движения. |
Например, если тело движется с ускорением 2 м/с² и через 3 секунды его скорость составляет 10 м/с, то можно рассчитать начальную скорость:
| Дано: | Конечная скорость (V) = 10 м/с, Ускорение (a) = 2 м/с², Время движения (t) = 3 с. |
|---|---|
| Решение: | V0 = V - at = 10 - 2*3 = 10 - 6 = 4 м/с |
Пример расчета пути при равноускоренном движении
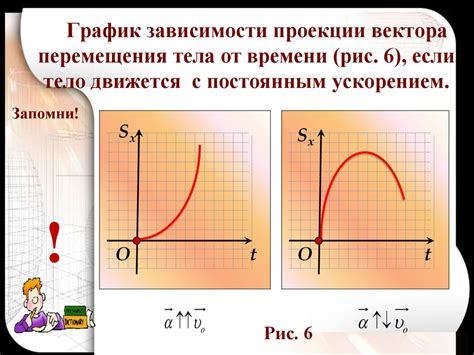
Рассмотрим пример: тело двигается равноускоренно со скоростью 2 м/c². Начальная скорость тела равна 0 м/c, ускорение также составляет 2 м/c². Найдем путь, который тело пройдет за время t = 5 с.
Используем формулу пути в равноускоренном движении: S = v0*t + (a*t^2)/2, где S - путь, v0 - начальная скорость, a - ускорение, t - время.
Подставляем известные значения: v0 = 0 м/c, a = 2 м/c², t = 5 с.
Теперь расчитаем путь: S = 0*5 + (2*5^2)/2 = 0 + 50/2 = 25 м.
Таким образом, тело пройдет 25 м за 5 с при равноускоренном движении.
Важность уравнений равноускоренного движения в физике

Одним из ключевых уравнений равноускоренного движения является формула для вычисления скорости тела в зависимости от времени: v = v₀ + at, где v - скорость тела в конечный момент времени, v₀ - начальная скорость тела, a - ускорение, t - время движения.
Эти уравнения помогают ученым прогнозировать и анализировать движение объектов, как в пространстве, так и на земной поверхности. Благодаря уравнениям равноускоренного движения физики могут предсказать траекторию и скорость движения различных объектов в различных условиях.
Вопрос-ответ

Какая формула позволяет рассчитать скорость тела в равноускоренном движении?
Скорость тела в равноускоренном движении можно найти по формуле: \( v = v_0 + at \), где \( v \) - конечная скорость, \( v_0 \) - начальная скорость, \( a \) - ускорение, \( t \) - время.
Как рассчитать скорость тела в равноускоренном движении, если даны начальная скорость 10 м/c, ускорение 2 м/c² и время 3 секунды?
Для рассчета скорости тела в равноускоренном движении с начальной скоростью 10 м/c, ускорением 2 м/c² и временем 3 секунды используем формулу \( v = 10 + 2 \times 3 = 10 + 6 = 16 \) м/c. Таким образом, скорость тела в данном случае будет 16 м/с.



