Измерение расстояний является важной составляющей в различных областях науки, инженерии и строительства. Высота треугольника с прямым углом – одна из таких величин, которая позволяет точно определить расстояние между горизонтальным и вертикальным отрезками этого треугольника. Одним из способов вычисления высоты является использование тангенса – одного из тригонометрических соотношений.
Тангенс – это отношение противоположной стороны треугольника к прилежащей стороне. В случае треугольника с прямым углом, противоположная сторона соответствует ему высоте, а прилежащая – основанию треугольника. Следовательно, нахождение высоты треугольника с прямым углом может быть сведено к определению тангенса угла между основанием и горизонтальной плоскостью.
Для решения данной задачи вам понадобятся значения длины основания и угла между основанием и горизонтальной плоскостью. С помощью тригонометрического соотношения тангенса вы сможете найти значения противоположной стороны – высоты треугольника. Этот метод особенно полезен в сферах инженерии и архитектуры, где точное определение высоты является неотъемлемой частью процесса планирования и строительства.
Особенности прямоугольного треугольника

В прямоугольном треугольнике можно выделить три стороны: гипотенузу – самую длинную сторону, и две катеты – более короткие стороны, которые образуют прямой угол. Гипотенуза и катеты могут быть разной длины, но всегда сохраняется соотношение, известное как теорема Пифагора: квадрат длины гипотенузы равен сумме квадратов длин катетов.
Прямоугольные треугольники широко используются в различных областях, включая геодезию, физику, астрономию, строительство и многие другие. Знание особенностей и свойств прямоугольного треугольника позволяет решать задачи на вычисление его сторон, площади и высоты с помощью различных математических формул и тригонометрических функций, таких как тангенс, синус и косинус.
- Прямоугольный треугольник – геометрическая фигура с одним прямым углом;
- Теорема Пифагора – соотношение между длинами гипотенузы и катетов;
- Применение в различных областях науки и инженерии;
- Вычисление сторон, площади и высоты с использованием математических формул.
Высота прямоугольного треугольника и ее значение через тангенс
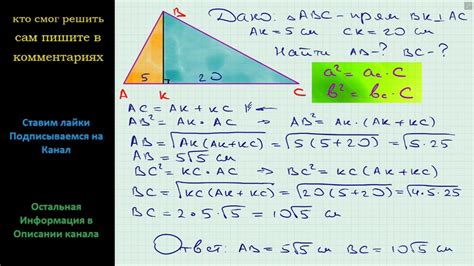
В изучении геометрии прямоугольных треугольников, знание высоты этой фигуры через тангенс играет важную роль. Понимание значения высоты позволяет определить длину этого отрезка, который соединяет вершину прямого угла с противолежащей стороной, а также его влияние на свойства и применение этого треугольника.
Существует несколько причин, по которым знание высоты прямоугольного треугольника через тангенс является полезным. Во-первых, это дает возможность точно вычислить длину стороны треугольника, которая не является гипотенузой или катетом. Это особенно полезно при решении задач, связанных с конструкцией или измерением без доступа к специальным инструментам.
Знание высоты прямоугольного треугольника через тангенс также позволяет рассмотреть его геометрические свойства. Одним из примеров является использование таких треугольников в архитектуре и строительстве. Зная высоту через тангенс, можно определить оптимальные углы наклона и расстояние между плоскостями, что существенно влияет на структурную прочность и эстетическое восприятие.
Важным применением знания высоты прямоугольного треугольника через тангенс является его использование в тригонометрии и математике. Решение задач и уравнений, связанных с треугольниками, может потребовать нахождения высоты через данную тригонометрическую функцию. Понимание этой концепции поможет провести вычисления и получить точные результаты.
- Вычисление длин сторон треугольника, не являющихся гипотенузой или катетом.
- Использование в архитектуре и строительстве для определения углов наклона и расстояний.
- Применение в тригонометрии и математике для решения задач и уравнений.
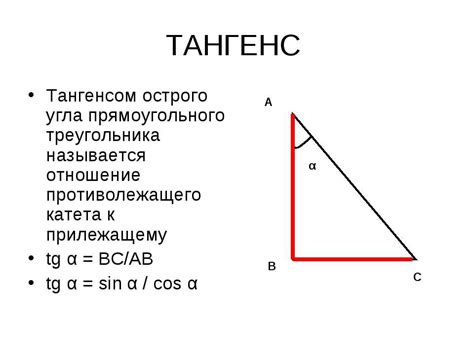
Определение тангенса
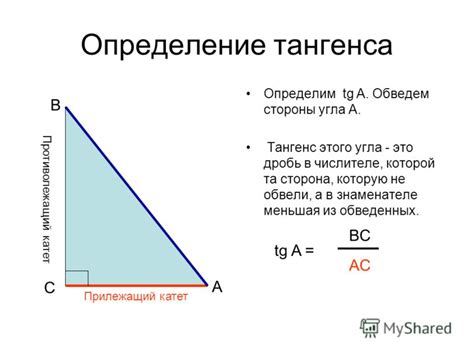
Тангенс выражает отношение длины противоположего катета к длине прилежащего катета в прямоугольном треугольнике, а также отношение координат точки на окружности, которая является синусом данного угла и будучи нормированной делением на длину радиуса окружности, к координате проекции этой точки на горизонтальную ось. Тангенс обозначается как tan или tg.
Пример использования:
Рассмотрим прямоугольный треугольник со сторонами a, b и гипотенузой c. Тогда тангенс угла α можно вычислить как tg(α) = a/b.
Интересный факт: В физике и инженерии тангенс широко используется для расчетов механических систем, электрических цепей и других областей, где необходимо определить соотношение между силами или значениями величин.
Определение и вычисление тангенса
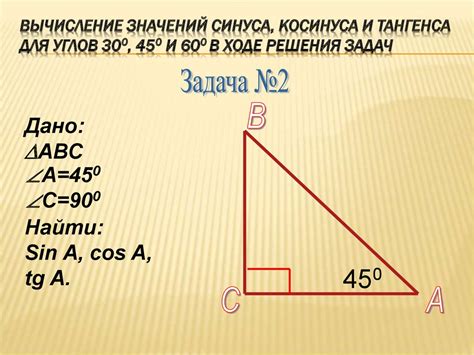
Чтобы вычислить тангенс, можно воспользоваться триметрической формулой, которая устанавливает связь между углом и сторонами треугольника. В этой формуле, тангенс определяется как отношение противоположной стороны к прилежащей стороне:
- Тангенс угла α = противоположная сторона / прилежащая сторона
Для вычисления тангенса необходимо знать значения обоих сторон и подставить их в формулу. Результат будет числовым значением, которое показывает величину тангенса угла треугольника.
Очертания тангенса в геометрии
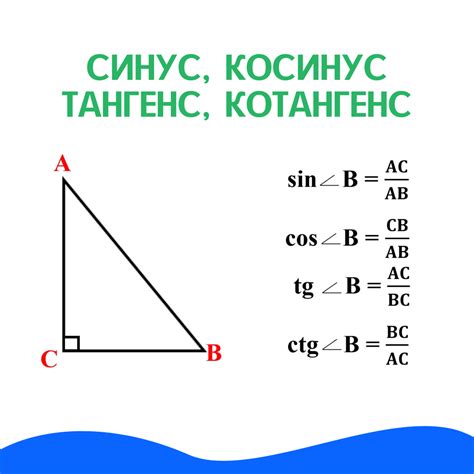
Когда мы говорим о геометрическом смысле тангенса, мы подразумеваем его способность связывать длины сторон треугольника с его углами. Какую-то особую задачу решает именно тангенс, при благоприятных обстоятельствах нам не нужны другие тригонометрические функции, и мы можем получить все необходимые данные из него.
Тангенс позволяет нам определить отношение длины противоположной катеты к длине прилежащего катеты в прямоугольном треугольнике. Это отношение является важным ключом в анализе и решении геометрических задач, так как оно помогает нам вычислить длины сторон треугольника или определить его форму.
Связь между тангенсом и высотой прямоугольного треугольника
Используя определение тангенса и связь его со сторонами треугольника, мы можем вывести формулу, позволяющую найти высоту треугольника через тангенс. Для этого необходимо знать длины сторон, взаимно противоположных катетов, а также знать значение тангенса одного из углов.
Одним из способов применения формулы является нахождение высоты прямоугольного треугольника при известных значениях сторон и/или углов. В результате применения формулы мы получим точное значение высоты треугольника, что может быть полезным при решении задач, связанных с построением, измерениями и вычислениями в геометрии.
Итак, связь между тангенсом и высотой прямоугольного треугольника позволяет нам использовать геометрические и алгебраические методы для определения высоты треугольника без знания других параметров. Благодаря этой связи мы можем более точно и эффективно решать задачи, связанные с прямоугольными треугольниками.
- Ознакомьтесь с определением тангенса и его связью со сторонами треугольника.
- Выведите формулу для нахождения высоты прямоугольного треугольника через тангенс.
- Примените формулу для решения задачи нахождения высоты при известных значениях углов или сторон.
Как применять тангенс для определения высоты треугольника?

Для вычисления высоты прямоугольного треугольника с использованием тангенса необходимо знать длины двух его сторон. Сначала определяется значение тангенса угла между одним из катетов и гипотенузой. Затем, зная длину одного из катетов и значение тангенса, можно рассчитать длину противолежащего катета. Это значение представляет собой искомую высоту треугольника.
Для использования данного метода достаточно знать значения двух известных величин - длины катета и угла между этим катетом и гипотенузой. Зная эти данные, можно легко определить высоту треугольника через применение тангенса и проведение простых вычислений.
Какие данные нужны для вычисления вертикальной линии?

Примеры вычислений

В данном разделе приведены практические примеры расчета высоты прямоугольного треугольника с использованием тангенса. Предлагаем ознакомиться с несколькими примерами, которые помогут лучше понять методику расчета.
- Пример 1:
- Пример 2:
- Пример 3:
Предположим, у нас есть прямоугольный треугольник с основанием 8 см и углом α. Чтобы вычислить высоту треугольника, опирающуюся на данную сторону, мы можем воспользоваться теоремой тангенсов.
Для этого нужно найти тангенс угла α. Подставим значения основания и высоты в формулу тангенса: тангенс α = высота / основание.
Теперь мы можем решить уравнение относительно высоты и найти ее значение.
Допустим, у нас есть треугольник, у которого известна высота 12 см и угол β. Чтобы найти основание треугольника, мы также будем использовать формулу тангенса.
Сначала найдем тангенс угла β, подставив значения высоты и основания в формулу: тангенс β = высота / основание.
Затем решим уравнение относительно основания и найдем его значение.
Представим ситуацию, когда известно основание треугольника и угол γ. Чтобы вычислить высоту треугольника, мы, естественно, воспользуемся формулой тангенса.
Подставим значения основания и высоты в формулу тангенса: тангенс γ = высота / основание.
Решим уравнение относительно высоты и найдем ее значение.
Это лишь несколько примеров расчета высоты прямоугольного треугольника через тангенс. Учитывая данные и используя формулу тангенса, можно находить высоту при различных известных величинах треугольника.
Пример 1: Расчет высоты прямоугольного треугольника с использованием тангенса
Для начала, нам необходимо знать значение одного из углов треугольника. Давайте обозначим его как α. С помощью тангенса этого угла, мы можем определить отношение противоположной стороны (высоты) к прилежащей стороне (основанию треугольника):
| Формула: | tan(α) = высота / основание |
| Высота | = tan(α) * основание |
Теперь, зная значение угла α и длину основания треугольника, мы можем рассчитать высоту треугольника, используя формулу tan(α) * основание. Этот метод позволяет нам определить высоту прямоугольного треугольника с использованием тангенса.
Пример 2: Расчет высоты при заданных значениях углов и сторон треугольника
Давайте рассмотрим пример вычисления высоты прямоугольного треугольника, при котором заданы значения углов и сторон треугольника. Этот метод позволит нам определить высоту треугольника с использованием различных входных данных, что может быть полезно при решении геометрических задач и нахождении неизвестных параметров.
Вопрос-ответ

Как найти высоту прямоугольного треугольника через тангенс?
Для того чтобы найти высоту прямоугольного треугольника через тангенс, необходимо знать значение одного из углов треугольника и длину одного из катетов. Воспользуйтесь формулой: высота = катет * tg(угол).
Какое значение угла нужно знать, чтобы использовать формулу для нахождения высоты прямоугольного треугольника через тангенс?
Для использования формулы нужно знать значение одного из острых углов треугольника. Согласно теореме Пифагора, сумма всех углов прямоугольного треугольника равна 180 градусов, поэтому второй острый угол можно вычислить, зная значение первого острого угла.
Можно ли использовать формулу для нахождения высоты прямоугольного треугольника через тангенс, если известны лишь длины катетов?
Нет, для использования этой формулы нужно знать значение одного из углов треугольника. Если известны только длины катетов, можно воспользоваться формулой Пифагора для нахождения гипотенузы треугольника, а затем применить другую формулу для высоты.



