Отрицательные корни уравнения могут быть источником сложности и неопределенности при решении математических задач. Однако, есть методы, которые помогают доказать, что уравнение не имеет отрицательных корней. В данной статье мы рассмотрим один из таких методов.
Предположим, что уравнение вида ax^2 + bx + c = 0, где a, b и c - действительные числа, не имеет отрицательных корней. Для доказательства этого утверждения, рассмотрим дискриминант уравнения D = b^2 - 4ac. Если D
Таким образом, доказать отсутствие отрицательных корней уравнения можно путем анализа его дискриминанта. Этот метод является надежным и позволяет с легкостью определить характер корней уравнения, что может быть полезно при решении математических задач различной сложности.
Уравнение и его природа

Изучение корней уравнения

Для изучения корней уравнения сначала необходимо определить коэффициенты в уравнении. После этого можно применить различные методы решения уравнения, такие как метод дискриминанта или метод подстановки.
Важно также проверить возможное наличие отрицательных корней уравнения. Для этого необходимо рассмотреть дискриминант уравнения и определить его значение. Если дискриминант положителен, то у уравнения будут два вещественных корня. В случае отрицательного дискриминанта, уравнение не будет иметь вещественных корней, но возможно будут комплексные.
Доказательство отсутствия отрицательных корней
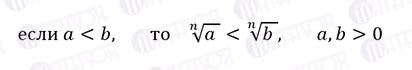
Для доказательства отсутствия отрицательных корней уравнения, достаточно использовать теорему о неравенстве арифметического и геометрического средних.
Предположим, что уравнение имеет отрицательный корень. Тогда сумма корней уравнения будет равна отрицательному коэффициенту при x в уравнении второй степени. Но согласно теореме об арифметическом и геометрическом средних, арифметическое среднее всегда больше или равно геометрическому.
Таким образом, если уравнение имеет отрицательный корень, то сумма корней будет меньше, чем арифметическое среднее корней. Это противоречие показывает, что уравнение не может иметь отрицательных корней.
Метод анализа уравнений

Для доказательства отсутствия отрицательных корней уравнения можно использовать метод анализа.
- Шаг 1: Начните с выражения уравнения в стандартной форме.
- Шаг 2: Исследуйте коэффициенты уравнения, чтобы определить возможные значения корней.
- Шаг 3: Проанализируйте знаки коэффициентов и свойства уравнения для проверки наличия отрицательных корней.
Проведя тщательный анализ, можно убедиться в отсутствии отрицательных корней и завершить доказательство утверждения.
Утверждение и его подтверждение

Вопрос-ответ

Почему отсутствуют отрицательные корни уравнения?
Отсутствие отрицательных корней уравнения можно доказать, если уравнение представлено в квадратном виде с положительным коэффициентом при старшей степени. При этом отрицательные корни уравнения не существуют, так как их не может быть при положительных коэффициентах. Также можно использовать методы анализа графиков функций для подтверждения отсутствия отрицательных корней.
Как можно убедиться, что уравнение не имеет отрицательных корней?
Для доказательства отсутствия отрицательных корней уравнения необходимо проанализировать коэффициенты при его переменных. Если все коэффициенты уравнения положительны, то это говорит о том, что отрицательных корней у уравнения нет. Также можно воспользоваться методом исследования знаков функций или построением графика функции для подтверждения отсутствия отрицательных корней.



