Несомненно, одним из фундаментальных понятий геометрии является параллельность прямых. Во многих задачах и теоремах требуется доказать, что две или три прямые являются параллельными. Однако, такое доказательство требует аккуратной и последовательной логики.
Существуют различные методы и подходы для доказательства параллельности прямых. Один из них основан на использовании аксиом и свойств параллельных линий, в то время как другой базируется на использовании особенностей углов и отношений между прямыми. В обоих методах необходимо явное и логическое обоснование каждого шага доказательства.
Для лучшего понимания доказательства параллельности прямых необходимо рассмотреть реальные примеры и конкретные ситуации. Такие примеры помогут нам визуализировать абстрактные понятия и обеспечат более глубокое осознание принципов и методов доказательства параллельности прямых.
Варианты подтверждения параллельности двух прямых
В данном разделе приведены методы, позволяющие установить факт параллельности двух прямых. Рассмотрим различные подходы и приемы, характеризующие эту важную геометрическую характеристику.
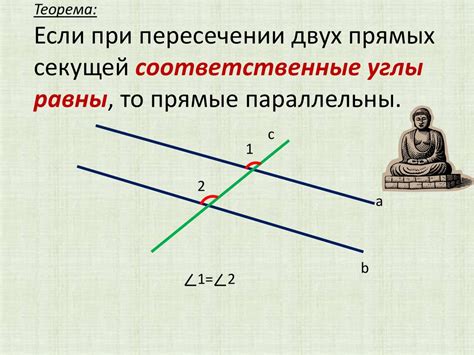
Первым из рассматриваемых методов является использование свойства равенства соответствующих углов. Данное правило позволяет установить параллельность двух прямых путем сравнения величин углов, образованных при пересечении с третьей прямой или с прямой-трансверсалью. Достоверность данного метода основывается на аксиоме о равенстве углов двух параллельных прямых.
Второй метод связан с применением свойства пропорциональности отрезков, образованных пересечением параллельных прямых третьей прямой или лучом. Используя соотношение отрезков, удается выявить параллельность и углы, сформированные пересечением данных прямых.
Еще одним способом подтверждения параллельности является анализ формы и строения геометрических фигур, образованных параллельными прямыми и прямыми-трансверсалями. Этот метод позволяет определить характерный образец, признаком которого является параллельность данных прямых.
Метод углового уравнения: универсальный подход к доказательству параллельности прямых
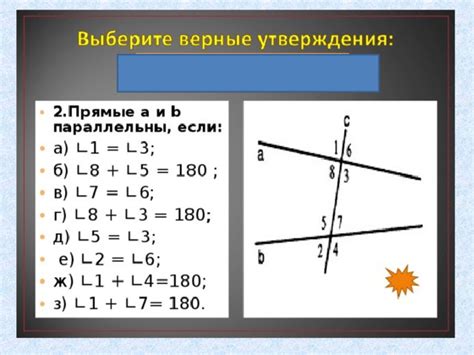
В области геометрии существует метод, позволяющий эффективно и точно определить параллельность двух прямых. Этот метод основан на использовании углового уравнения и может быть применен в различных ситуациях, где требуется доказать, что две прямые расположены параллельно друг другу.
Суть метода заключается в анализе углов, образованных рассматриваемыми прямыми с третьей прямой, называемой трансверсальной. При использовании углового уравнения можно получить информацию о соотношении углов и, следовательно, о параллельности прямых. Важно отметить, что данный подход не ограничивается только двумя прямыми - он также применим к группам прямых в трехмерном пространстве.
Преимущество метода углового уравнения заключается в его универсальности. Он может быть использован для доказательства параллельности в различных геометрических конструкциях, таких как треугольники, параллелограммы, пересекающиеся прямые и многое другое. Этот метод позволяет существенно сократить время и усилия, затрачиваемые на доказательство параллельности, и обеспечивает точные и надежные результаты.
Поэтому метод углового уравнения является мощным инструментом для геометрических исследований, обладающим широким спектром применения и позволяющим обнаружить важные свойства параллельных прямых и их взаимоотношения с другими геометрическими объектами.
Метод сопоставления углов

В этом разделе рассматривается метод определения параллельности двух и трех прямых на основе сравнения углов, которые они образуют.
| Сравнение углов | Описание |
|---|---|
| Углы наклона | Сравниваются углы наклона прямых и определяется, являются ли они равными. |
| Вертикальные углы | Проверяется, являются ли углы между двумя пересекающимися прямыми вертикальными, что говорит о их параллельности. |
| Соответствующие углы | Определяется равенство соответствующих углов при пересечении прямых с трансверсальной линией, что указывает на их параллельность. |
Метод сравнения углов позволяет установить параллельность прямых, исходя из геометрических свойств, связанных с их углами. Этот метод широко применяется при доказательстве параллельности в геометрии и находит свое применение в различных практических ситуациях.
Путь к определению параллельности с помощью метода средней линии пересечения
- Средняя линия пересечения является прямой, проходящей через точки пересечения с другими прямыми.
- Если средняя линия пересечения параллельна третьей прямой, то первоначальные прямые также параллельны.
- Если средняя линия пересечения пересекает третью прямую, то первоначальные прямые не являются параллельными.
Метод средней линии пересечения предоставляет простой и эффективный способ для доказательства параллельности двух прямых посредством анализа их взаимного отношения с третьей прямой. Этот метод может быть очень полезен при решении различных геометрических задач и нахождении точек пересечения прямых.
Использование параллельных линий в геометрии

Один из методов, широко применяемых в геометрии, заключается в использовании параллельных линий. Этот метод позволяет решать различные задачи, связанные с доказательством параллельности и нахождением соотношений между прямыми. Параллельные линии создают основу для построения и анализа различных геометрических фигур, что помогает нам лучше понять и визуализировать пространственные отношения.
1. Параллельные прямые и их свойства Параллельные прямые - это линии, которые никогда не пересекаются и всегда остаются на одинаковом расстоянии друг от друга. Они имеют ряд особенностей и свойств, которые могут быть использованы для анализа и доказательства параллельности в задачах геометрии. | 2. Параллельные линии и углы Параллельные линии образуют углы, которые между собой имеют особую связь. Например, вертикальные углы, образуемые пересекающимися прямыми и их параллельными линиями, равны между собой. Это свойство может быть использовано для доказательств параллельности и нахождения значений углов. |
3. Параллельные линии и треугольники Параллельные линии также взаимодействуют с треугольниками, создавая особенности, которые можно использовать для доказательства или нахождения соотношений между их сторонами и углами. Например, если в треугольнике две стороны параллельны, то его третья сторона будет разрезать две параллельные линии в пропорциональных отношениях. | 4. Применение параллельных линий в решении задач Использование параллельных линий широко применяется при решении задач геометрии. Например, задачи на нахождение периметра или площади фигуры могут быть связаны с использованием параллельных линий и соотношениями между сторонами и углами. Умение использовать этот метод позволяет более эффективно решать геометрические задачи и получать более точные результаты. |
Раздел: Пути установления параллельности трех прямых

Важно отметить, что каждый из этих методов имеет свои сильные стороны и учет их различий может помочь в выборе наиболее эффективного подхода для доказательства параллельности трех прямых в конкретной ситуации. Некоторые методы могут обращаться к конструктивному подходу, где требуется создать дополнительные линии или фигуры, чтобы подтвердить параллельность, в то время как другие методы полагаются на использование уже известных свойств и связей, таких как равенства или соответствие углов.
Определение подходящего метода доказательства требует понимания характеристик и особенностей данных прямых и их взаимоотношений. Это позволяет выбрать оптимальный метод, который приносит наибольшую уверенность в ответе. Для наглядности и более полного понимания рассмотрим конкретные примеры применения различных методов доказательства параллельности трех прямых.
Определение отношения эквидистанты

Для начала, рассмотрим следующую таблицу, где каждой точке сопоставлены ее координаты:
| Точка | Координаты |
|---|---|
| A | (xA, yA) |
| B | (xB, yB) |
| C | (xC, yC) |
| D | (xD, yD) |
Затем, мы вычисляем расстояния между точками AB и CD:
| Расстояние | Значение |
|---|---|
| AB | dAB = √((xA - xB)² + (yA - yB)²) |
| CD | dCD = √((xC - xD)² + (yC - yD)²) |
Сравнение угловых коэффициентов: метод понимания параллельности прямых
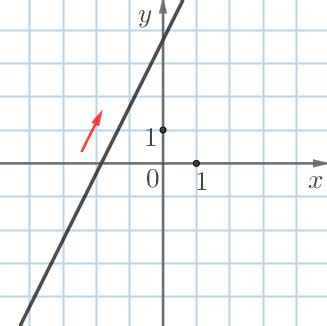
Преимущества метода сравнения угловых коэффициентов:
В данном методе не требуется использование сложных математических конструкций и формул, что делает его более доступным и понятным для начинающих. Сравнение угловых коэффициентов позволяет быстро определить параллельность двух прямых на основе их визуального наклона и представления на плоскости.
Важно отметить, что сравнение угловых коэффициентов затруднено в случае вертикальных и горизонтальных прямых, так как у них угловые коэффициенты равны бесконечности и нулю соответственно. В таких случаях необходимо использовать другие методы для доказательства параллельности.
Ниже представлен пример использования метода сравнения угловых коэффициентов:
Предположим, у нас есть две прямые с угловыми коэффициентами k1 = 2 и k2 = 2. Если угловые коэффициенты двух прямых равны, это указывает на параллельность между ними. В данном случае, прямые параллельны друг другу.
Метод нахождения средней линии пересечения плоскостей
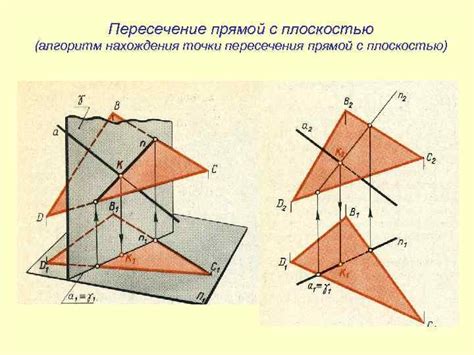
В данном разделе будет рассмотрен метод определения средней линии пересечения плоскостей. Этот метод позволяет найти общую линию, по которой пересекаются две или более плоскости, и определить их параллельность.
Суть метода заключается в том, что для нахождения средней линии пересечения плоскостей необходимо определить их направляющие векторы и соотношения между ними. Путем анализа этих соотношений можно установить, что плоскости параллельны или пересекаются.
Применение метода средней линии пересечения плоскостей может быть полезным при решении геометрических и физических задач, в которых требуется определить параллельность плоскостей или найти точку их пересечения.
| Пример | Плоскости | Направляющие векторы | Соотношение | Результат |
|---|---|---|---|---|
| Пример 1 | Плоскость A | Вектор a1 | Перпендикулярно | Пересекаются |
| Пример 2 | Плоскость B | Вектор b1 | Коллинеарно | Параллельны |
| Пример 3 | Плоскости C и D | Вектор c1, вектор d1 | Неколлинеарны | Пересекаются |
Таким образом, метод средней линии пересечения плоскостей предоставляет возможность определить параллельность двух или более плоскостей, используя их направляющие векторы и анализируя соотношения между ними. Знание этого метода может быть полезным при решении различных задач, связанных с параллельностью и пересечением плоскостей.
Вопрос-ответ

Как доказать параллельность двух прямых?
Для доказательства параллельности двух прямых необходимо проверить выполнение одного из следующих условий: 1. Углы, образованные данными прямыми и пересекающимися прямыми, равны; 2. Расстояние между данными прямыми постоянно; 3. Прямые имеют одно и то же направление.
Какой метод используется для доказательства параллельности трех прямых?
Для доказательства параллельности трех прямых можно использовать метод сравнения углов, образованных этими прямыми и пересекающими прямыми. Если углы при основании равны, то прямые параллельны.
Какие бывают примеры параллельных прямых?
Примерами параллельных прямых могут быть: 1. Две горизонтальные прямые, например, линия горизонта и горизонтальная линия на плоскости; 2. Две вертикальные прямые, например, стоящие рядом столбы; 3. Две наклонные параллельные прямые, например, две дороги, которые идут параллельно друг другу.
Можно ли использовать метод расстояний для доказательства параллельности прямых?
Да, можно использовать метод расстояний для доказательства параллельности прямых. Если расстояние между двумя прямыми постоянно, то они параллельны. Для этого можно провести перпендикуляр от одной прямой к другой и измерить расстояние между ними.
Какие еще методы можно использовать для доказательства параллельности прямых?
Помимо метода углов и метода расстояний, для доказательства параллельности прямых можно использовать метод сравнения коэффициентов наклона. Если у двух прямых коэффициенты наклона равны, то они параллельны.



