Вполне возможно, что геометрия является одним из самых загадочных разделов математики. Ее магия и притягательность могут увлечь любого, кто осмысленно проникает в мир фигур и пространств. Одной из самых интересных и сложных задач геометрии является определение высоты равнобедренного треугольника. Эта увлекательная задача требует внимательности и математической сообразительности, а также знания специфических формул и закономерностей. В данной статье мы расскажем вам о секретах геометрии, связанных с вычислением высоты равнобедренного треугольника.
Если вам кажется, что геометрия - это скучное и неприметное занятие, то вы глубоко заблуждаетесь. Раздел, который является крошечной частицей математики, геометрия оказывает воздействие на многие сферы нашей жизни - архитектуру, строительство, дизайн, астрономию и даже искусство. Попытка разгадать ее тайны и ознакомиться с ее законами становится все более важной в современном мире.
Один из самых увлекательных элементов геометрии - равнобедренный треугольник. Своими симметричными и пропорциональными сторонами он привлекает внимание учеников и студентов со школьной скамьи и до университетской аудитории. Особенно интересной задачей, связанной с равнобедренным треугольником, является определение его высоты - грандиозной формулы. Но не стоит пугаться, ведь с нашими подробными объяснениями и уникальными способами вычислений вы сможете успешно разгадать эту загадку геометрии.
Математическая формула для определения высоты равнобедренного треугольника
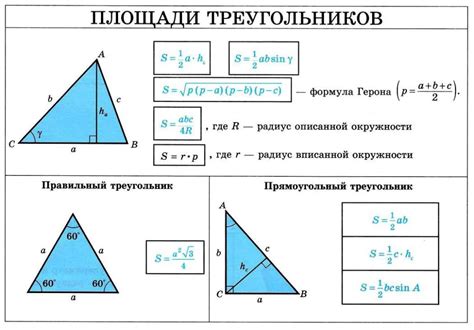
Этот раздел посвящен математической формуле, позволяющей вычислить высоту равнобедренного треугольника. Несмотря на то, что вычисление высоты треугольника может показаться сложной задачей, использование данной формулы делает процесс более простым и понятным.
Эта формула основана на особенностях равнобедренного треугольника. Равнобедренный треугольник имеет две равные стороны и два равных угла, что позволяет нам использовать определенные свойства для вычисления его высоты.
- Шаг 1: Найдите длину основания – это одна из равных сторон треугольника.
- Шаг 2: Найдите половину основания и обозначьте его как А.
- Шаг 3: Используя формулу, находим высоту треугольника, подставляя длину основания и половину основания в нужные переменные.
Применение данной формулы позволяет определить высоту равнобедренного треугольника без особых сложностей, учитывая его особенности и свойства. Зная длину основания, мы можем легко вычислить высоту и использовать эту информацию для решения различных задач и проблем, связанных с равнобедренными треугольниками.
Основы геометрии и их практическое применение

Одним из главных принципов геометрии является изучение геометрических фигур и их элементов, таких как точки, линии, углы, отрезки и плоскости. Знание основных свойств этих элементов позволяет решать сложные задачи, например, построение перпендикуляров или нахождение середин отрезка.
Еще одним важным принципом геометрии является применение теорем и формул для вычисления различных параметров фигур. Например, с помощью формулы площади можно найти площадь треугольника, прямоугольника или окружности. Теорема Пифагора позволяет находить длину сторон треугольника, а теорема косинусов и синусов - находить углы в треугольнике.
Также принципы геометрии применяются в различных областях, таких как строительство и архитектура. Знание и умение применять геометрические принципы позволяет строить прочные сооружения, располагать отверстия в стенах или решать проблемы симметричной компоновки элементов интерьера.
В итоге, понимание основных принципов геометрии и их применение в практической жизни помогает решать сложные задачи и анализировать пространственное расположение объектов. Умение работать с геометрическими фигурами и использовать формулы и теоремы позволяет нам оперативно решать множество задач и достигать желаемых результатов.
Исследование высоты равнобедренного треугольника: тайны изучения геометрических фигур
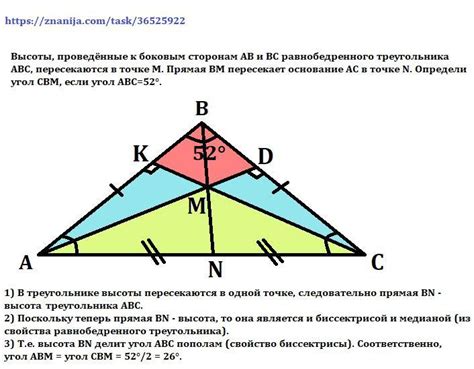
В этом разделе мы рассмотрим интересные аспекты вычисления высоты равнобедренного треугольника и погрузимся в мир геометрии, для того чтобы обнаружить скрытые закономерности и секреты этой фигуры.
Мы рассмотрим способы определения высоты равнобедренного треугольника без использования прямых формул и вычислений. Будут исследованы связи между сторонами и углами треугольника, а также рассмотрены особенности этой фигуры в контексте ее использования в различных областях, таких как архитектура, инженерия и графика.
Мы также рассмотрим вариации равнобедренных треугольников и их особенности, что позволит углубиться в изучение геометрии и понять, как эта фигура играет важную роль в различных математических и научных задачах.
Ключевые этапы в вычислении и понимании геометрической формулы: обзор общих принципов

В данном разделе мы познакомимся с важными этапами, которые помогут нам вычислить и осознать геометрическую формулу. Это позволит нам лучше понять и применять ее в практических задачах без необходимости обращаться к подробным определениям.
- Изучение фундаментальных концепций: на первом этапе необходимо усвоить базовые понятия геометрии, такие как углы, стороны, вершины, отрезки и т.д. Это создаст основу для правильного понимания и использования формулы.
- Применение правил для конкретного случая: на втором этапе мы будем применять правила и теоремы, которые связаны с геометрической формулой. Это поможет нам вывести необходимые шаги для решения задачи и получения точного результата.
- Исследование различных примеров: чтобы лучше понять и усвоить формулу, важно рассмотреть несколько конкретных примеров, которые иллюстрируют применение формулы на практике. Это поможет нам уловить общий смысл и особенности вычислений.
- Анализ возможных ошибок и их устранение: на четвертом этапе мы рассмотрим распространенные ошибки, которые могут возникнуть при вычислении и применении геометрической формулы. Благодаря этому анализу мы сможем избегать неправильных решений и повысить точность вычислений.
Помните, что понимание геометрической формулы важно для применения ее в реальных ситуациях. Следуя данным ключевым этапам, вы сможете не только вычислить высоту равнобедренного треугольника, но и обрести более глубокое понимание геометрии в целом.
Вопрос-ответ

Какая формула позволяет вычислить высоту равнобедренного треугольника?
Для вычисления высоты равнобедренного треугольника можно использовать формулу, которая основана на свойствах этого треугольника. Высота равнобедренного треугольника может быть найдена по формуле: h = √(a^2 - (b/2)^2), где h - высота, a - длина основания, b - длина боковой стороны.
Какие свойства равнобедренного треугольника используются при вычислении его высоты?
При вычислении высоты равнобедренного треугольника используются свойства этого треугольника. Один из основных принципов заключается в том, что высота является перпендикуляром к основанию треугольника и делит его пополам. Это позволяет использовать формулу, с помощью которой можно вычислить высоту равнобедренного треугольника.
Каким образом можно применить формулу для вычисления высоты равнобедренного треугольника на практике?
Формула для вычисления высоты равнобедренного треугольника может быть полезна во многих практических ситуациях. Например, если известны длина основания и длина одной из боковых сторон, можно легко вычислить высоту треугольника. Такая информация может пригодиться при строительстве или проектировании различных конструкций, а также при решении геометрических задач в школьном курсе математики.



