Числа - это загадочная сущность, окутанная тайнами и потаенными свойствами. Увлекательное приключение начинается, когда мы пытаемся разгадать их секреты и раскрыть истину, скрытую за цифровыми комбинациями. Во вселенной программирования, Python - непревзойденный инструмент для исследования и манипулирования числами.
И хотя не существует универсальной "клавиши знания", которая сразу же раскрывает все тайны числовой магии, в этой статье мы сфокусируемся на одном из самых увлекательных аспектов: поиске корней третьей степени. Ради того, чтобы наше путешествие было по-настоящему разнообразным и интересным, мы рассмотрим каждый шаг этого процесса, разобьем его на маленькие фрагменты, и даже познакомимся с некоторыми полезными примерами.
Подготовьтесь отправиться в увлекательное путешествие в мир чисел, где мы применим свои знания Python и развернем комбинаторный венец на голове численных загадок. Готовы ли вы отправиться в опасное и увлекательное путешествие? Тогда давайте начнем исследование корней третьей степени и раскроем тайны численных связей, которые скрыты в цифровой вселенной.
Что такое третий квадратный корень и его значение
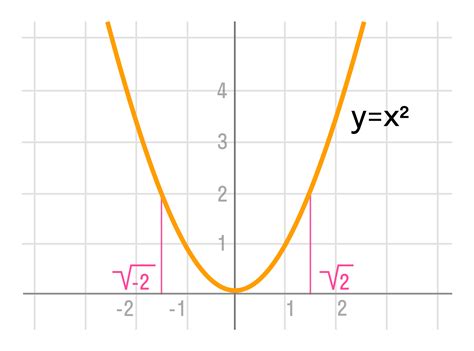
В данном разделе мы рассмотрим понятие третьего квадратного корня и значимость его значения в математике. Третий квадратный корень представляет собой число, которое, умноженное на себя три раза подряд, даёт исходное число. Этот математический оператор позволяет находить одну из трёх возможных корней, которые могут быть извлечены из числа. Значение третьего квадратного корня имеет широкое применение в физике, инженерии и других науках, где необходимо решать задачи, связанные с объемами, периметрами и площадями.
Для нахождения третьего квадратного корня из числа в языке программирования Python существует несколько способов, однако мы не будем детально рассматривать их в данной статье, поскольку основное внимание будет уделено объяснению сути третьего квадратного корня и его значения. Однако, при желании, можно найти примеры реализации данной операции в литературе или посмотреть видеоуроки, где подробно объясняются различные методы поиска корня третьей степени.
Начнем с примера, чтобы более наглядно представить, как третий квадратный корень отличается от квадратного корня. Представим, что данное число 27. Третий квадратный корень из 27 будет равен 3, так как число 3 умноженное на себя три раза даёт исходное число 27. Если бы мы искали квадратный корень из 27, то найденным значением было бы 5.196, так как число 5.196, возведенное в квадрат, даёт исходное число 27.
Таким образом, значения третьего квадратного корня являются рациональными числами и позволяют решать разнообразные задачи в математике и науке в целом. В следующих разделах мы рассмотрим более подробно применение третьего квадратного корня и его свойства, которые сделают понятие корня третьей степени еще более полным и интересным для изучения.
Роль нахождения кубического корня числа в программировании на Python

Нахождение кубического корня из числа позволяет получить такую величину, что при возведении ее в куб будет получено исходное число. Эта операция может быть полезна при извлечении объема кубического объекта по его размерам или при нахождении стороны куба по его объему. Также, нахождение кубического корня может быть полезным при оценке сложности задачи или исследовании изменения какой-либо величины в трехмерном пространстве.
В программировании на языке Python, нахождение кубического корня числа может быть выполнено с помощью различных методов и алгоритмов. Один из самых простых и понятных способов - использование оператора возвода в степень и корневого извлечения. Также, существуют более сложные методы, которые могут быть эффективными при работе с большими числами или при требовании более точного результата.
Нахождение кубического корня числа часто встречается в задачах программирования и математического моделирования. Правильное выполнение этой операции требует умения использовать соответствующие функции и методы, а также понимания особенностей работы с числами и вычислениями. Имея навыки нахождения кубического корня, программисты на Python могут успешно решать сложные задачи и улучшать функциональность своих программ.
| Преимущества нахождения кубического корня числа в Python: |
|---|
| Расширение возможностей алгоритмов и программ, требующих работы с объемами или размерами |
| Улучшение точности и качества результатов вычислений |
| Снижение сложности и улучшение эффективности вычислений в задачах трехмерного моделирования |
| Оптимизация процесса оценки и изучения изменения величин в пространстве |
Путь к нахождению кубического корня в языке программирования Python

В этом разделе мы рассмотрим шаги, необходимые для нахождения кубического корня из заданного числа в языке программирования Python. Этот процесс позволит нам получить значение, которое при возведении в куб даст исходное число.
Для начала мы будем использовать встроенную функцию pow() языка Python, которая позволяет возвести число в заданную степень. Мы также будем использовать метод sqrt() из модуля math, чтобы найти квадратный корень числа. Затем, опираясь на эти инструменты, мы сможем приступить непосредственно к нахождению кубического корня.
| Шаг | Описание |
|---|---|
| Шаг 1 | Импортируйте модуль math в свою программу. Он предоставит нам доступ к функции sqrt(), необходимой для нахождения квадратного корня числа. |
| Шаг 2 | Задайте исходное число, из которого нужно найти кубический корень. Это может быть либо числовая константа, либо переменная, содержащая числовое значение. |
| Шаг 3 | Примените функцию pow(), чтобы возвести исходное число в степень 1/3 (третью степень). Это даст нам кубическую корень числа. |
| Шаг 4 | Распечатайте результат для получения значения кубического корня. Мы получим числовое значение, которое является корнем третьей степени из исходного числа. |
Следуя этим шагам, вы сможете успешно находить кубический корень из чисел в языке программирования Python. Это может быть полезно при решении задач, связанных с математическими расчетами или обработкой числовых данных.
Шаг 1: Импорт нужных библиотек
Первый шаг в решении данной задачи заключается в импортировании необходимых модулей, которые позволят нам работать с числами и выполнить вычисления. Для этого мы используем инструменты, предоставляемые языком программирования Python.
Шаг 2: Задайте числовое значение для извлечения корня

Раздел "Шаг 2: Задайте числовое значение для извлечения корня" представляет собой этап выбора числа, из которого требуется извлечь корень третьей степени в программе Python. На этом шаге вы устанавливаете основу для последующего вычисления корня третьей степени из данного числа.
Шаг 3: Определение значения третьего квадратного корня
В данном разделе мы рассмотрим методы и алгоритмы для нахождения значения третьего квадратного корня из числа. Мы представим вам несколько способов выполнить данную операцию, которые помогут вам эффективно решать задачи связанные с третьей степенью корней.
Один из эффективных методов для нахождения корня третьей степени - это использование итерационных вычислений. Мы раскроем детали этого подхода и приведем примеры кода на Python, чтобы вы могли легко применять его в своих проектах.
| Метод | Описание |
|---|---|
| Метод Ньютона | Позволяет приближенно находить корень третьей степени. Он основан на итеративных вычислениях, которые приближенно находят значение корня, уточняя его на каждой итерации. |
| Метод Де Кастельо | Представляет собой метод решения третьей степени с использованием формулы, основанной на дробях. Он обеспечивает более точное значение корня третьей степени в сравнении с методом Ньютона. |
Кроме того, мы рассмотрим и другие подходы к нахождению корня третьей степени, такие как использование встроенных функций и математических библиотек Python. Вы узнаете, как использовать эти инструменты для эффективного и точного вычисления третьего квадратного корня.
Примеры получения кубического корня в языке программирования Python

В этом разделе представлены примеры кода на языке Python, которые демонстрируют, как находить кубический корень числа. Результаты вычислений могут быть использованы для решения различных задач: от нахождения объёма геометрических фигур до решения уравнений и алгоритмов.
1. Использование оператора **
Один из способов получить кубический корень числа в Python - использовать оператор ** с величиной, равной 1/3. Например, для нахождения кубического корня из числа 27:
num = 27
cube_root = num ** (1 / 3)
print(f"Кубический корень числа {num} равен {cube_root}")В результате выполнения данного кода будет выведено:
Кубический корень числа 27 равен 3.0
2. Использование функции pow()
Другим способом нахождения кубического корня в Python является использование функции pow(). В качестве первого аргумента передается число, из которого нужно извлечь кубический корень, а вторым аргументом - 1/3. Например:
num = 64
cube_root = pow(num, 1 / 3)
print(f"Кубический корень числа {num} равен {cube_root}")Результат выполнения кода:
Кубический корень числа 64 равен 4.0
3. Использование библиотеки math
В Python существует библиотека math, в которой имеется функция cbrt(), предназначенная для нахождения кубического корня числа. Для ее использования необходимо импортировать модуль math и вызвать функцию cbrt() с аргументом - число, из которого нужно извлечь кубический корень. Например:
import math
num = 125
cube_root = math.cbrt(num)
print(f"Кубический корень числа {num} равен {cube_root}")Результат выполнения:
Кубический корень числа 125 равен 5.0
Таким образом, в Python существуют различные способы нахождения кубического корня числа. Выбор конкретного метода зависит от контекста задачи и предпочтений программиста.
Пример 1: Решение для положительного числа
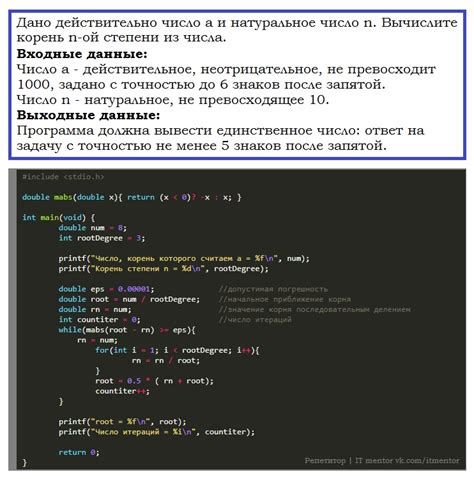
В данном разделе мы рассмотрим исчисление корня третьей степени из положительного числа. Будут представлены шаги решения, которые помогут вам найти значение корня третьей степени.
Для начала, необходимо выбрать положительное число, из которого мы хотим извлечь корень третьей степени. Затем следует использовать соответствующий математический алгоритм и функцию в Python для определения значения корня третьей степени. Обратите внимание, что значение корня третьей степени всегда будет положительным.
Примеры решения для положительных чисел будут приведены ниже, чтобы помочь вам лучше понять процесс нахождения корня третьей степени в Python.
Отрицательные числа и корни третьей степени: пример 2

В данном разделе мы рассмотрим пример нахождения корня третьей степени из отрицательного числа с использованием языка программирования Python.
Если у вас имеется отрицательное число и вам необходимо найти его корень третьей степени, Python предоставляет специальную функцию, позволяющую выполнить это действие. В этом примере мы рассмотрим, как использовать эту функцию для получения корня третьей степени из отрицательного числа.
Для начала, импортируем модуль math в нашу программу:
import mathЗатем, создадим переменную, которой присвоим значение отрицательного числа, из которого мы хотим извлечь корень третьей степени:
number = -27И наконец, используя функцию pow() из модуля math, мы найдем корень третьей степени из данного числа:
result = math.pow(number, 1/3)В результате, значение переменной result будет равно корню третьей степени из отрицательного числа -27.
Таким образом, без использования сложных математических операций и с помощью всего лишь нескольких строк кода на языке Python, мы смогли найти корень третьей степени из отрицательного числа.
Вопрос-ответ

Как найти корень третьей степени из числа в Python?
Для нахождения корня третьей степени из числа в Python можно воспользоваться встроенной функцией **pow()** или оператором **\*\***. Например, если нам нужно найти корень третьей степени из числа 27, мы можем использовать следующий код: **result = pow(27, 1/3)** или **result = 27 ** (1/3)**. В обоих случаях переменная **result** будет содержать корень третьей степени из числа 27, равный 3.



