Когда мы решаем квадратное уравнение, мы используем формулу дискриминанта. Дискриминант позволяет определить, сколько корней у уравнения и каков их характер. Особый случай – когда дискриминант равен нулю. Это означает, что у уравнения есть один корень.
Для нахождения корня уравнения в случае, когда дискриминант равен нулю, нужно воспользоваться формулой. Если уравнение имеет вид ax^2 + bx + c = 0, а дискриминант равен нулю, то корень можно найти по формуле: x = -b / 2a. Этот способ вычисления очень прост и эффективен.
Таким образом, когда дискриминант квадратного уравнения равен нулю, мы знаем, что у уравнения есть один корень, и можем легко найти этот корень, применяя формулу x = -b / 2a. Этот метод поможет вам быстро и точно решить уравнение, не тратя лишнего времени и усилий.
Алгоритм для нахождения корня уравнения
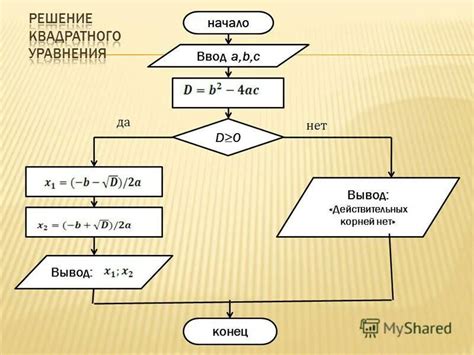
Для нахождения корня уравнения вида ax^2 + bx + c = 0 при равенстве дискриминанта нулю следует выполнить следующие шаги:
1. Вычислить дискриминант по формуле D = b^2 - 4ac.
2. Проверить, если D = 0, то уравнение имеет один корень: x = -b / 2a.
3. Итак, корень уравнения найден.
Использование коэффициентов и дискриминанта

| Коэффициент | Формула |
|---|---|
| Дискриминант D | $D = b^2 - 4ac$ |
| Корни уравнения | Если $D = 0$, то $x_1 = x_2 = \frac{-b}{2a}$ |
При равенстве дискриминанта нулю, у уравнения будет один корень, который можно найти по формуле $x = \frac{-b}{2a}$.
Вопрос-ответ

Как найти корень уравнения, если дискриминант равен нулю?
Для уравнения вида ax^2 + bx + c = 0, если дискриминант равен нулю, то корни будут одинаковыми и равными x = -b/(2a). Это связано с тем, что при дискриминанте равном нулю у уравнения будет один корень.
Почему при равенстве дискриминанта нулю у уравнения один корень?
Когда дискриминант уравнения равен нулю, это означает, что подкоренное выражение в формуле для нахождения корней равно нулю. В таком случае у уравнения будет один корень, так как разность корней равна нулю, следовательно, они равны друг другу.
Каковы формулы для нахождения корней уравнения при равенстве дискриминанта нулю?
При равенстве дискриминанта нулю для уравнения ax^2 + bx + c = 0 можно найти корни по формуле x = -b/(2a). Эта формула позволяет найти корень уравнения, когда дискриминант равен нулю и корни совпадают.
Как вывести формулу для корня уравнения при равенстве дискриминанта нулю?
Для вывода формулы корня уравнения при равенстве дискриминанта нулю можно использовать свойство квадратных уравнений, которое гласит, что если дискриминант равен нулю, то у уравнения будет один корень. Из этого свойства следует формула корня x = -b/(2a) при условии d = b^2 - 4ac = 0, где d - дискриминант.
Как правильно использовать коэффициенты уравнения для нахождения корня при равенстве дискриминанта нулю?
Для нахождения корня уравнения при равенстве дискриминанта нулю можно воспользоваться коэффициентами a, b и c уравнения ax^2 + bx + c = 0. При равенстве дискриминанта нулю формула для нахождения корня будет x = -b/(2a), где коэффициенты a и b идут из исходного уравнения.



