Представьте себе, что вы обладаете способностью считывать загадочные символы на бумажке, по-настоящему поймать каждую дрожь пера и раскроить все глубины геометрических тайн. Этот невероятный дар позволяет вам рассмотреть скрытые стороны окружности, исследовать лабиринты ее углов и найти код кратности в ее сердце. И сегодня мы отправляемся в эту увлекательную экспедицию, чтобы раскрыть одну из самых необычных тайн: как найти часть окружности только по известному углу.
Он заманчиво манит своим загадочным обликом – угол. Геометрический символ, олицетворяющий грани мира и плоскости, угол является важной частью формул и уравнений, куда лишь мудрецы решаются покорить его тайну.
Но не превозноситься лишь тем, что известны лишь некоторые аспекты науки об углах – что ждет нас, если мы решим открыть новую главу в нашем путешествии? Между мифами и реальностью лежит океан неожиданностей и открытий. И сегодня мы окунемся в этот бескрайний мир, чтобы разгадать великую загадку: как найти часть окружности лишь по углу, затаившему свою истинную сущность.
Определение понятия "сегмент круга" и его связь с углом
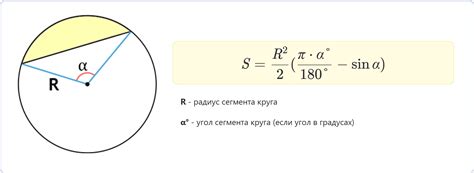
В данном разделе мы рассмотрим понятие сегмента круга и важную связь, которая существует между этим понятием и углом. Говоря простыми словами, сегмент круга представляет собой часть круга, ограниченную дугой и соответствующими ей двумя радиусами.
В геометрии сегмент круга обладает специфическими свойствами и может быть определен разными способами. Одним из ключевых факторов, влияющих на форму сегмента, является угол. Угол, как правило, измеряется в градусах и определяет расстояние между сторонами сегмента и центральным углом круга.
Связь между сегментом круга и углом очень тесная и прямая. Зная значение угла и радиуса круга, мы можем определить площадь и длину дуги, составляющей сегмент. Более того, мы можем вычислить измерения дуги и сегмента, используя соответствующие формулы и выражения. Это позволяет нам более точно анализировать и изучать сегменты окружности в контексте углов и их свойств.
Что такое сегмент окружности? Как он отличается от окружности?

Сегмент окружности – это часть плоскости, ограниченная дугой окружности и двумя радиусами, проведенными к концам дуги. Таким образом, сегмент окружности является частью окружности, ограниченной двумя углами, чей вершиной является центр окружности.
Отличительной особенностью сегмента окружности является наличие двух свободных концов. Дуга окружности, ограниченная сегментом, имеет измеренную длину, задаваемую углом в радианах или градусах. Это позволяет использовать сегменты окружности для вычислений, измерений и построений различных геометрических фигур.
Еще одним важным отличием сегмента окружности от самой окружности является его площадь. Площадь сегмента окружности может быть вычислена с использованием специальных формул. Она зависит от угла, опирающегося на центр окружности, и радиуса окружности.
Важно понимать, что сегмент окружности является лишь частью самой окружности. Знание и понимание различий между этими двумя понятиями может быть полезно для решения геометрических задач и углубленного изучения окружностей и их особенностей.
Таким образом, сегмент окружности является ограниченной дугой фигурой, имеющей свободные концы, измеряемую длину и площадь. Отличие сегмента окружности от окружности состоит в его форме, ограниченных концах и возможности рассчитать его площадь. Это важные понятия в геометрии, используемые для решения различных задач и изучения свойств окружностей.
Взаимосвязь между углом и долей окружности: основные принципы
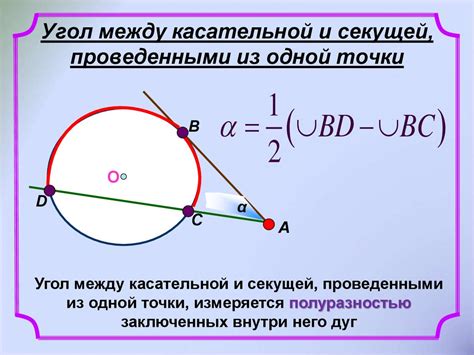
Во-первых, угол в геометрии представляет собой фигуру, образованную двумя лучами, исходящими из одной точки - вершины угла. Угол измеряется в градусах или радианах и может быть острый, прямой, тупой или полный.
С другой стороны, доля окружности представляет собой часть ее длины, которая может быть выражена в процентах или в виде десятичной дроби. Доля окружности и угол между радиусами, соответствующими этой доле, имеют тесную связь.
Если рассматривать полную окружность, то 360 градусов (или 2π радиан) составляют ее полный угол. Таким образом, можно определить соответствие между углом и долей окружности: полный угол соответствует 100% доли окружности.
Определить долю окружности по заданному углу можно, используя пропорциональные соотношения. Если угол меньше полного, тогда доля окружности будет меньше 100%. Если угол больше полного, то доля окружности будет больше 100%. Аналогично, определить угол по заданной доле окружности можно, используя обратные пропорциональные соотношения.
Понимание взаимосвязи между углом и долей окружности позволяет решать различные геометрические задачи и углублять знания о свойствах окружности и ее составляющих элементах.
Соотношение угла и доли окружности: использование для определения
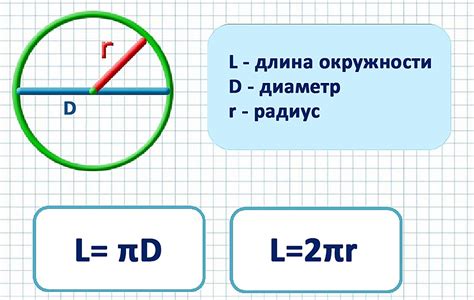
В данном разделе мы рассмотрим, как угол связан с долей окружности и как это соотношение может быть использовано для определения неизвестных значений.
Окружность - это геометрическая фигура, представляющая собой замкнутую кривую, состоящую из всех точек, равноудаленных от ее центра. Угол, с другой стороны, является мерой поворота вокруг определенной точки.
Важно понимать, что угол, измеряемый в градусах или радианах, может быть связан с долей окружности. Доля окружности - это фрагмент окружности, выраженный в процентах или долях от общей длины окружности.
Используя соотношение между углом и долей окружности, мы можем определить неизвестные значения, такие как углы, доли окружности или длины дуги. Зная одно значение, мы можем вывести другие через пропорцию.
Для более точного определения необходимо использовать геометрические формулы и связи между углами и долями окружности. Это позволит нам точно расчитать нужную величину без необходимости производить дополнительные измерения.
Важные формулы и правила для определения доли окружности по заданному углу
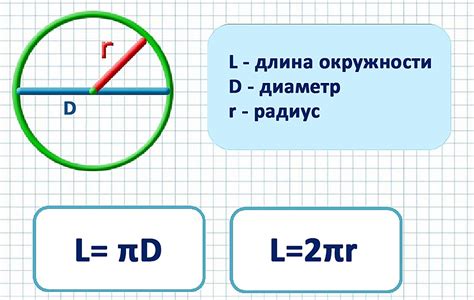
Для эффективного решения задач, связанных с определением доли окружности по заданному углу, необходимо обладать соответствующим набором формул и правил. Эти инструменты позволяют точно и быстро определить требуемую часть окружности, избегая ошибок и неточностей. Давайте рассмотрим некоторые из важных формул и правил, которые помогут вам легко решать подобные задачи.
1. Формула для расчета длины дуги окружности по углу
Одной из ключевых формул, которую необходимо знать, является формула для расчета длины дуги окружности по заданному углу. Эта формула позволяет определить, какую часть от всей окружности составляет заданный угол. Для простоты подсчета используется следующая формула:
длина_дуги = (2πR * α) / 360где длина_дуги - длина дуги окружности, π - математическая константа, R - радиус окружности, α - величина заданного угла в градусах.
2. Формула для определения площади сегмента окружности по углу
Еще одной полезной формулой для нахождения части окружности по углу является формула для расчета площади сегмента окружности. Эта формула позволяет определить, какая площадь окружности приходится на заданный угол. Для вычисления площади сегмента окружности используется следующая формула:
площадь_сегмента = (R² * α) / 2где площадь_сегмента - площадь сегмента окружности, R - радиус окружности, α - величина заданного угла в градусах.
3. Правило трех углов для определения отношения доли окружности к углу
Кроме формул, существуют и важные правила, которые могут помочь в определении отношения доли окружности к заданному углу. Одно из таких правил - правило трех углов, которое гласит: сумма углов дуги окружности и ее противолежащего угла равна 180 градусам. Это правило позволяет определить пропорцию между углом и долей окружности, сделав подсчет более легким и понятным.
Зная формулы и правила, описанные выше, вы сможете эффективно решать задачи, связанные с определением части окружности по заданному углу. Следуя этим инструкциям, вы сможете точно и быстро получить искомый результат, избегая ошибок и неточностей в процессе решения задач.
Формулы и принципы для вычисления доли окружности по заданному углу
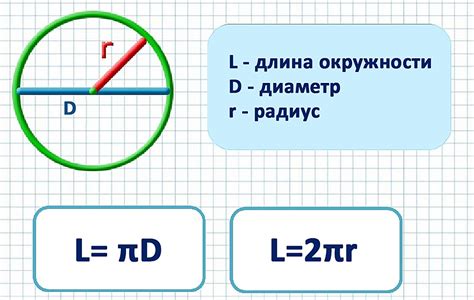
В данном разделе мы рассмотрим некоторые ключевые формулы и правила, позволяющие определить долю окружности, основываясь на заданном угле. Мы изучим способы вычисления этой величины без использования непосредственных понятий, относящихся к нахождению доли окружности.
1. Основные понятия:
Перед тем, как приступить к вычислениям, необходимо понять основные термины и понятия, связанные с окружностью и ее частями. Например, для наших целей необходимо уяснить, что окружность состоит из 360 градусов и что полный оборот равен 2π радианам.
2. Формула пересчета:
Для определения доли окружности по заданному углу используется следующая формула: доля = (угол / 360) * длина окружности. Величина угла указывается в градусах, а длина окружности - в соответствующих единицах (например, метрах или сантиметрах).
3. Связь с радианами:
Конвертирование угла из градусов в радианы может быть полезным при вычислении доли окружности. Для этого можно воспользоваться следующей формулой: угол в радианах = (угол в градусах * π) / 180. После пересчета угла в радианы, можно использовать формулу из предыдущего пункта для определения доли окружности.
4. Примеры использования:
Предлагаем рассмотреть несколько примеров, которые помогут лучше понять основы использования формул и правил для определения доли окружности по заданному углу. При решении этих примеров старайтесь учесть все перечисленные формулы и принципы.
Запомните, что для вычисления доли окружности по заданному углу существует несколько подходов, использующих различные формулы и правила. Определяйте метод в зависимости от конкретной задачи и области применения, и будьте уверены в правильности своих вычислений.
Вопрос-ответ

Как найти длину дуги окружности, если известен центральный угол?
Длина дуги окружности равна произведению длины окружности на соотношение между центральным углом и полным углом. Формула для расчета длины дуги: L = (2πr * α) / 360, где L - длина дуги, r - радиус окружности, α - центральный угол.
Как найти площадь сектора окружности с заданным углом?
Площадь сектора окружности можно найти, используя формулу: S = (πr^2 * α) / 360, где S - площадь сектора, r - радиус окружности, α - центральный угол.
Если известна длина дуги окружности и радиус, как найти меру центрального угла?
Мера центрального угла выражается через длину дуги окружности и радиус по формуле: α = (L * 360) / (2πr), где α - центральный угол, L - длина дуги, r - радиус окружности.
Как найти радиус окружности, если известна длина дуги и центральный угол?
Радиус окружности можно вычислить, зная длину дуги и центральный угол, по формуле: r = (L * 360) / (2πα), где r - радиус окружности, L - длина дуги, α - центральный угол.
Как найти длину окружности, если известен радиус и центральный угол?
Длина окружности можно найти, используя формулу: L = (2πr * α) / 360, где L - длина окружности, r - радиус, α - центральный угол.



