Куда бы нас не занесли увлекательные путешествия в пространстве, мы всегда будем обращать внимание на формы и фигуры, которые нас окружают. Одной из самых впечатляющих и гармоничных среди них является пирамида. Ее стройная конусообразная форма и грандиозность всегда привлекали внимание людей. И сегодня у нас есть возможность заглянуть в саму глубину этой величественной фигуры - узнать ее объем, используя методику, основанную на точках в трехмерном пространстве.
Оказывается, объем пирамиды можно определить по координатам вершин - точек, которые являются углом этой фигуры. Хотите научиться этому искусству и стать настоящим мастером пирамидальной геометрии? Тогда загляните под кат!
Вас ждет увлекательное исследование трехмерных координатных пространств, которое поможет вам погрузиться в мир пирамидальной геометрии. Вы узнаете, как задавать координаты вершин пирамиды, как проводить вычисления объема и как применить эти знания на практике. Вас ожидают увлекательные задания и интересные примеры, которые помогут закрепить полученные знания и развить вашу пирамидальную интуицию.
Разбор основных понятий: координаты углов пирамиды
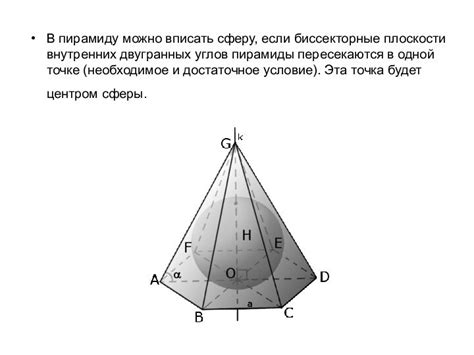
Для работы с пирамидами и расчета их объема по координатам вершин необходимо понимать основные термины и понятия, связанные с координатами углов.
| Термин | Описание |
|---|---|
| Вершина | Точка пирамиды, в которой сходятся ее грани. У каждой вершины есть уникальные координаты, задающие ее положение в пространстве. |
| Координаты | Числовые значения, определяющие положение точек в трехмерном пространстве. Для каждой вершины пирамиды нужно знать ее координаты, чтобы определить ее положение в соответствующей системе координат. |
| Система координат | Упорядоченный набор правил, определяющих способ задания координат. Существуют различные типы систем координат, такие как декартова, цилиндрическая, сферическая и другие. В контексте нахождения объема пирамиды чаще всего используется декартова система координат. |
| Трехмерное пространство | Пространство, состоящее из трех взаимно перпендикулярных осей: оси X, оси Y и оси Z. В трехмерном пространстве определяются положения точек, в том числе вершин пирамиды, с помощью трех чисел - координат по осям X, Y и Z соответственно. |
| Угол | Грань пирамиды, образованная двумя сторонами и вершиной. Углы пирамиды могут быть различной формы и размера, что оказывает влияние на ее объем и форму. |
Понимание этих основных понятий поможет вам правильно работать с координатами вершин пирамиды и последующим расчетом ее объема.
Понятие координат в трехмерном пространстве
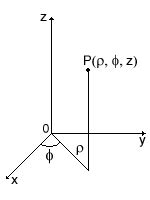
Раздел "Понятие координат в трехмерном пространстве" позволит вам понять основные принципы и концепции работы с координатами в трехмерной системе.
В повседневной жизни мы привыкли ориентироваться в двухмерном пространстве с помощью координатной плоскости, где каждая точка имеет две координаты: абсциссу (x-координату) и ординату (y-координату). Однако, для работы с трехмерными объектами необходимо введение третьей координаты - оси z. При этом каждая точка в трехмерном пространстве определяется тремя координатами: x, y и z.
Трехмерные координаты позволяют точно указать положение объектов в пространстве. Ось x отвечает за горизонтальное перемещение, ось y - за вертикальное перемещение, а ось z - за перемещение вперед или назад. Система трехмерных координат образует прямоугольную декартову систему, в которой каждой точке в пространстве соответствует ее уникальный набор координат.
Знание понятия трехмерных координат является основой для понимания и работы с пирамидами и другими трехмерными фигурами. Зная координаты вершин пирамиды, мы сможем рассчитать её объем и выполнить другие необходимые операции в трехмерном пространстве.
Описание вершины пирамиды и основные параметры, определяющие её форму
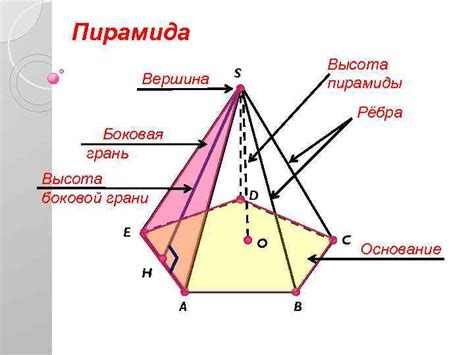
Высота вершины - это расстояние между вершиной пирамиды и её основанием. Она задает разницу в высоте между вершиной и самой нижней точкой этой фигуры. Чем выше находится вершина пирамиды, тем выше объем этого объекта.
Углы наклона рёбер - это углы, образуемые рёбрами пирамиды, возникающие в точках их соединения с вершиной. Они играют важную роль в определении формы пирамиды и служат для построения наглядных представлений данного геометрического объекта.
Радиусы основания - это значения радиусов окружности или сторон треугольной площадки, на которой опирается пирамида. Радиусы основания также влияют на форму и размер объемной фигуры.
Ориентация вершины - это положение точки вершины относительно основания пирамиды. Она может находиться выше, ниже или быть на одном уровне с плоскостью основания. Ориентация вершины дополняет описание формы и структуры пирамиды.
Определение объема пирамиды на основе координат вершин
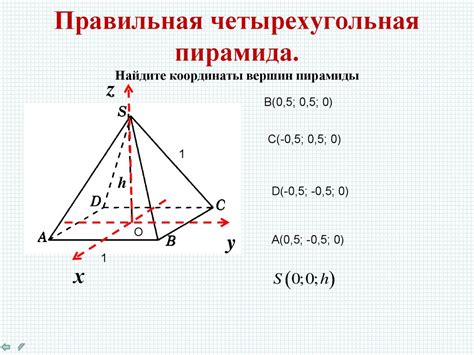
Для расчета объема пирамиды по координатам вершин необходимо применить соответствующую математическую формулу. Вначале необходимо определить основание пирамиды, представляющее собой многоугольник с заданными координатами. Затем нужно найти расстояние от вершины пирамиды до каждой стороны основания. Для этого можно воспользоваться формулой расстояния между двумя точками в трехмерном пространстве. Полученные значения необходимо умножить на площадь основания пирамиды и разделить на 3, чтобы найти объем.
Важно отметить, что для корректного расчета объема пирамиды необходимо, чтобы все вершины основания лежали в одной плоскости, а вершина пирамиды была выше этой плоскости.
Исследование процесса определения объема пирамиды на примере
Раздел, который детально описывает шаги, необходимые для расчета объема пирамиды на основе координат ее вершин. В этом руководстве будут рассмотрены ключевые шаги алгоритма, а также предоставлены примеры, чтобы помочь вам лучше понять процесс.
1. Определение базовой площади и высоты
Первый шаг заключается в определении площади основания пирамиды и высоты. Базовая площадь является основанием пирамиды, а высота - расстоянием от базы до вершины. Для определения площади основания можно использовать формулы геометрических фигур, таких как прямоугольник или треугольник.
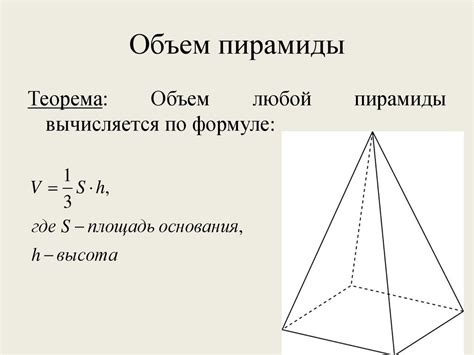
2. Нахождение объема по формуле
После определения базовой площади и высоты пирамиды можно приступить к рассчету объема. Формула для расчета объема пирамиды зависит от ее формы. Для простого случая, когда пирамида имеет треугольное основание, формула будет выглядеть следующим образом: V = (1/3) * S * h, где V - объем пирамиды, S - площадь основания, h - высота.
3. Пример расчета
Чтобы лучше понять процесс расчета объема, рассмотрим пример. Допустим, у нас есть пирамида с треугольным основанием и следующими координатами вершин: A(0, 0), B(4, 0), C(2, 3) и вершиной D(2, 5). Сначала определим площадь треугольника ABC с помощью геометрической формулы. Затем найдем высоту пирамиды, которая будет равна расстоянию от вершины D до плоскости ABC. Подставив все найденные значения в формулу, мы сможем найти объем пирамиды.
Вопрос-ответ

Как найти объем пирамиды по координатам вершин?
Для того чтобы найти объем пирамиды по координатам вершин, можно воспользоваться формулой Герона. Сначала необходимо найти площадь основания пирамиды, используя формулу площади треугольника. Затем вычислить высоту пирамиды, которая является расстоянием от вершины пирамиды до плоскости основания. После нахождения площади основания и высоты, можно применить формулу для расчета объема пирамиды: V = (S * h) / 3, где V - объем пирамиды, S - площадь основания, h - высота пирамиды.
Как найти площадь основания пирамиды по координатам вершин?
Для нахождения площади основания пирамиды по координатам вершин необходимо воспользоваться формулой площади треугольника. Сначала нужно выбрать любые три точки из координат вершин пирамиды, чтобы образовать треугольник. Затем применить формулу Герона для нахождения площади треугольника. Повторить этот процесс для каждой тройки точек и сложить площади всех треугольников, чтобы получить площадь основания пирамиды.
Как найти высоту пирамиды по координатам вершин?
Для нахождения высоты пирамиды по координатам вершин нужно найти расстояние от вершины пирамиды до плоскости основания. Для этого можно воспользоваться формулой площади треугольника и формулой плоскости. Сначала выберите три точки из координат вершин, чтобы образовать треугольник основания. Затем найдите площадь этого треугольника. После этого используйте формулу плоскости, чтобы найти уравнение плоскости основания. Затем найдите расстояние от вершины пирамиды до плоскости основания, применив формулу расстояния от точки до плоскости. Таким образом, вы найдете высоту пирамиды.



