Всегда ли вы чувствовали уверенность в том, что знаете, как определить характеристики разнообразных фигур? Наверняка, каждому из нас приходилось сталкиваться с задачами, связанными с определением площади и периметра: возможно, при занятиях математикой в школе или при решении повседневных проблем. В любом случае, четкое понимание этих понятий и навык их вычисления являются неотъемлемыми компонентами нашей жизни.
Как же найти нужные значения, не превращаясь в настоящего «зомби-математика»? Важно искать методы, которые позволяют с точностью и легкостью решить поставленную задачу вне зависимости от ее сложности и формы фигуры. Этим методам нет равных в своей эффективности и практичности.
В данной статье мы предлагаем вам погрузиться в мир поиска площадей и периметров с помощью пошаговых алгоритмов и универсальных приемов. Мы расскажем о способах, которые помогут вам разобраться в тонкостях измерения фигур, не углубляясь в сложные математические теории и определения. Ведь понимая базовые принципы, вы сможете справиться с любыми проблемами, которые захочет поставить перед вами безжалостное реальное мир.
Основные принципы и формулы для вычисления периметра и площади геометрических фигур
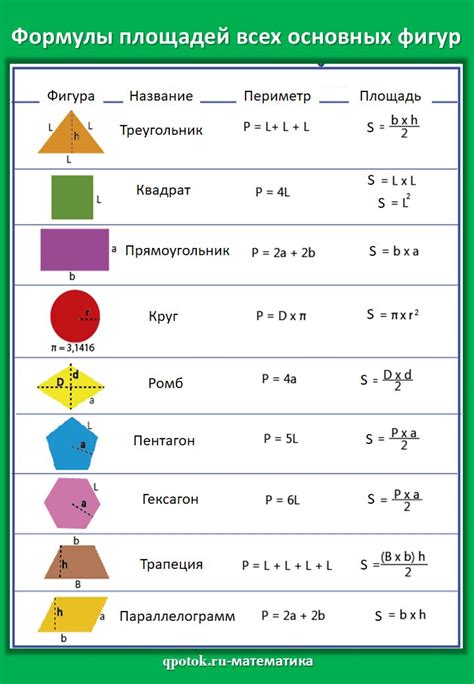
В данном разделе мы рассмотрим общие принципы и формулы, которые помогут вам находить периметр и площадь различных геометрических фигур. Знание этих основных принципов позволит вам расчитывать периметр и площадь самостоятельно и с легкостью.
Периметр фигуры представляет собой сумму длин всех ее сторон и является мерой длины самой границы фигуры. Найдя периметр фигуры, мы узнаем, сколько длины нужно, чтобы обойти ее по контуру.
Некоторые примеры популярных геометрических фигур, для которых можно посчитать периметр, включают треугольник, квадрат, прямоугольник, круг и шестиугольник.
Площадь фигуры выражает понятие площади плоской фигуры и представляет собой меру площади ограничиваемой ею поверхности. Зная площадь фигуры, мы можем определить, сколько площади она занимает на плоскости.
Для вычисления площади различных геометрических фигур используются соответствующие формулы, такие как формула для площади треугольника, формула для площади прямоугольника, формула для площади круга и т. д.
Знание принципов и формул для вычисления периметра и площади позволит вам решать разнообразные задачи, связанные с геометрией и конструированием. Начните с освоения базовых принципов и формул, а затем применяйте их на практике для решения более сложных задач.
Зачем нужны периметр и площадь и почему они имеют важное значение
Понимание периметра и площади помогает нам решать множество задач, связанных с определением длины контура фигуры и площади ее поверхности. Например, периметр используется при расчете необходимого количества материала для обводки или ограждения фигуры, а площадь позволяет нам узнать, сколько площади занимает та или иная поверхность, что может быть полезно при планировании размещения объектов или решении задач из области географии.
Понимание и умение работать с периметром и площадью являются важными навыками, не только для профессионалов в различных сферах, но и для каждого человека в повседневной жизни. Знание этих концепций позволяет нам более точно измерять, анализировать и планировать, способствуя более эффективному использованию ресурсов и принятию осознанных решений.
Раздел 1. Методы и принципы вычисления периметра фигуры

В этом разделе мы рассмотрим различные способы определения периметра для разных геометрических фигур. Вы узнаете, какие шаги необходимо выполнить и как использовать различные формулы, чтобы точно определить периметр фигуры.
1. Расчет периметра треугольника
Для вычисления периметра треугольника нужно просуммировать длины всех его сторон. В зависимости от известных данных, можно использовать различные методы, такие как применение сторон треугольника или использование координат точек треугольника для расчета расстояний между ними.
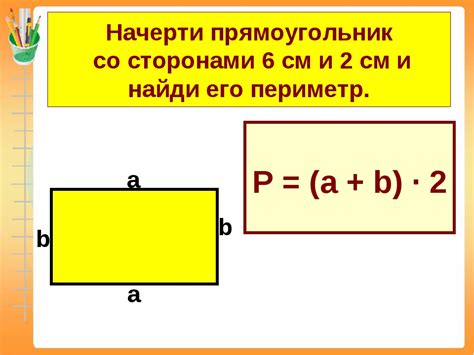
2. Расчет периметра прямоугольника
Периметр прямоугольника можно вычислить, зная длину его сторон. Чтобы определить периметр, нужно просуммировать длины всех сторон прямоугольника. Если длина и ширина прямоугольника известны, можно использовать следующую формулу: периметр = 2 * (длина + ширина).
3. Расчет периметра окружности
Для вычисления периметра окружности нужно знать ее радиус либо диаметр. Если известен радиус, то формула для расчета периметра будет следующей: периметр = 2 * π * радиус, где π (пи) – это математическая константа, примерно равная 3,1415. Если известен диаметр, периметр можно найти с помощью формулы: периметр = π * диаметр.
4. Расчет периметра других фигур
Для некоторых фигур с более сложной геометрией есть специальные формулы и методы для определения периметра. Например, для вычисления периметра ромба нужно знать длины его сторон, а для расчета периметра эллипса – его полуоси. В этом разделе вы также узнаете о методах вычисления периметра этих и других фигур.
Таблица 1: Примеры формул для вычисления периметра
| Фигура | Формула для вычисления периметра |
|---|---|
| Треугольник | Сумма длин всех сторон |
| Прямоугольник | 2 * (длина + ширина) |
| Окружность | 2 * π * радиус (или π * диаметр) |
| Ромб | 4 * длина стороны ромба |
Разнообразные методы вычисления площадей различных фигур

У вычисления площади фигур существует множество подходов, позволяющих определить площадь с помощью различных формул и методов. В данном разделе мы рассмотрим несколько из них, которые позволят найти площадь фигур с определенной точностью и эффективностью.
Рассмотрим вычисление общей длины и площади треугольника
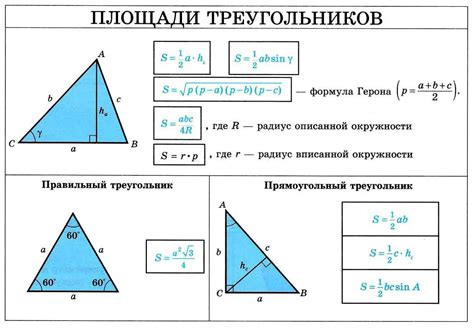
В данном разделе мы рассмотрим конкретные способы расчета границ треугольника, включая общую длину его сторон и его площадь. Мы представим несколько примеров, чтобы показать, как проводятся эти расчеты, избегая использования основных терминов.
Одним из способов определить длину треугольника является измерение каждой его стороны и сложение полученных значений. Другой метод включает использование известного угла, отклоняясь от которого, и определение длины боковой стороны с использованием теоремы косинусов. Также можно применить синусы и косинусы для определения длин боковых сторон и углов треугольника в соответствии со сторонами.
Рассчитывая площадь треугольника, можно использовать различные методы. Одним из наиболее простых способов является использование формулы "половина основания умножить на высоту". Другим вариантом является использование теоремы Пифагора для определения длины основания и высоты, а затем умножение полученных значений. Использование формулы Герона для расчета площади с помощью длин всех сторон треугольника также будет рассмотрено в данном разделе.
| Пример треугольника | Метод расчета периметра | Метод расчета площади |
|---|---|---|
| Прямоугольный треугольник | Измерение сторон и их сложение | Половина основания, умноженная на высоту |
| Равносторонний треугольник | Умножение длины стороны на 3 | Основание, умноженное на высоту, разделенное на 2 |
| Разносторонний треугольник | Измерение сторон и их сложение | Формула Герона: S = sqrt(p * (p - a) * (p - b) * (p - c)), где a,b,c - стороны треугольника и p - полупериметр |
Примеры вычисления периметра и площади прямоугольника
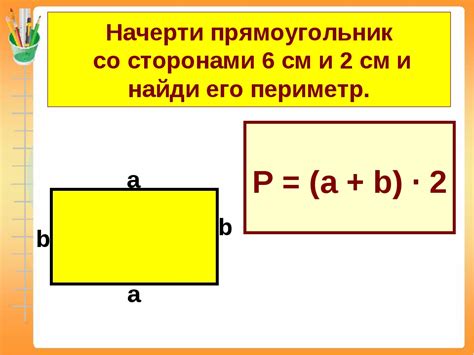
В данном разделе представлены интересные и практические примеры, где можно узнать, как посчитать периметр и площадь прямоугольника. Мы рассмотрим различные сценарии, которые помогут вам разобраться в этом важном математическом процессе.
Прямоугольник - это геометрическая фигура, которая имеет две параллельные стороны, противоположные углы равны между собой. Он широко используется в повседневной жизни и в различных областях, таких как строительство, дизайн и математика.
Для расчета периметра прямоугольника, нужно сложить все его стороны. Мы покажем вам, как найти периметр, используя значения сторон прямоугольника и применяя формулу, которая поможет вычислить эту величину с точностью и безошибочно.
В том же разделе вы узнаете, как вычислить площадь прямоугольника, которая представляет собой произведение длины и ширины этой фигуры. Мы покажем простой способ применения этой формулы и предоставим вам примеры для лучшего понимания процесса.
Необходимость знать, как вычислить периметр и площадь прямоугольника может быть полезной во многих ситуациях, например, при ремонте помещения или научных расчетах. Приобретение таких навыков поможет вам стать более компетентным и уверенным в различных математических задачах, связанных с прямоугольниками.
Изучение методов вычисления площади и периметра круга
В данном разделе мы рассмотрим примеры расчета площади и периметра круга, используя различные методы и формулы. Будут приведены практические примеры, которые помогут уяснить основные концепции и подходы к вычислению данных характеристик для данной геометрической фигуры.
Для начала, рассмотрим метод вычисления площади круга. Одним из способов расчета является использование формулы, основанной на радиусе круга. Мы подробно рассмотрим этот метод и приведем примеры его применения на практике.
Далее, обратим внимание на метод вычисления периметра круга. В данном случае, мы будем использовать формулу, которая также основывается на радиусе круга. Показав примеры расчета периметра, мы поможем вам лучше понять эту характеристику круга.
И наконец, мы сравним различные подходы к вычислению площади и периметра круга, чтобы понять, какой метод более предпочтителен в определенных ситуациях. В конце раздела вы сможете легче определить наиболее эффективный способ расчета этих характеристик для ваших задач.
Образцы вычисления периметра и площади многоугольника
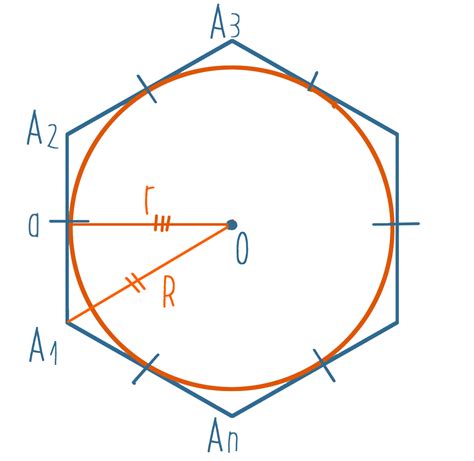
В этом разделе представлены конкретные примеры расчета общей длины границы и площади многоугольников. Вы узнаете, как применить различные методы для определения периметра и площади фигуры, а также научитесь применять их в практических случаях.
Мы рассмотрим примеры с различными типами многоугольников: треугольниками, четырехугольниками и многоугольниками с более чем четырьмя сторонами. Каждый пример будет иметь подробное объяснение того, как получить необходимые значения.
Вам будут предложены шаги, которые необходимо выполнить для нахождения периметра и площади каждого многоугольника. Вы сможете использовать эти методы для самостоятельного расчета периметра и площади любой фигуры, представленной вам.
Начнем с простых примеров и постепенно перейдем к более сложным многоугольникам. В конце вы будете готовы вычислять периметр и площадь любого многоугольника, используя различные методы и формулы.
Секреты ускорения вычислений площади и периметра: безошибочные алгоритмы и эффективные подходы
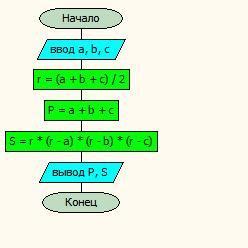
В этом разделе мы погрузимся в увлекательный мир вычислений площади и периметра, и я расскажу вам о некоторых секретах, которые помогут значительно ускорить процесс.
Перед тем как приступить к расчетам, важно понять основные принципы каждой фигуры и определить, какие из них применимы к конкретной задаче. Перед вами открывается бесконечное множество возможностей для нахождения площади и периметра, и грамотный выбор подхода может значительно сократить время и усилия, затрачиваемые на вычисления.
Один из самых эффективных способов ускорить расчеты - использование формул и алгоритмов, разработанных специально для каждой фигуры. При этом необходимо помнить, что некоторые фигуры имеют разные возможности для вычисления их площади и периметра с использованием разных формул. Так что стоит экспериментировать и выбирать наиболее удобные и эффективные методы для своих конкретных задач.
Кроме использования формул, стоит обратить внимание на различные геометрические свойства, которые могут значительно ускорить расчеты. Например, для многоугольника можно воспользоваться методом разбиения на треугольники и вычисления площадей каждого из них отдельно. Это позволит избежать сложных вычислений и значительно сократить время, затрачиваемое на определение площади.
Кроме того, стоит обратить внимание на возможность использования автоматизированных инструментов и программ для расчета площади и периметра. Существуют специальные программы и онлайн-ресурсы, которые позволяют быстро и точно считать площадь и периметр различных фигур. Отличительной особенностью таких инструментов является их точность и удобство использования.
Вопрос-ответ

Как найти периметр треугольника?
Для нахождения периметра треугольника нужно сложить длины всех его сторон. Например, если у вас есть треугольник со сторонами длиной 5, 7 и 9 единиц, то периметр будет равен 5 + 7 + 9 = 21 единица.
Как найти площадь квадрата?
Площадь квадрата можно вычислить, умножив длину одной его стороны на себя. Например, если сторона квадрата равна 6 единицам, то площадь будет равна 6 * 6 = 36 квадратных единиц.
Как найти периметр и площадь прямоугольника?
Периметр прямоугольника можно найти, сложив длины всех его сторон. Например, если длины сторон прямоугольника равны 4 и 6 единиц, то периметр будет равен 2 * (4 + 6) = 20 единиц. Чтобы найти площадь прямоугольника, нужно умножить длину одной стороны на длину другой стороны. В данном примере, площадь будет равна 4 * 6 = 24 квадратных единиц.



