Арифметика в начальной школе – это первое знакомство учеников с миром чисел, форм и пространства. На этом этапе обучения дети получают основные навыки и знания, которые в дальнейшем помогут им легко ориентироваться в математических задачах и реальной жизни. Один из важных разделов арифметики в 3 классе – изучение площадей и периметров фигур.
Площадь и периметр – два основных понятия, которые помогают определить размеры и формы различных объектов, будь то здания, садовые участки или картинки на бумаге. При изучении этих характеристик учащиеся узнают, каким образом можно установить количество занимаемого пространства и длину окружности или сторону фигуры. Важно отметить, что площадь и периметр являются важными компонентами не только в математике, но и в других науках и областях знания, таких как архитектура, строительство и география.
В рамках изучения площадей и периметров в 3 классе, методика Моро предлагает интуитивный подход к пониманию этих понятий. С помощью игровых и практических заданий, ученики могут в интерактивной форме исследовать различные фигуры и определить их площадь и периметр. Этот метод позволяет ученикам понять основные принципы расчета характеристик фигур и развить навыки критического мышления и пространственного воображения.
Как определить площадь треугольника с помощью формулы Моро?

Формула Моро - это математическое выражение, которое позволяет нам вычислить площадь треугольника по длинам его сторон и двум углам (или одному углу и длине противолежащей стороны). При помощи этой формулы мы можем точно определить площадь треугольника без необходимости измерять его высоту или использовать другие сложные методы.
Давайте рассмотрим основные шаги для применения формулы Моро:
- Измерьте длины всех трех сторон треугольника. Обозначим их как a, b и c.
- Найдите значение полупериметра треугольника (p), сложив длины всех сторон и разделив полученную сумму на 2.
- Используя формулу Моро, вычислите площадь треугольника по следующей формуле: S = √(p * (p - a) * (p - b) * (p - c)). Здесь S - площадь треугольника.
Теперь мы знаем, как использовать формулу Моро для определения площади треугольника. Используя данную формулу, мы можем решать задачи на определение площади треугольника различной формы и размера. Упражняйтесь в применении этой формулы, и вы сможете легко решать задачи по геометрии!
Основные понятия и измерение площади в математике
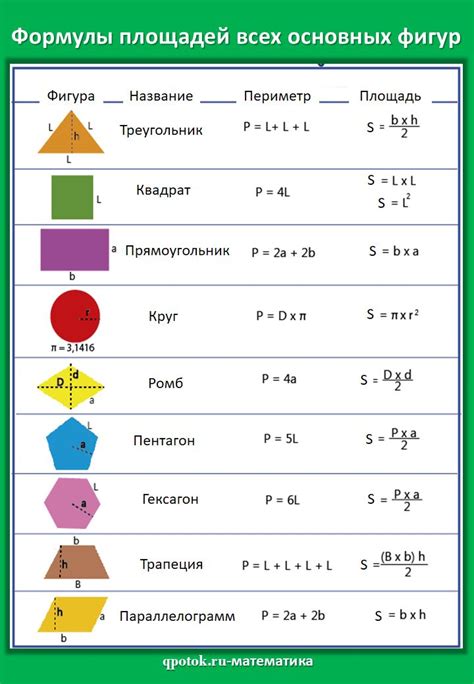
Для измерения площади используются различные методы, которые зависят от формы фигуры. Например, для прямоугольника площадь можно найти, умножив длину на ширину. Для треугольника можно использовать формулу, включающую основание и высоту. Другие фигуры, такие как круг или эллипс, имеют свои специальные формулы для расчета площади.
Измерение площади является важным навыком, который помогает нам анализировать и сравнивать разные геометрические фигуры. Площадь может быть выражена в разных единицах измерения, таких как квадратные метры, квадратные сантиметры или квадратные дюймы, в зависимости от конкретной задачи.
Понимание и измерение площади позволяют нам анализировать различные объекты и их отношения, а также решать разнообразные задачи связанные с пространством и поверхностью. Навыки работы с площадью часто используются в строительстве, архитектуре, геометрии, и других областях, где необходимо анализировать и управлять пространственными объектами.
Описание и характеристики треугольника в геометрии
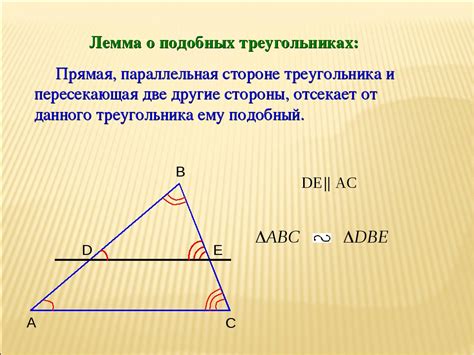
В треугольнике можно выделить такие характеристики, как длины сторон, углы, периметр и площадь. Длины сторон определяются измерением расстояния между вершинами, углы - это меры поворота сторон, периметр - сумма всех сторон, а площадь - показатель покрывающей треугольник площади.
Треугольники могут быть разных типов в зависимости от величин углов и длин сторон. Например, равносторонний треугольник имеет все стороны равными, прямоугольный треугольник имеет один прямой угол, а разносторонний треугольник имеет все стороны и углы различными.
Изучение треугольников в геометрии помогает понять и применять их свойства в различных задачах, включая вычисление площади и периметра. Знание особенностей и характеристик треугольника позволяет более глубоко понять и анализировать геометрические объекты. Треугольники являются основой для понимания и построения других более сложных фигур и объектов в геометрии.
| Понятие | Описание |
| Треугольник | Геометрическая фигура, состоящая из трех сторон и трех вершин. |
| Длины сторон | Расстояния между вершинами треугольника. |
| Углы треугольника | Меры поворота сторон треугольника. |
| Периметр | Сумма всех сторон треугольника. |
| Площадь | Показатель покрывающей треугольник площади. |
| Типы треугольников | Равносторонний, прямоугольный, разносторонний. |
Формула Моро и вычисление площади треугольника
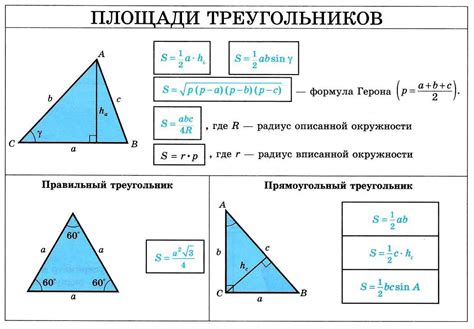
В обучении математике для третьего класса хорошо известна формула Моро, которая позволяет вычислить площадь треугольника без необходимости использования его высоты. Это простой и удобный способ определить, сколько единиц площади принадлежит данной фигуре.
Итак, каким образом работает формула Моро?
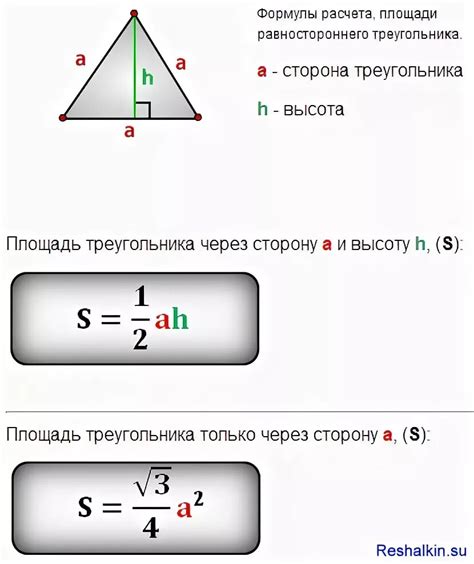
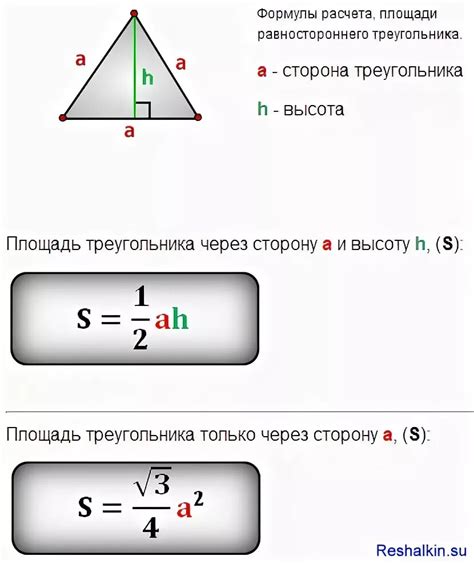
В основе этой формулы лежит произведение длины основания треугольника и длины прямоугольника, построенного на данном основании.
Пусть О - основание треугольника, а H - длина прямоугольника, построенного на данном основании. Тогда площадь треугольника вычисляется, как половина произведения О и H.
Таким образом, для любого треугольника можно использовать формулу Моро для определения его площади, учитывая только основание и длину прямоугольника, построенного на данном основании. Это простой и эффективный метод, который позволяет избежать сложных вычислений и использования высоты треугольника.
Идеи для решения задач по нахождению площади треугольника
В этом разделе представлены примеры решения задач, связанных с нахождением площади треугольника. Мы рассмотрим различные методы и подходы, чтобы помочь вам легко и точно решать такие задачи. Вы узнаете о различных формулах и правилах, которые позволяют вычислить площадь треугольника. Эти примеры помогут вам развить навыки и уверенность в решении подобных задач.
1. Метод основания и высоты: Этот метод использует длину основания (стороны треугольника) и перпендикулярную высоту, опущенную на эту основу. Мы рассмотрим примеры, где будем находить значения этих параметров и применять соответствующую формулу для расчета площади треугольника.
2. Метод полупериметра и радиуса вписанной окружности: Этот метод применяется, когда известны длины всех сторон треугольника. Мы научимся находить полупериметр, радиус вписанной окружности и по этим значениям вычислять площадь треугольника.
3. Метод Герона: Этот метод используется для нахождения площади треугольника, если известны длины всех трех сторон. Мы рассмотрим примеры, где будем применять формулу Герона для вычисления площади треугольника и шаг за шагом разберем процесс решения.
- Пример 1: Нахождение площади треугольника по длинам основания и высоты.
- Пример 2: Вычисление площади треугольника по значениям всех сторон.
- Пример 3: Использование формулы Герона для нахождения площади треугольника.
Формула Моро для вычисления периметра треугольника
Что такое периметр и как он определяется в геометрии?

Периметр можно представить как путь, который нужно пройти по всем сторонам фигуры. Он измеряется в линейных единицах, таких как сантиметры или метры. Периметр фигуры позволяет нам понять, насколько длинной будет нить, если ее провести вдоль границы этой фигуры.
Определение периметра различается в зависимости от вида геометрической фигуры. Например, для прямоугольника или квадрата, периметр равен сумме длин всех его сторон. В то же время, для круга, периметр называется окружностью и определяется как произведение числа Пи (π) на двойной радиус окружности.
Понимание периметра помогает нам измерять и сравнивать размеры различных фигур. Он также находит свое применение в решении задач, связанных с площадью и другими параметрами фигур.
Итак, периметр - это важное понятие в геометрии, которое помогает измерять длину границы фигуры и понимать ее размеры. Знание определения периметра различных фигур позволяет нам решать задачи и углублять наши знания в геометрии.
Особенности вычисления периметра треугольника по формуле Моро
- Определение длины сторон треугольника
- Суммирование длин сторон
- Расчет периметра треугольника
Первым шагом при вычислении периметра треугольника по формуле Моро является определение длин его сторон. Для этого необходимо использовать известные значения и синтаксические упражнения, чтобы найти длину каждой стороны треугольника.
После определения длин сторон треугольника необходимо сложить значения вместе для получения суммы длин сторон. Эта сумма будет использоваться для расчета периметра треугольника по формуле Моро.
Используя формулу Моро, периметр треугольника может быть вычислен путем умножения суммы длин сторон на половину этой суммы. Результатом будет периметр треугольника, выраженный в соответствующих единицах измерения.
Вычисление периметра треугольника по формуле Моро позволяет быстро и точно определить общую длину всех его сторон, что является важным элементом при изучении геометрии и решении различных задач, связанных с треугольниками.
Примеры решения задач по определению общей длины сторон треугольника
В данном разделе мы рассмотрим примеры решения задач, связанных с определением периметра треугольника. Периметр - это сумма длин всех сторон треугольника.
Пример 1:
Пусть треугольник ABC имеет стороны со следующими длинами: AB = 5 см, BC = 4 см и AC = 3 см. Найдем его периметр.
Для этого сложим длины всех сторон: 5 см + 4 см + 3 см = 12 см.
Ответ: Периметр треугольника ABC равен 12 см.
Пример 2:
Пусть треугольник XYZ имеет периметр равный 15 см, а сторона XZ равна 6 см. Найдем длины оставшихся сторон треугольника.
Для этого вычтем из общего периметра длину стороны XZ: 15 см - 6 см = 9 см.
Разделим полученную сумму на 2, так как остались две стороны YZ и YX, которые равны между собой: 9 см / 2 = 4,5 см.
Ответ: Стороны YZ и YX треугольника XYZ равны 4,5 см каждая.
Следуя данным примерам, вы сможете успешно решать задачи на нахождение периметра треугольников. Запомните основные правила вычислений и не забывайте проверять ваш результат!
Вопрос-ответ

Как найти площадь прямоугольника?
Чтобы найти площадь прямоугольника, нужно умножить длину одной стороны на длину другой стороны. Например, если длина прямоугольника равна 5 см, а ширина равна 3 см, то площадь будет равна 5 см * 3 см = 15 квадратных сантиметров.
Как найти периметр квадрата?
Периметр квадрата вычисляется путем сложения длин всех его сторон. Если сторона квадрата равна 8 см, то периметр будет равен 8 см + 8 см + 8 см + 8 см = 32 см.
Как найти площадь треугольника?
Для вычисления площади треугольника нужно умножить длину его основания на высоту и разделить полученное значение пополам. Например, если основание треугольника равно 6 см, а высота равна 4 см, то площадь будет равна (6 см * 4 см) / 2 = 12 квадратных сантиметров.
Как найти периметр окружности?
Периметр окружности вычисляется умножением диаметра окружности на число Пи (приближенное значение равно 3,14) или умножением радиуса окружности на число Пи и затем на 2. Например, если диаметр окружности равен 10 см, то периметр будет равен 10 см * 3,14 = 31,4 см.



