Море комплексных чисел. Древнейшие наставления мудрых говорят, что круг является великим символом бесконечности и гармонии. Как же не устремить взор к таинственным свойствам окружности, которые привлекали в себе веками. Крылатая фраза "приближенно равно" помогает в понимании ее мистического характера.
Откроем врата знания. В каждой математической ветви прячется свой фрагмент пазла, формирующий общую картину мира. В рамках нашего погружения в мир тригонометрии, познакомимся с одним из наиболее загадочных символов – комплексными числами. Потрясающая их способность утвердиться в различных областях знания – главное, что их однозначно привлекает общественность. А это уже веский аргумент, помимо сегодняшней научно-технической значимости.
Сводим все к общему. В группе математических дисциплин, делятся функции, очень сильно связанные. Важно, чтобы они поддерживали взаимоотношения друг с другом и явно демонстрировали это. Этот блок наглядно показывает, какие непреходящие константы помогают справиться с самыми различными задачами, где одно допускает употребление другого. Они столь схожи, что дозволительно назвать их близнецами в сложных применениях.
Основные понятия и определения

В данном разделе мы рассмотрим основные ключевые понятия, которые связаны с изучением свойств и характеристик системы, где приводятся синонимы для представления идей и понятий.
Аргументом функции называется независимая переменная, или величина, которая влияет на значение определенной функции. В контексте нашей темы, аргументом может быть угол, относительно которого мы определяем синус и косинус.
Значение функции от аргумента - это результат применения функции к данному аргументу, который может представлять как числовое, так и геометрическое значение. Например, при рассмотрении угла на окружности, значение функции может быть синусом или косинусом этого угла.
Циклическая функция - это функция, значения которой повторяются через определенный интервал или период. В данном контексте, функции синус и косинус являются циклическими, поскольку их значения повторяются при изменении угла на окружности.
Период функции - это наименьшая положительная длина угла, при которой значения функции повторяются. В случае с синусом и косинусом, периодом является 360 градусов или 2π радианы, так как значения этих функций повторяются после полного оборота по окружности.
Амплитуда - это максимальное абсолютное значение функции в течение периода. В случае с синусом и косинусом, амплитуда равна 1, так как значения этих функций изменяются от -1 до 1 при любом угле на окружности.
Фаза функции - это точка на периоде, от которой начинается изменение значения функции. В контексте углов на окружности, фазу можно определить как начальный угол, от которого отсчитываются значения синуса и косинуса.
Геометрическое значение тригонометрических функций на окружности
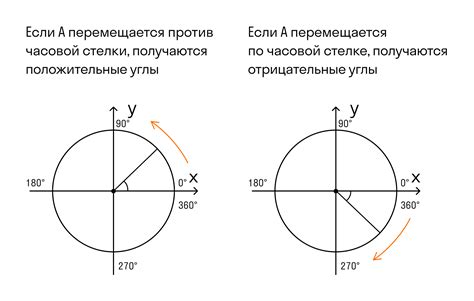
В данном разделе рассмотрим геометрическую интерпретацию функций, которые описывают зависимость между углом и отношением сторон прямоугольного треугольника на окружности.
Функция, которая описывает отношение стороны, примыкающей к углу, к длине гипотенузы прямоугольного треугольника на окружности, называется именно синусом. Эта функция позволяет нам определить, насколько удалена точка на окружности от начальной точки, пройдя угол, измеряемый против часовой стрелки от оси OX.
В свою очередь, функция, которая описывает отношение стороны, примыкающей к углу, к длине гипотенузы прямоугольного треугольника на окружности, называется косинусом. Косинус позволяет нам определить, насколько удалена точка на окружности от начальной точки, пройдя угол, измеряемый против часовой стрелки от оси OY.
Таким образом, геометрическая интерпретация синуса и косинуса на окружности помогает нам определить положение точки на окружности после прохождения определенного угла. Эти функции являются основными тригонометрическими функциями, которые находят широкое применение в различных областях науки и техники.
Геометрический метод определения значения тригонометрических функций на периметре круга
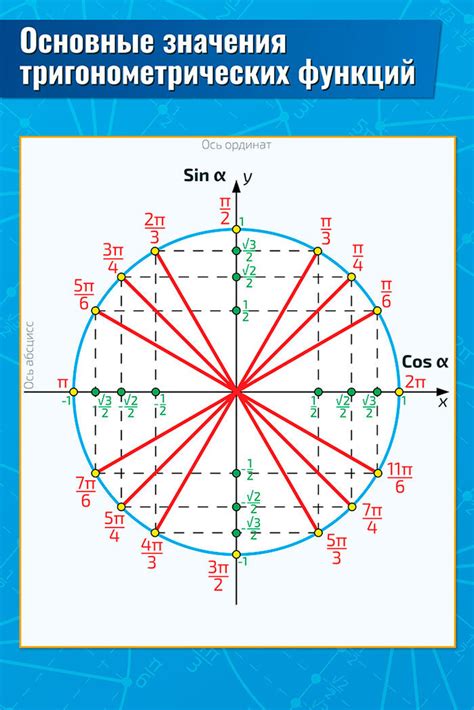
Древними математиками был разработан инновационный метод для определения значений синуса и косинуса на окружности с использованием геометрических принципов. Этот подход позволяет вычислить значения тригонометрических функций, не полагаясь на алгебраические формулы или таблицы. Вместо этого, эти функции могут быть выразительно изучены и обобщены в терминах геометрических свойств плоских фигур, таких как прямоугольные треугольники и единичная окружность.
Главная идея геометрического метода заключается в использовании единичной окружности – окружности радиусом 1 единица – как основы для определения значений синуса и косинуса. Одна из наиболее важных особенностей единичной окружности состоит в том, что длина дуги между любыми двумя точками на окружности пропорциональна углу, образованному этими точками.
Применяя геометрические принципы, значения синуса и косинуса могут быть представлены в виде отношений длин сторон прямоугольного треугольника, образованного радиусом единичной окружности и линией, проходящей через точку на окружности и ось координат. Это позволяет определить синус и косинус любого угла, образованного такой линией и положительной полуосью абсцисс, без использования специальных таблиц или математических формул.
Тригонометрическая окружность и связь с синусом и косинусом
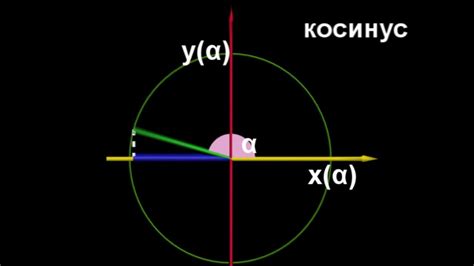
Тригонометрическая окружность является основой для понимания синуса и косинуса, двух основных тригонометрических функций. Синус и косинус могут быть определены как значения координат точек на окружности в зависимости от угла, проведенного от начальной точки. Используя эту связь, мы можем выразить синус и косинус через углы и отношения сторон треугольника, что позволяет нам решать разнообразные задачи и применять тригонометрию на практике.
Таблица значений тригонометрических функций при различных углах
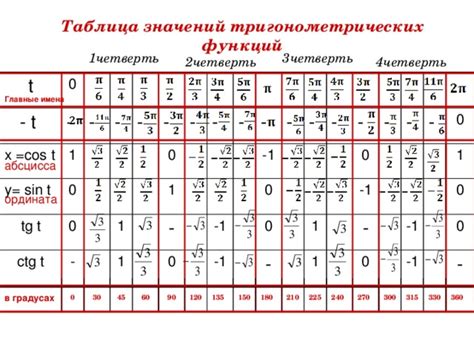
| Угол (градусы) | Синус | Косинус |
|---|---|---|
| 0° | 0 | 1 |
| 30° | 0.5 | 0.866 |
| 45° | 0.707 | 0.707 |
| 60° | 0.866 | 0.5 |
| 90° | 1 | 0 |
Это лишь небольшой фрагмент таблицы, которую можно использовать для нахождения значений синуса и косинуса при других углах. Зная значения синуса и косинуса для различных углов, вы можете легко решать тригонометрические задачи, а также использовать эти функции для нахождения расстояний, высот, времени и многих других параметров.
Операции с тригонометрическими функциями в геометрическом контексте

В данном разделе мы рассмотрим основные операции с тригонометрическими функциями в контексте геометрии, где нам необходимо работать с окружностями. Используя понятия отношения сторон в прямоугольном треугольнике и его соответствующее представление на координатной плоскости, мы сможем выполнять вычисления тригонометрических функций без использования стандартных формул и таблиц.
Главными объектами в данной геометрической интерпретации тригонометрических функций являются точки на единичной окружности и соответствующие им углы. Рассмотрим каждую операцию более подробно.
Получение синуса угла
Чтобы получить значение синуса угла, мы ищем ординату (y-координату) точки на окружности, которая соответствует данному углу. Таким образом, можно сказать, что синус угла – это проекция радиуса на ось ординат.
Получение косинуса угла
Для получения значения косинуса угла, мы ищем абсциссу (x-координату) точки на окружности, соответствующей данному углу. То есть, можно сказать, что косинус угла – это проекция радиуса на ось абсцисс.
Используя данные операции с синусом и косинусом на окружности, мы можем определить значение этих функций для любого угла, имея только его меру. Это позволяет нам упростить вычисления и использовать тригонометрию в различных сферах, таких как физика, инженерия и естественные науки.
Применение тригонометрических функций в решении задач

Одно из главных применений синуса и косинуса заключается в определении отношений сторон треугольника. Используя различные соотношения между углами и сторонами треугольника, мы можем определить значения этих функций и использовать их для решения широкого спектра задач.
Тригонометрические функции также широко используются в физике. Они позволяют определить законы движения тела, траектории движения, а также предсказывать и анализировать различные физические явления. Например, с помощью синуса и косинуса можно вычислить максимальную высоту броска тела, его скорость, ускорение и т.д.
Еще одним важным применением синуса и косинуса является решение задач, связанных с колебаниями и волной. Такие задачи встречаются в акустике, оптике, электронике и других областях науки и техники. При анализе колебаний и волн мы используем синусоидальные функции для описания их характеристик и поведения.
| Примеры задач | Применение тригонометрических функций |
|---|---|
| Определение высоты здания по углу наклона его тени | Использование тангенса угла |
| Расчет длины дуги окружности | Применение связи длины дуги с радиусом и углом |
| Нахождение суммы векторов | Использование скалярного произведения векторов и косинуса угла между ними |
Тригонометрические функции синуса и косинуса являются неотъемлемой частью математического аппарата и находят широкое применение в решении различных задач. Понимание и умение использовать эти функции помогает анализировать и предсказывать поведение объектов и явлений в различных областях науки и техники.
Вопрос-ответ

Как найти синус и косинус на окружности?
Синус и косинус на окружности можно найти с помощью геометрических свойств треугольника, образованного радиусом окружности, проведенным до точки на окружности, и осью абсцисс. Синусом угла называется отношение длины противолежащего катета треугольника к длине гипотенузы, а косинусом — отношение длины прилежащего катета к длине гипотенузы.
Насколько точными будут полученные значения синуса и косинуса, найденные на окружности?
Значения синуса и косинуса, найденные на окружности, будут абсолютно точными. Это связано с тем, что радиус окружности является постоянной величиной, а геометрические свойства треугольника, образованного радиусом, позволяют безошибочно определить значения синуса и косинуса.
Какой угол необходимо измерять, чтобы найти синус и косинус на окружности?
Чтобы найти синус и косинус на окружности, необходимо измерять угол между радиусом окружности и осью абсцисс. Данный угол обозначается символом "θ" (тета) и измеряется в радианах.
Какие значения могут принимать синус и косинус на окружности?
Значение синуса и косинуса на окружности может изменяться в диапазоне от -1 до 1. Это связано с геометрическими свойствами треугольника, образованного радиусом и строящимся на окружности.
Могу ли я использовать найденные значения синуса и косинуса на окружности в математических вычислениях?
Да, найденные значения синуса и косинуса на окружности широко используются в математических вычислениях. С их помощью можно решать различные задачи, связанные с геометрией, физикой, инженерией и другими областями науки.
Зачем нужно находить синус и косинус на окружности?
Нахождение синуса и косинуса на окружности является важной задачей в математике и физике. Эти тригонометрические функции позволяют определить соотношения между углами и сторонами прямоугольных треугольников, что является основой для решения множества геометрических и физических задач.



