График функции является важным инструментом для анализа её свойств. Определить, является ли функция отрицательной по графику можно, анализируя поведение кривой на промежутке интереса. Отрицательная функция принимает отрицательные значения на определённом промежутке независимой переменной.
Если график функции на определённом интервале лежит ниже оси X (ось абсцисс), то функция является отрицательной в этом интервале. Следует учитывать, что функция может быть отрицательной только на части своей области значений. Положительный наклон графика относительно оси X может свидетельствовать о том, что функция положительна, а отрицательный наклон может указывать на отрицательную функцию.
Определение отрицательной функции по графику
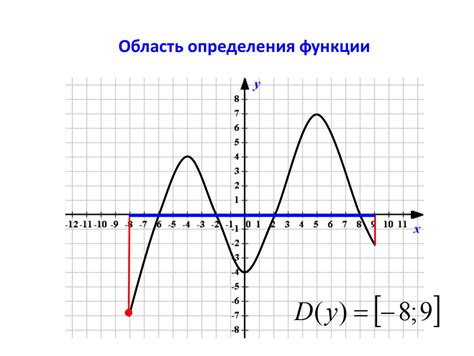
Пример:
Предположим, у нас есть график функции y = -2x. Если график этой функции находится ниже оси Х и не пересекает ее, то это означает, что функция отрицательна на всем промежутке.
Начальные понятия

Для определения знака функции по графику необходимо знать основные понятия:
1. График функции: представляет собой множество точек, координаты которых связаны уравнением функции.
2. Ось абсцисс: горизонтальная ось на графике, отображающая значения аргумента функции.
3. Ось ординат: вертикальная ось на графике, отображающая значения функции.
4. Положительная область: часть графика, находящаяся выше оси абсцисс, где значения функции положительны.
5. Отрицательная область: часть графика, находящаяся ниже оси абсцисс, где значения функции отрицательны.
Исходя из этих понятий можно определить знак функции по графику: если график функции находится выше оси абсцисс, функция положительна; если ниже – функция отрицательна.
Расположение графика функции
Чтобы определить, что функция отрицательна по графику, нужно провести следующие действия:
- Изучить кривизну графика. Функция с отрицательными значениями обычно располагается ниже оси абсцисс.
- Проанализировать угол наклона к оси абсцисс. Если график функции убывает слева направо, значит функция отрицательна.
- Проверить точки пересечения с координатными осями. Если у графика есть точки пересечения с осью ординат в отрицательной области, то функция отрицательна.
Интервалы возрастания и убывания
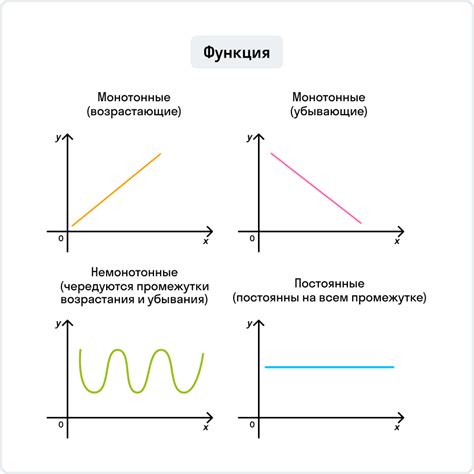
Для определения интервалов возрастания и убывания функции по графику необходимо анализировать наклон касательной к кривой графика в данной точке.
Если наклон касательной в точке x больше нуля, то функция возрастает в этой точке и на интервале вокруг нее. Если наклон отрицателен, то функция убывает.
| Наклон касательной | Функция |
|---|---|
| Положительный | Функция возрастает |
| Отрицательный | Функция убывает |
Точки перегиба и экстремумы
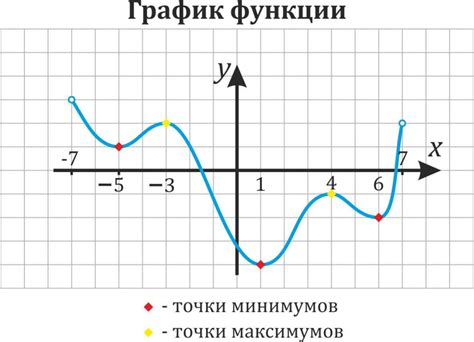
Определение отрицательности на интервалах

Для того чтобы определить, что функция отрицательна на определенном интервале по графику, необходимо анализировать поведение функции на этом интервале. Изучая график функции, следует обращать внимание на то, что значения функции на интервале меньше нуля означают отрицательность функции на данном интервале. Важно учитывать, что функция может менять свое поведение и знак на различных участках графика, поэтому необходимо более детальное изучение графика на каждом интервале.
Анализ температурного графика
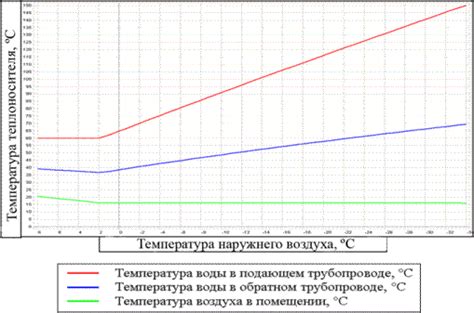
Для определения, что функция отрицательна по графику, необходимо провести анализ температурного графика. Для этого можно использовать следующий алгоритм:
- Оценить изменение температуры во времени
- Выделить участки графика со снижением температуры
- Исследовать процентное соотношение отрицательных значений температуры к положительным
После проведения анализа температурного графика можно сделать заключение о том, что функция демонстрирует отрицательные значения в определенных интервалах времени.
Проверка на точке построения графика
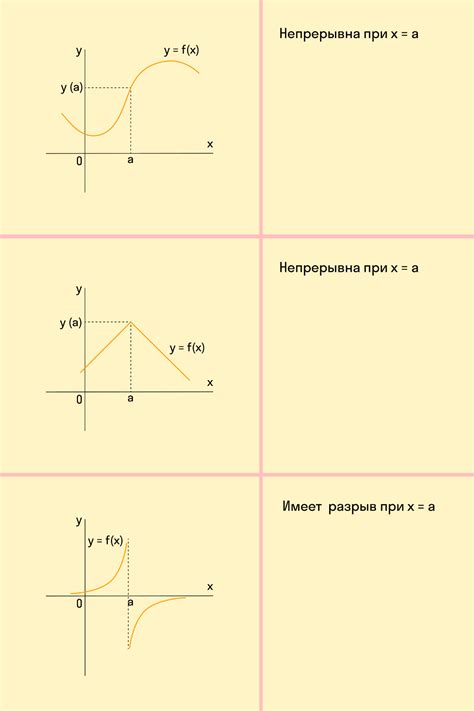
Для определения знака функции от графика можно провести проверку на любой произвольной точке, лежащей на построенном графике функции. Для этого необходимо определить значение функции в данной точке. Если значение функции отрицательно, то функция будет считаться отрицательной в данной точке графика. Если значение функции положительно, то функция будет считаться положительной в данной точке графика.
Вопрос-ответ

Как определить, что функция отрицательна по графику?
Чтобы определить, что функция отрицательна по графику, нужно анализировать положение графика функции относительно оси X. Если график находится ниже оси X на всем промежутке, то функция является отрицательной. Например, если все точки графика находятся под осью X и не пересекают ее, то функция отрицательна.
Как распознать, что график функции принимает отрицательные значения?
Для определения того, что график функции принимает отрицательные значения, достаточно посмотреть на его положение относительно осей координат. Если график функции расположен ниже оси X на участке отображения, то значения функции на этом участке будут отрицательными.
Какие признаки говорят о том, что функция отрицательна по графику?
Основные признаки, что функция отрицательна по графику, это то, что график функции находится ниже оси X на всем интервале определения и не пересекает ее. Также можно отметить, что точки графика функции лежат в отрицательной области координатной плоскости.



