Во время изучения геометрии, одним из наиболее интересных и важных понятий является гипотенуза - наибольший из отрезков в прямоугольном треугольнике. Понимание ее длины и способы ее определения становятся ключевыми задачами для решения многих геометрических проблем.
Существует несколько методов, позволяющих вычислить длину части гипотенузы, используя только информацию о высоте треугольника. Это предоставляет альтернативные способы для определения этой величины и расширяет наш математический инструментарий.
В данной статье мы рассмотрим несколько различных подходов к определению длины отрезка гипотенузы через измерение его высоты. Мы также предоставим наглядные примеры, которые помогут нам лучше понять и визуализировать эти методы. Глубже погрузившись в тему, мы сможем увидеть, как эти альтернативные подходы отличаются друг от друга и как они могут быть полезными в различных геометрических задачах.
Часть гипотенузы и высота треугольника: понятия и связь

Часть гипотенузы - это отрезок, который соединяет вершину треугольника с точкой, в которой он пересекает высоту. Таким образом, часть гипотенузы является сегментом гипотенузы, ограниченным самой гипотенузой и высотой треугольника.
Понимание связи между частью гипотенузы и высотой треугольника помогает нам определить длину этой части. Существуют различные методы для вычисления длины части гипотенузы, одним из которых является использование подобия треугольников. Этот метод основан на том, что подобные треугольники имеют соответствующие стороны, пропорциональные друг другу.
Рассмотрим пример для наглядности. Предположим, у нас есть прямоугольный треугольник с гипотенузой длиной 10 см и высотой равной 6 см. Чтобы найти длину части гипотенузы, мы можем использовать следующую пропорцию: длина части гипотенузы / гипотенуза = высота / длина гипотенузы. Подставляя известные значения, мы можем вычислить длину части гипотенузы: длина части гипотенузы = (6 * 10) / 10 = 6 см.
Таким образом, понимание понятия части гипотенузы и его связи с высотой треугольника помогает нам определить длину этой части с помощью подобия треугольников. Этот метод может быть полезен при решении задач геометрии и обеспечивает более глубокое понимание структуры треугольника.
Что такое отрезок гипотенузы и высота треугольника?

Этот раздел посвящен понятию отрезка гипотенузы и высоты треугольника. Здесь мы рассмотрим основные аспекты данных понятий и их взаимосвязь с треугольником.
Отрезок гипотенузы - это одна из сторон прямоугольного треугольника, которая является наиболее длинной и располагается напротив прямого угла. Он играет важную роль в расчетах и измерениях, связанных с треугольниками. Высота треугольника - это отрезок, проведенный из вершины треугольника к основанию, перпендикулярно к основанию. Она определяет расстояние от основания до вершины и влияет на свойства и характеристики треугольника.
- Отрезок гипотенузы является главной диагональю прямоугольного треугольника.
- Высота треугольника делит его на два прямоугольных треугольника и служит для нахождения площади треугольника.
- Отрезок гипотенузы и высота треугольника взаимосвязаны посредством теоремы Пифагора.
- Высота треугольника влияет на его устойчивость и угловые свойства.
Понимание этих понятий и их связи позволяет лучше понять треугольники, а также использовать их в различных математических и строительных расчетах.
Связь между отрезком гипотенузы и высотой треугольника: понимание взаимосвязи
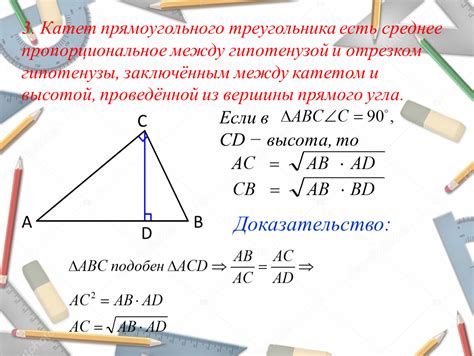
Этот раздел посвящен исследованию связи между определенным отрезком гипотенузы и высотой треугольника. Мы рассмотрим вопрос о том, как величина этого отрезка связана с высотой треугольника и как эта связь может быть полезной при решении задач геометрии.
При изучении геометрических фигур, особенно треугольников, важно понимать, как различные их элементы взаимосвязаны. При работе с треугольниками имеется несколько способов применения высоты, например, для нахождения площади, углов или других длин сторон.
В данном разделе мы сосредоточимся на отрезке, который является частью гипотенузы треугольника. Мы исследуем, как этот отрезок связан с высотой треугольника. Важно отметить, что понимание этой связи может быть полезным для решения различных задач геометрии.
- Мы рассмотрим несколько примеров, иллюстрирующих использование отрезка гипотенузы и высоты треугольника в задачах.
- Будут представлены способы вычисления величины отрезка на основе известных данных, таких как длина других сторон треугольника или размеры углов.
- Также будет рассмотрена взаимосвязь между отрезком гипотенузы и высотой треугольника в разных типах треугольников, включая прямоугольные и непрямоугольные.
Понимание связи между отрезком гипотенузы и высотой треугольника является важным аспектом в изучении геометрии. Это позволяет нам использовать эти соотношения для решения задач и применения их в практических ситуациях.
Различные приемы для расчета отрезка гипотенузы при известной высоте
Рассмотрим разнообразные подходы, которые позволяют определить длину отрезка гипотенузы, используя информацию о высоте треугольника. Вместо четкого определения, мы предлагаем представить общую идею, которая будет полезна для дальнейшего изучения данной темы.
| Метод | Описание |
|---|---|
| Метод подобия треугольников | В данном методе используется свойство подобия треугольников с помощью соответствующих сторон и высоты. Путем использования пропорций можно определить отрезок гипотенузы. |
| Теорема Пифагора | Теорема Пифагора позволяет найти отношение между сторонами прямоугольного треугольника и применить его для определения длины отрезка гипотенузы. |
| Формула Герона | Формула Герона используется для вычисления площади треугольника, а затем можно определить отрезок гипотенузы при известной высоте. |
Это лишь несколько примеров методов, которые можно применить для определения длины отрезка гипотенузы через известную высоту. При изучении данной темы важно учитывать особенности каждого треугольника и выбрать наиболее подходящий метод для конкретной ситуации.
Метод, основанный на применении подобия треугольников
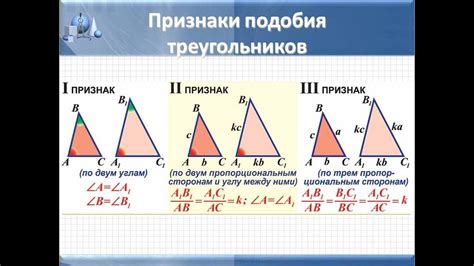
Принцип подобия треугольников - это свойство треугольников, которое гласит, что при совпадении соответственных углов они подобны. Используя этот принцип, мы можем построить пропорции между отрезками треугольников и определить длину искомого отрезка.
Для применения метода с использованием подобия треугольников необходимо иметь информацию о длине одного из отрезков треугольника, высоте и других известных величинах. После вычисления пропорции мы можем определить длину искомого отрезка с высокой степенью точности.
Применение подобия треугольников является эффективным и широко используется в геометрии. Этот метод позволяет решать разнообразные задачи, связанные с определением длины отрезков в треугольниках, в том числе и определение длины части гипотенузы через высоту.
Метод, основанный на теореме Пифагора

Один из способов определения длины части гипотенузы с использованием высоты основан на применении теоремы Пифагора. Этот метод позволяет вычислить длину гипотенузы треугольника, зная длины катета и высоты, опущенной на этот катет.
Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Используя эту теорему, мы можем выразить длину гипотенузы через известные значения других сторон треугольника.
| Дано | Формула | |
|---|---|---|
| Длина катета | a | Известно |
| Длина высоты, опущенной на катет | h | Известно |
| Длина гипотенузы | c | Неизвестно |
Применяя теорему Пифагора, мы можем выразить неизвестную длину гипотенузы следующей формулой:
c = √(a2 + h2)
Где символ √ обозначает операцию извлечения квадратного корня. Используя эту формулу, мы можем вычислить длину части гипотенузы с помощью известных значений длины катета и высоты.
Примеры расчета отрезка гипотенузы с использованием вертикальной линии
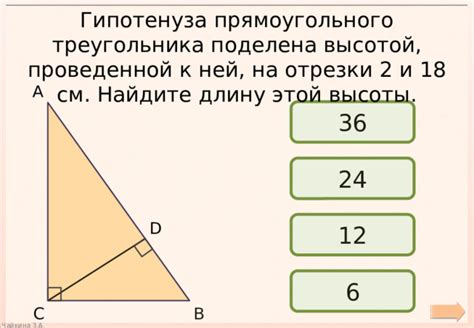
В данном разделе представлены практические примеры, демонстрирующие способы определения длины отрезка гипотенузы с помощью перпендикулярной вертикальной линии. Рассмотрим примеры, чтобы наглядно представить, как работает данный метод и для каких задач он может быть применен.
Пример 1:
Представим, что у нас имеется прямоугольный треугольник, одна сторона которого является гипотенузой. Мы знаем длину гипотенузы и хотим найти длину отрезка, который является частью гипотенузы и перпендикулярен катету. Для этого мы проводим вертикальную линию из точки пересечения гипотенузы с катетом, образуя таким образом два подобных треугольника. Зная исходные данные и используя подобие треугольников, мы можем определить длину отрезка гипотенузы, который нам требуется найти.
Пример 2:
Если мы имеем прямоугольную призму и хотим определить длину отрезка гипотенузы, который проходит через одну из вершин основания и перпендикулярен ему, то также можно воспользоваться этим методом. С помощью конструкции перпендикулярной вертикальной линии, мы создаем подобные треугольники, используя свойства подобия и известные значения, получаем длину искомого отрезка гипотенузы.
Таким образом, представленные примеры помогают наглядно показать, каким образом можно определить длину части гипотенузы с использованием вертикальной линии. Этот метод может быть полезен в различных задачах, связанных с геометрией, строительством и другими областями, где требуется нахождение длин отрезков гипотенузы.
Пример 1: Расчет отрезка гипотенузы в треугольнике ABC
В данном примере мы рассмотрим способ определения длины части гипотенузы треугольника ABC с использованием высоты. Результаты данного расчета позволят нам получить конкретное значение отрезка гипотенузы соответствующего треугольника.
Для начала мы определяем высоту треугольника ABC, а затем, используя полученные значения, приступаем к расчету длины части гипотенузы. Расчеты проводятся по формулам, которые основаны на известных свойствах треугольников.
- Найдем высоту треугольника ABC, обозначим ее как h.
- Подставим значение высоты в соответствующую формулу и рассчитаем длину отрезка гипотенузы.
- Полученный результат представляет собой длину искомого отрезка гипотенузы треугольника ABC.
Таким образом, с использованием данного метода исследования мы можем точно определить длину части гипотенузы треугольника ABC, используя высоту как вспомогательную величину. Этот пример демонстрирует практическое применение математических методов для определения геометрических параметров треугольников.
Пример 2: Вычисление отрезка гипотенузы треугольника XYZ с помощью высоты
- Шаг 1: Найдите длину высоты треугольника XYZ, которая является перпендикуляром, опущенным из вершины треугольника к основанию.
- Шаг 2: Определите длину основания треугольника, которое является отрезком, соединяющим две вершины, не включая вершину, из которой опущена высота.
- Шаг 3: С использованием теоремы Пифагора вычислите длину отрезка гипотенузы треугольника XYZ, используя найденные значения длины высоты и основания.
Теперь рассмотрим пример: Предположим, вы измерили длину высоты треугольника XYZ и нашли, что она равна 8 единицам. Далее, вы определили длину основания, которая составляет 6 единиц. Для вычисления длины гипотенузы треугольника XYZ, применим теорему Пифагора: сумма квадратов длины высоты и длины основания будет равна квадрату длины гипотенузы. Вставляя найденные значения, получим: 8^2 + 6^2 = гипотенуза^2. Дальше, выполняя простые вычисления, найдем длину отрезка гипотенузы треугольника XYZ.
Вопрос-ответ

Что такое гипотенуза и высота треугольника?
Гипотенуза - это сторона треугольника, противолежащая прямому углу. Высота треугольника - это отрезок, проведенный из вершины треугольника к основанию, перпендикулярно основанию.
Как можно определить длину части гипотенузы через высоту треугольника?
Длину части гипотенузы через высоту треугольника можно определить с помощью теоремы Пифагора. Для этого нужно знать длину высоты и длину части гипотенузы от вершины треугольника до основания. Сумма квадратов этих длин будет равна квадрату полной длины гипотенузы.
Какие методы можно использовать для определения длины части гипотенузы через высоту?
Для определения длины части гипотенузы через высоту треугольника можно использовать теорему Пифагора, а также применять подобные треугольники и свойства прямоугольных треугольников.
Можете привести примеры расчета длины части гипотенузы через высоту треугольника?
Конечно! Предположим, у нас есть прямоугольный треугольник с высотой 6 и частью гипотенузы 8. Используя теорему Пифагора, мы можем рассчитать полную длину гипотенузы следующим образом: 8^2 = гипотенуза^2 - 6^2. Подставляя значения, получим 64 = гипотенуза^2 - 36. Далее, проводим несложные вычисления и получаем, что гипотенуза = 10.
Можно ли определить длину части гипотенузы через высоту без использования теоремы Пифагора?
Да, можно. Если у нас есть треугольник со знакомыми углами и высотой, то можно применять свойства подобных треугольников для определения длин. Это может потребовать больше шагов и вычислений, но и без теоремы Пифагора можно определить длину желаемой части гипотенузы через высоту.



