Определение множества значений функции является важным аспектом математики и анализа функций. График функции может дать нам информацию о том, какие значения функции может принимать в определенных интервалах или точках.
Важно помнить, что график функции является лишь визуальным инструментом и не всегда дает точное математическое представление о множестве значений. Для более точного анализа и определения множества значений функции рекомендуется использовать математические методы, такие как дифференцирование, интегрирование или анализ поведения функции в различных точках.
Определение функции по графику
Для определения функции по графику необходимо анализировать поведение кривой на координатной плоскости. Важно учитывать следующие аспекты:
| 1. | Определить, является ли график функцией. Для этого нужно проверить, что каждому значению x соответствует только одно значение y. |
| 2. | Изучить форму графика, чтобы понять его характеристики: возрастание, убывание, экстремумы, асимптоты. |
| 3. | Найти интервалы, где функция определена, и область значений функции. |
| 4. | Определить монотонность функции, используя наклон графика в разных областях. |
Интервалы возрастания и убывания
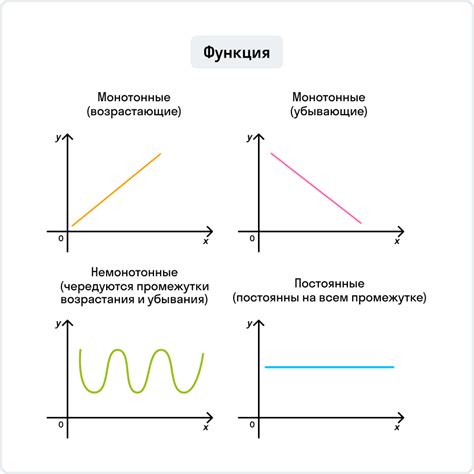
Для определения интервалов возрастания и убывания функции по графику следует обратить внимание на наклон графика. Если график функции идёт "вверх", то это интервал возрастания, а если "вниз" - интервал убывания.
Для более точного определения интервалов возрастания и убывания следует проверять значение производной функции на соответствующих участках графика.
| Интервал возрастания | Интервал убывания |
|---|---|
| График функции идет "вверх" | График функции идет "вниз" |
Точки экстремума функции
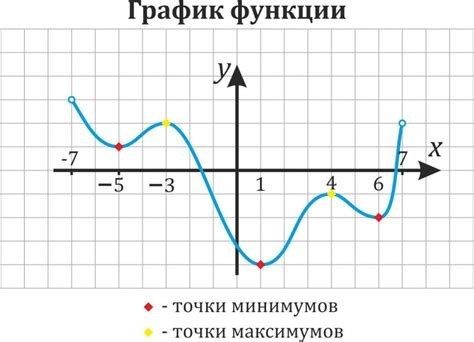
Для определения точек экстремума необходимо найти точки, в которых производная функции равна нулю или не существует. Это могут быть точки локального максимума, минимума или точки перегиба функции.
Определение значений функции
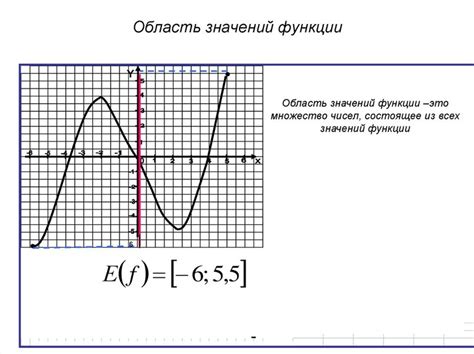
Существование горизонтальных асимптот
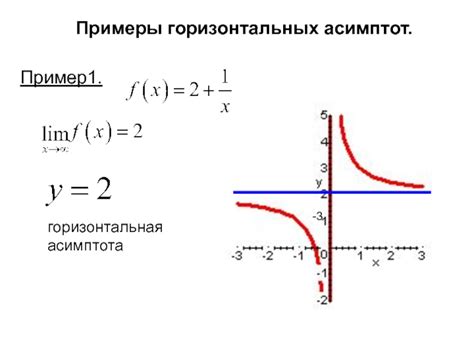
Горизонтальная асимптота функции на графике представляет собой горизонтальную прямую, к которой график стремится при стремлении значения аргумента к бесконечности (или к плюс или минус бесконечности). Горизонтальная асимптота может существовать, если предел функции существует при стремлении аргумента к бесконечности и функция не стремится к бесконечности. Для определения существования горизонтальной асимптоты необходимо анализировать предел функции при стремлении аргумента к бесконечности.
График функции и ее множество значений
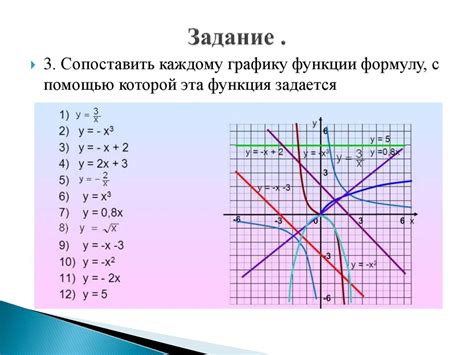
Множество значений функции определяется как набор всех возможных значений, которые функция может принимать при изменении своего аргумента. График функции визуализирует это множество значений на координатной плоскости.
Для того чтобы определить множество значений функции по ее графику, необходимо проследить, какие значения функция принимает по оси Y при различных значениях аргумента по оси X. То есть, нужно исследовать, какие точки на графике соответствуют значениям функции.
Множество значений функции может быть дискретным или непрерывным. Для уточнения этого можно анализировать график функции более подробно, следя за ее изменениями и колебаниями.
Вопрос-ответ

Как определить множество значений функции по графику?
Для определения множества значений функции по графику необходимо просмотреть все уникальные значения, которые принимает функция на своем графике. Это можно сделать, проанализировав вертикальные линии, которые пересекают график функции. Каждая точка пересечения указывает на значение функции в этой точке. Если график функции не пересекает какое-либо значение на оси y, то это значение не входит в множество значений функции. В итоге множество значений функции будет представлять собой все возможные значения, которые принимает функция на своем графике.
Какие методы можно использовать для определения множества значений функции?
Для определения множества значений функции можно использовать различные методы, включая анализ графика функции, решение уравнений, эмпирический анализ и другие. Один из популярных методов - это анализ графика функции, при котором можно определить множество значений функции, рассматривая все возможные значения на оси y, которые пересекаются с графиком функции. Кроме того, можно использовать математическую теорию, чтобы определить область значений функции.
Можно ли определить множество значений функции без графика?
Да, можно определить множество значений функции без графика, используя математические методы. Для этого можно решать уравнения, проводить анализ функции, вычислять пределы и т.д. Например, если функция задана аналитически, то можно проанализировать ее выражение и определить возможные значения переменных, которые могут принимать функция. Это позволит определить множество значений функции даже без графика.



