Если вам когда-либо приходилось определять положение точки в заштрихованной области, то вы знаете, насколько это может быть сложным заданием. Часто, при решении таких задач, требуется обратиться к синтаксическим средствам языка программирования или использовать специальные математические алгоритмы. Однако, даже без глубоких знаний в программировании, вы можете научиться определять, находится ли точка в заштрихованном районе, используя простые методы и интуитивно понятный подход.
Для начала, давайте разберемся с понятием "заштрихованная область". Мы будем использовать этот термин для обозначения конкретной части плоскости, которая имеет определенные границы и отмечена специальным маркером - штриховкой. Можно сказать, что эта область выделяется на фоне всего остального и привлекает внимание к себе.
В нашем случае, мы хотим узнать, находится ли заданная точка внутри или снаружи заштрихованной области. Для этого нам понадобятся некоторые сведения о ее границах и характеризующих ее параметрах. Важно отметить, что в данной статье мы не будем рассматривать сложные математические модели или алгоритмы. Вместо этого, мы сосредоточимся на простых и доступных способах, которые помогут нам быстро определить положение точки внутри или вне штрихованной области.
Защищенные участки и точки внутри них
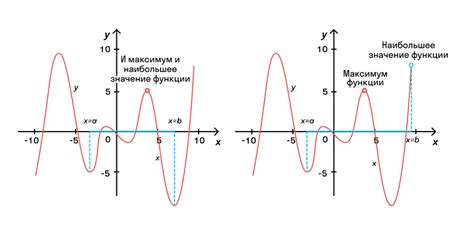
В данном разделе рассматривается проблема определения принадлежности точки к определенной области, которая ограничена исключительными границами. Эти области представляют собой защищенные участки, где точка может находиться внутри границ или за пределами них.
В процессе анализа таких областей, необходимо разработать математическую модель, которая позволит определить географическое положение точки относительно заштрихованной области. Для этого используются различные методы, включая геометрические и алгоритмические подходы.
Одним из самых распространенных методов является разбиение заштрихованной области на более простые геометрические фигуры, такие как полигоны или многоугольники. Затем, с использованием геометрических алгоритмов, проводится проверка принадлежности точки к каждой из этих фигур. Это позволяет определить, находится ли точка внутри или снаружи каждой фигуры.
Другим подходом является использование математических уравнений и условий. Например, для определения принадлежности точки к окружности, можно использовать уравнение окружности и проверить выполнение условия, что расстояние от точки до центра окружности меньше радиуса. Аналогичные методы могут быть применены и к другим геометрическим фигурам, таким как прямоугольники, эллипсы и т.д.
Помимо описанных методов, существуют также алгоритмические подходы, включающие использование компьютерных программ и алгоритмов для определения принадлежности точки к заштрихованной области. Эти подходы обычно требуют использования специализированных инструментов и программного обеспечения, которые позволяют производить сложные вычисления и анализ больших объемов данных.
| Метод | Преимущества | Недостатки |
|---|---|---|
| Разбиение на фигуры | Простота реализации, понятность результатов | Требует предварительного разбиения области, сложность с высоким числом фигур |
| Математические уравнения и условия | Гибкость, применимость к различным геометрическим фигурам | Требует знания математических формул, условий и уравнений |
| Алгоритмические подходы | Высокая точность, возможность анализа больших объемов данных | Требует специализированного программного обеспечения, сложность в реализации |
Что представляет собой заштрихованная область
Чтобы создать заштрихованную область, используются различные методы и техники, включая рисование линий с определенными интервалами, растровое заполнение шаблонами или использование специальных программ и инструментов в графических редакторах. Заштрихованная область может быть применена в различных контекстах, таких как картография, дизайн интерьера, инженерные и архитектурные чертежи, научные исследования и т.д.
Заштрихованная область служит важным средством визуальной коммуникации, позволяя легко и точно выделить определенные зоны и секторы, а также указать на принадлежность и пространственную организацию элементов на плоскости. Это визуальное обозначение помогает в понимании и анализе геометрических структур и дает возможность изображать сложные паттерны или повторяющиеся элементы даже без детальной прорисовки каждого отдельного элемента.
| Пример заштрихованной | Пример заштрихованной |
| области 1 | области 2 |
Определение положения точки на координатной плоскости
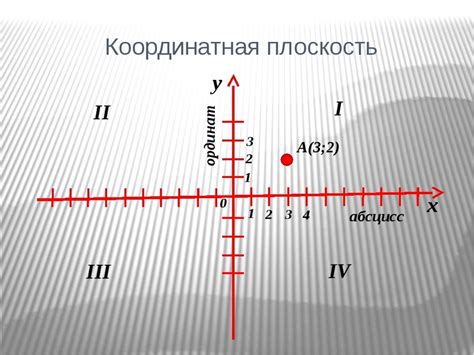
В данном разделе мы рассмотрим алгоритм определения координат точки на координатной плоскости. С помощью этого алгоритма мы сможем определить, находится ли точка в заданной области, и принять соответствующие решения на основе этого.
Для начала нам необходимо разделить координатную плоскость на четыре четверти, используя оси координат. В каждой из этих четвертей будут присутствовать определенные характеристики, которые помогут нам определить положение точки. Каждая точка на плоскости имеет две координаты - x и y, которые указывают на расположение точки относительно начала координат.
| Четверть | Характеристики |
|---|---|
| 1-я четверть | Значение x больше 0, значение y больше 0 |
| 2-я четверть | Значение x меньше 0, значение y больше 0 |
| 3-я четверть | Значение x меньше 0, значение y меньше 0 |
| 4-я четверть | Значение x больше 0, значение y меньше 0 |
Исходя из этих характеристик мы можем легко определить, в какой четверти находится заданная точка. Если точка лежит на одной из осей координат, то ее координаты будут равны 0. Таким образом, особое внимание следует обратить на такие случаи при определении положения точки.
Алгоритм для выявления принадлежности точки внутри закрашенной области
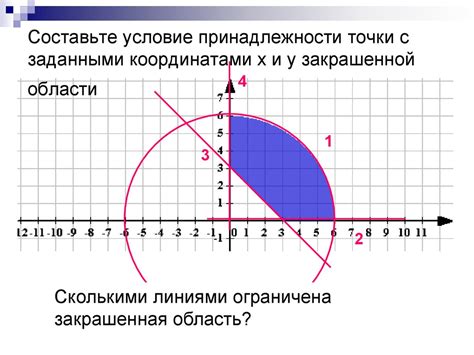
Для определения, находится ли точка внутри заданной закрашенной области, можно применить специальную формулу. Этот алгоритм позволяет быстро и надежно определить, принадлежит ли точка области или находится вне ее.
Для начала, заданная область представляется как прямоугольник, ограниченный своими координатами. Затем, координаты проверяемой точки сравниваются с координатами прямоугольника. Если точка находится внутри границ области, то она принадлежит ей, в противном случае – она находится вне области.
Чтобы определить нахождение точки внутри границ, необходимо сравнить ее координаты с координатами верхнего левого и нижнего правого угла прямоугольника. Если координаты точки лежат между соответствующими координатами углов, то точка находится внутри закрашенной области.
Для удобства организации вычислений, можно воспользоваться таблицей. Создадим таблицу с 4-мя столбцами и 2-мя строками. В первой строке разместим названия переменных (X, Y), а во второй – значения координат верхнего левого и нижнего правого углов прямоугольника. В третьем столбце можно вычислить минимальные и максимальные значения координат X и Y для углов прямоугольника.
Далее в таблице можно указать значения проверяемой точки (P), а в последнем столбце определить, принадлежит ли точка области или находится вне нее, основываясь на сравнении координат с минимальными и максимальными значениями.
Практическое применение

Использование знания о нахождении точки в заданной области может иметь практическое применение в различных сферах деятельности. Например, в географии оно может помочь в определении принадлежности конкретной территории к определенному региону или стране. В медицине знание о точках нахождения органов или нервных окончаний может быть полезным при проведении различных процедур или операций. В архитектуре и дизайне определение точки в заданных границах может помочь в создании гармоничных и эстетически приятных композиций.
Практическое использование этой информации может быть полезным также в финансовых расчетах, например, при определении зон риска или прогнозировании поведения цен на финансовых рынках. Кроме того, знание о нахождении точки в заданной области может пригодиться в информационной безопасности при определении уязвимых мест в сетевой инфраструктуре или при построении системы обнаружения аномалий.
Важно помнить, что знание о нахождении точки в заданной области может быть полезным в различных областях деятельности и представляет собой мощный инструмент для анализа и принятия решений. Это позволяет определить принадлежность или отношение чего-либо к определенной категории, заштрихованной области или географической зоне, что может быть полезно для достижения конкретных целей и улучшения результатов в различных сферах деятельности.
Примеры практического решения задачи
В этом разделе мы рассмотрим несколько примеров решения задачи по определению принадлежности точки к заштрихованной области. Каждый пример представлен в виде последовательности шагов, которые позволят нам достичь результата.
Пример 1:
- Начнем с построения геометрической модели данной области, описывающей форму и положение штрихованной области на плоскости.
- Определим уравнение кривых, ограничивающих заштрихованную область.
- Решим систему уравнений, чтобы найти точки пересечения кривых.
- Проверим, находится ли исследуемая точка внутри границ области, используя метод геометрического анализа.
- Выведем результат - точка либо принадлежит заштрихованной области, либо находится вне ее.
Пример 2:
- Используем метод подсчета количества пересечений луча сегмента, выходящего из точки, и каждой границы заштрихованной области.
- Зададим луч и проведем его из исследуемой точки в произвольном направлении.
- Подсчитаем количество пересечений луча с каждой границей области.
- Определим, является ли количество пересечений четным или нечетным.
- На основе результата определим принадлежность точки заштрихованной области.
Примеры решения задачи по определению принадлежности точки заштрихованной области позволяют использовать различные методы и подходы, в зависимости от особенностей задачи и доступных инструментов.
Вопрос-ответ

Как определить, находится ли точка в заштрихованной области?
Определение нахождения точки в заштрихованной области может быть выполнено путем использования метода графического анализа. Этот метод основывается на сравнении координат точки с уравнениями границ области. Если точка удовлетворяет уравнениям границ области, то она находится внутри заштрихованной области.
Какие инструменты можно использовать для определения нахождения точки в заштрихованной области?
Для определения нахождения точки в заштрихованной области можно использовать графический калькулятор или компьютерную программу, которая позволяет визуализировать заштрихованную область и вводить координаты точки. Также можно использовать графический метод, при котором на графике строятся границы области и проверяется, находится ли точка внутри этих границ.
Какие примеры областей могут быть заштрихованы?
Области, которые могут быть заштрихованы, зависят от контекста и задачи, для которой требуется определить нахождение точки. Например, могут быть заштрихованы области треугольников, прямоугольников, окружностей и других геометрических фигур. Также могут быть заштрихованы области, определенные неравенствами или сложными функциями.
Какая точность можно достичь при определении нахождения точки в заштрихованной области?
Точность определения нахождения точки в заштрихованной области зависит от используемых инструментов и методов. С использованием графического калькулятора или компьютерной программы можно достичь высокой точности, так как они позволяют работать с большим количеством координат и сложными функциями. Однако при использовании графического метода точность будет зависеть от масштаба и качества графика, а также от умения определить границы области.



