Анализ точек, принадлежащих окружности, является важной задачей в геометрии и программировании. Существует несколько методов, позволяющих определить, лежит ли точка на окружности или внутри/снаружи нее.
Одним из популярных методов является использование уравнения окружности и координат точки для проверки их соответствия. Этот метод позволяет с высокой точностью определить принадлежность точки к окружности.
В этой статье мы рассмотрим различные подходы и приведем примеры задач, где необходимо проверить, принадлежит ли точка заданной окружности или нет.
Что такое проверка принадлежности точки окружности?

Простой способ проверить, принадлежит ли точка окружности, состоит в том, что расстояние от центра окружности до этой точки должно быть равно радиусу окружности.
Геометрическое определение условий

Для проверки принадлежности точки M окружности с центром в точке O и радиусом R можно использовать геометрическое определение. Точка M принадлежит окружности, если расстояние от точки M до центра O равно радиусу R.
Для вычисления расстояния между точками M и O можно использовать формулу расстояния между двумя точками в прямоугольной системе координат:
| AB | = | √((x2 - x1)2 + (y2-y1)2) |
Где (x1, y1) - координаты центра O, а (x2, y2) - координаты точки M. Если полученное расстояние равно радиусу R, то точка M лежит на окружности, иначе она находится вне нее.
Метод с использованием уравнения окружности
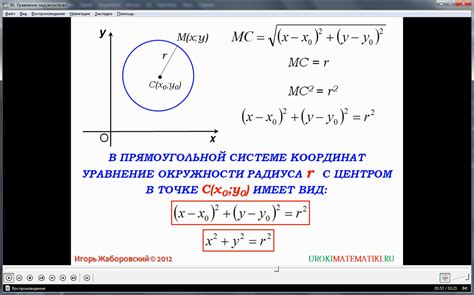
Уравнение окружности имеет вид: $(x - a)^2 + (y - b)^2 = r^2$.
Для проверки принадлежности точки к окружности, подставляем координаты точки в уравнение окружности и проверяем равенство.
Пример:
- Дана окружность с центром в $(2, 3)$ и радиусом $5$.
- Проверим принадлежность точки $(4, 1)$ к этой окружности.
- Подставляем $x=4$ и $y=1$ в уравнение окружности: $(4 - 2)^2 + (1 - 3)^2 = 2^2 + (-2)^2 = 4 + 4 = 8 eq 5^2$.
- Точка $(4, 1)$ не принадлежит окружности.
Аналитический подход с координатами точки
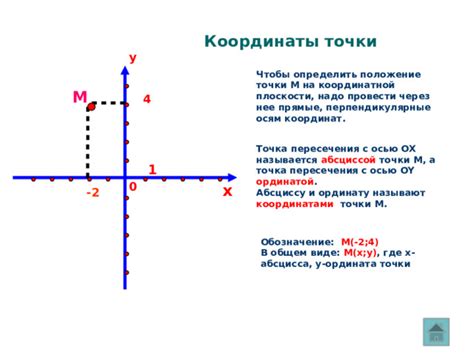
Для проверки принадлежности точки окружности можно использовать аналитический подход, основанный на координатах точки и уравнении окружности.
Шаги аналитической проверки:
- Записать уравнение окружности в виде (x-a)^2 + (y-b)^2 = r^2, где (a,b) - координаты центра окружности, r - радиус.
- Подставить координаты точки (x,y) в уравнение окружности.
- Если равенство выполнено, то точка принадлежит окружности; если не выполнено, то точка не принадлежит окружности.
Пример: Уравнение окружности (x-2)^2 + (y-3)^2 = 25. Координаты точки (4,1).
Точка (4,1): (4-2)^2 + (1-3)^2 = 4 + 4 = 8 ≠ 25, поэтому точка (4,1) не принадлежит окружности.
Графический способ проверки принадлежности
Для графической проверки принадлежности точки окружности можно использовать метод построения окружности на координатной плоскости и нанесения точки на этот график.
Шаги проверки:
| Шаг | Действие |
|---|---|
| 1 | Постройте окружность с центром в точке (x0, y0) и радиусом r. |
| 2 | Нанесите точку (x, y) на график. |
| 3 | Проверьте, лежит ли точка внутри окружности (находится внутри границы) или снаружи (вне границ). |
Если точка (x, y) лежит на окружности, то она принадлежит окружности, а если точка внутри или снаружи, то она не принадлежит.
Примеры расчетов с известными значениями

Давайте рассмотрим несколько примеров расчетов, чтобы увидеть, как проверить принадлежность точки окружности на практике.
Пример 1:
Дана окружность с радиусом 5 и центром в точке (0,0). Проверим, принадлежит ли точка (3,4) этой окружности.
Расстояние от центра окружности до точки (3,4) вычисляется по формуле √((x1-x2)^2 + (y1-y2)^2).
В нашем случае: x1 = 0, y1 = 0, x2 = 3, y2 = 4.
Расстояние равно √((0-3)^2 + (0-4)^2) = √(9 + 16) = √25 = 5.
Так как расстояние равно радиусу окружности, точка (3,4) принадлежит окружности.
Пример 2:
Дана окружность с радиусом 2 и центром в точке (-3,1). Проверим, принадлежит ли точка (0,1) этой окружности.
Аналогично предыдущему примеру, вычислим расстояние от центра до точки (0,1).
В нашем случае: x1 = -3, y1 = 1, x2 = 0, y2 = 1.
Расстояние равно √((-3-0)^2 + (1-1)^2) = √(9 + 0) = √9 = 3.
Так как расстояние не равно радиусу окружности, точка (0,1) не принадлежит окружности.
Интерактивные задачи и решения
Попробуйте свои силы в решении следующих задач:
1. Дана окружность с центром в точке (5, 3) и радиусом 7. Проверьте, принадлежит ли точка (8, 5) этой окружности.
2. Определите, лежит ли точка (2, 4) на окружности с центром в точке (-1, -2) и радиусом 5.
3. Проверьте, принадлежит ли точка (0, 0) окружности с центром в точке (3, 4) и радиусом 5.
Приведем пример решения одной из задач:
Решение задачи 1:
Для точки (8, 5) вычисляем расстояние до центра окружности: √((8-5)^2 + (5-3)^2) = √(3^2 + 2^2) = √13. Данное расстояние равно радиусу окружности 7, поэтому точка (8, 5) принадлежит окружности.
Практическое применение в различных областях
В области инженерии данный метод используется для решения задач машинного зрения, проектирования и моделирования объектов, а также в навигационных системах. Зная координаты центра окружности и ее радиус, можно легко определить, находится ли точка внутри или снаружи этой окружности. Это позволяет упростить многие технические расчеты и задачи, связанные с пространственными координатами.
Вопрос-ответ

Какие методы можно использовать для проверки принадлежности точки окружности?
Для проверки принадлежности точки окружности можно использовать различные методы, такие как вычисление расстояния от центра окружности до точки и сравнение с радиусом, использование уравнения окружности в общем виде или параметрического уравнения окружности, а также использование свойства, что точка на окружности расположена на равном расстоянии от центра окружности. Каждый из этих методов позволяет эффективно проверить принадлежность точки заданной окружности.
Можете привести пример проверки принадлежности точки окружности с использованием уравнения окружности в общем виде?
Конечно! Предположим, у нас есть окружность с центром в точке (3,4) и радиусом 5. Чтобы проверить принадлежность точки (1,2) данной окружности, мы можем использовать уравнение окружности в общем виде: (x - 3)^2 + (y - 4)^2 = 5^2. Подставляем координаты точки (1,2) в это уравнение: (1 - 3)^2 + (2 - 4)^2 = 4 + 4 = 8, что не равно 25 (радиус окружности в квадрате), следовательно, точка (1,2) не принадлежит данной окружности.



